Théorème De L'énergie Mécanique

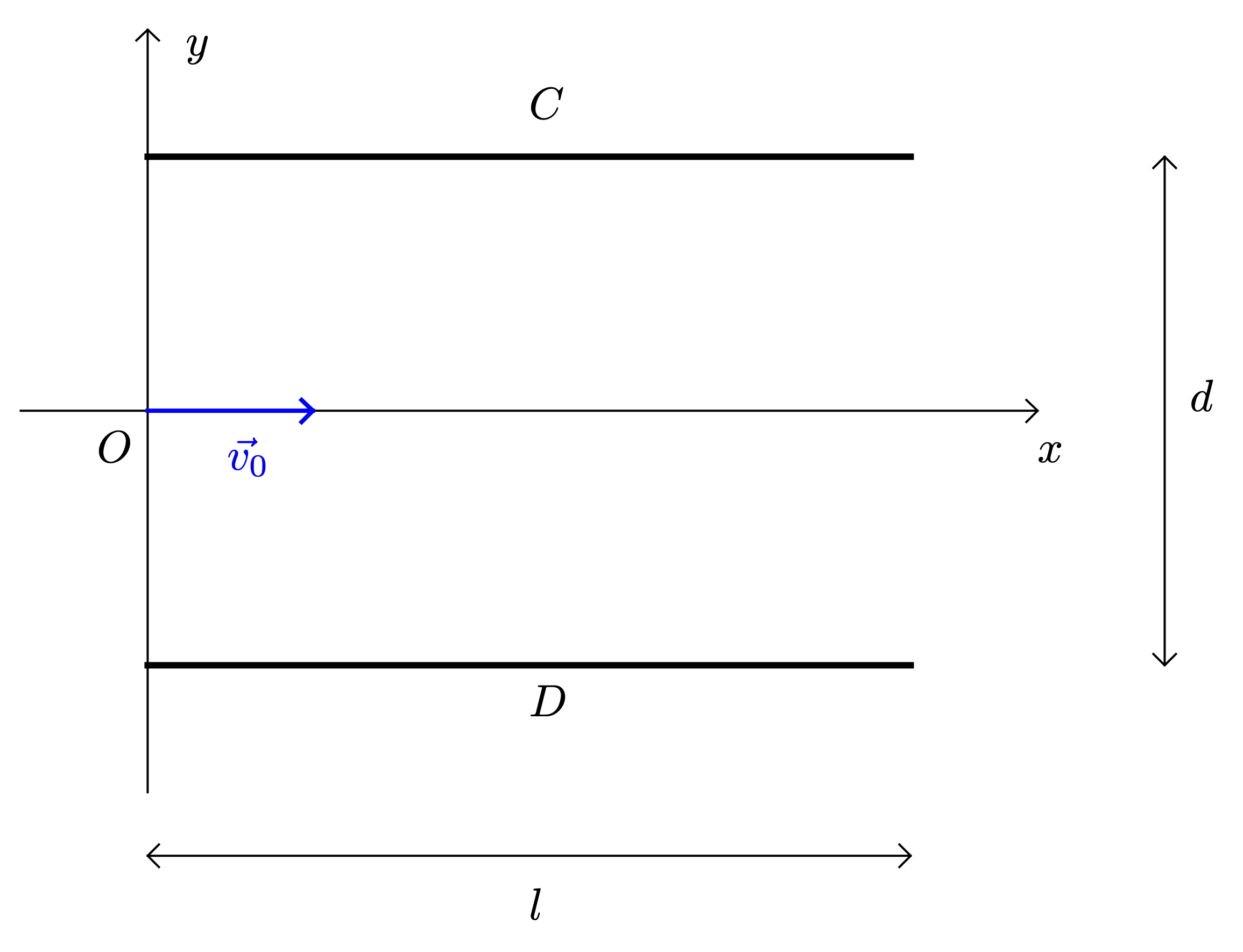
Une particule $\alpha$ (noyau d’hélium : $\ce{^{4}_{2}He}$) arrive au point $O$ dans un condensateur plan avec une vitesse $\vec{v_0}$ de direction parallèle aux armatures $C$ et $D$ du condensateur. Une tension constante $U$ est appliquée entre ces deux armatures longues de $l = \pu{5,00 cm}$ et distantes de $d = \pu{4,00 cm}$. Données On négligera le poids de la particule $\alpha$ devant la force électrostatique. On rappelle que pour un condensateur plan : $E = \dfrac{U}{d}$. [Lire]

Le problème posé par la nature des « rayons cathodiques » à la fin du XIXème siècle fut résolu en 1897 par l’Anglais J.J. Thomson : il s’agissait de particules chargées négativement baptisées par la suite « électrons ». La découverte de l’électron valut à Thomson le prix Nobel de physique en 1906. Le défi pour les scientifiques de l’époque fut alors de déterminer les caractéristiques de cette particule : sa charge électrique et sa masse. [Lire]

Champ électrique Force de Coulomb Force de Coulomb Lorsque deux charges électriques immobiles se trouvent aux points $M_1$ et $M_2$ de l’espace, on modélise l’action de la charge $q_1$ sur la charge $q_2$ par une force, la force de Coulomb, dont les caractéristiques sont : $$ \vec{F}_{q_1 / q_2} = \begin{cases} \textbf{Point d’application :} & M_2\cr \textbf{Direction :} & \text{droite } (M_1 M_2)\cr \textbf{Sens :} & \text{dépend des signes des charges}\cr \textbf{Valeur :} & F_{q_1 / q_2} = k\, \dfrac{\lvert q_1 \cdot q_2 \rvert}{d^2} \end{cases}$$ [Lire]

Champ de pesanteur Notion de champ En physique, un champ est la valeur, en chaque point de l’espace, d’une grandeur physique. Cette grandeur physique peut être scalaire (pression, température, etc.) ou vectorielle (vitesse, champ électrique, etc.). Les physiciens pensent que toutes les interactions sont assurées par des champs (gravitationnel, électromagnétique, nucléaire, etc). Un corps $A$ suscite l’apparition dans l’espace d’un champ de forces qui se manifeste par des forces appliquées à n’importe quel objet $B$ placé en ce point (et sensible à cette interaction bien sûr). [Lire]