Champ électrique
Force de Coulomb
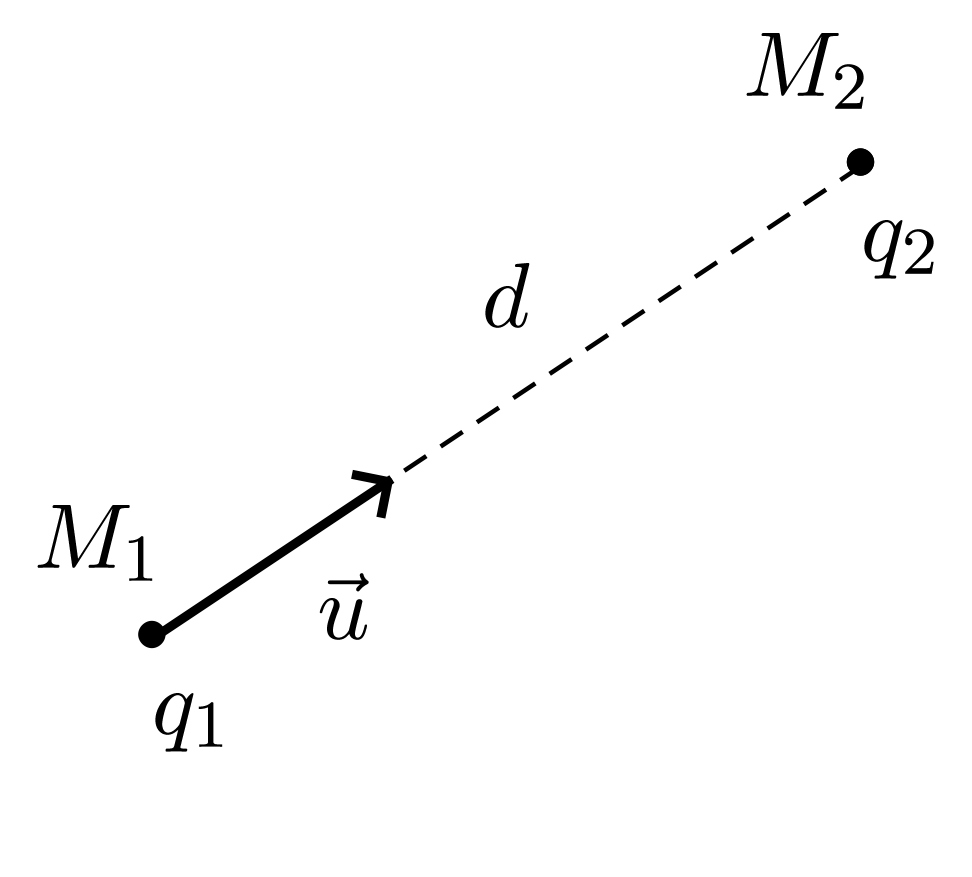
Force de Coulomb
Lorsque deux charges électriques immobiles se trouvent aux points $M_1$ et $M_2$ de l’espace, on modélise l’action de la charge $q_1$ sur la charge $q_2$ par une force, la force de Coulomb, dont les caractéristiques sont :
$$ \vec{F}_{q_1 / q_2} = \begin{cases} \textbf{Point d’application :} & M_2\cr \textbf{Direction :} & \text{droite } (M_1 M_2)\cr \textbf{Sens :} & \text{dépend des signes des charges}\cr \textbf{Valeur :} & F_{q_1 / q_2} = k\, \dfrac{\lvert q_1 \cdot q_2 \rvert}{d^2} \end{cases}$$
Principe des actions réciproques
$$ \vec{F}_{q_1 / q_2} = - \vec{F}_{q_2 / q_1} $$
Expression vectorielle
On peut exprimer de façon plus condensée la force de Coulomb en utilisant le vecteur unitaire $\vec{u}$ de la droite $(M_1 M_2)$ : $$ \vec{F}_{q_1 / q_2} = k\, \dfrac{q_1 \cdot q_2}{d^2}\, \vec{u} $$
-
Si $q_1$ et $q_2$ sont de même signe, $q_1 \cdot q_2 > 0$, $\vec{F}_{q_1 / q_2}$ et $\vec{u}$ sont colinéaires de même sens : l’interaction est répulsive ;
-
Si $q_1$ et $q_2$ sont de signes opposés, $q_1 \cdot q_2 < 0$, $\vec{F}_{q_1 / q_2}$ et $\vec{u}$ sont colinéaires de sens opposés : l’interaction est attractive.
Qu’appelle-t-on « champ électrique » ?
-
Si on remplace, au point $M_2$, la charge électrique $q_2$ par une charge électrique $q_3$, cette dernière est soumise de la part de la particule $q_1$ une action modélisée par la force : $\vec{F}_{q_1 / q_3} = k\, \dfrac{q_1 \cdot q_3}{d^2}\, \vec{u}$ ;
-
Si on remplace, au point $M_2$, la charge électrique $q_3$ par une charge électrique $q_4$, cette dernière est soumise de la part de la particule $q_1$ une action modélisée par la force : $\vec{F}_{q_1 / q_4} = k\, \dfrac{q_1 \cdot q_4}{d^2}\, \vec{u}$ ;
Champ électrique
Quelle que soit la charge qui subit l’action de la charge $q_1$, on constate que : $$ \dfrac{\vec{F}_{q_1 / q_2}}{q_2} = \dfrac{\vec{F}_{q_1 / q_3}}{q_3} = \dfrac{\vec{F}_{q_1 / q_4}}{q_4} = \cdots = k\, \dfrac{q_1}{d^2}\, \vec{u} = \vec{E} (M_2) $$ $\vec{E} (M_2)$, champ électrique au point $M_2$ créé par $q_1$, représente la force électrique que subirait une charge électrique de valeur $q = 1 \text{C}$, placée au point $M_2$, de la part de la charge $q_1$.
La présence de la charge $q_1$ au point $M_1$ « communique » à tout point de l’espace la propriété suivante :
Relation entre la force électrique et le champ électrique en un point
Toute charge électrique $q$ placée en un point $M$ de l’espace subit de la part de $q_1$ la force : $$ \vec{F}_{el} = q \vec{E} (M) $$ où $\vec{E} (M)$ est le champ électrique créé par la charge $q_1$, au point $M$.
Remarque
En un point de l’espace les champs électriques créés par différentes charges s’additionnent.
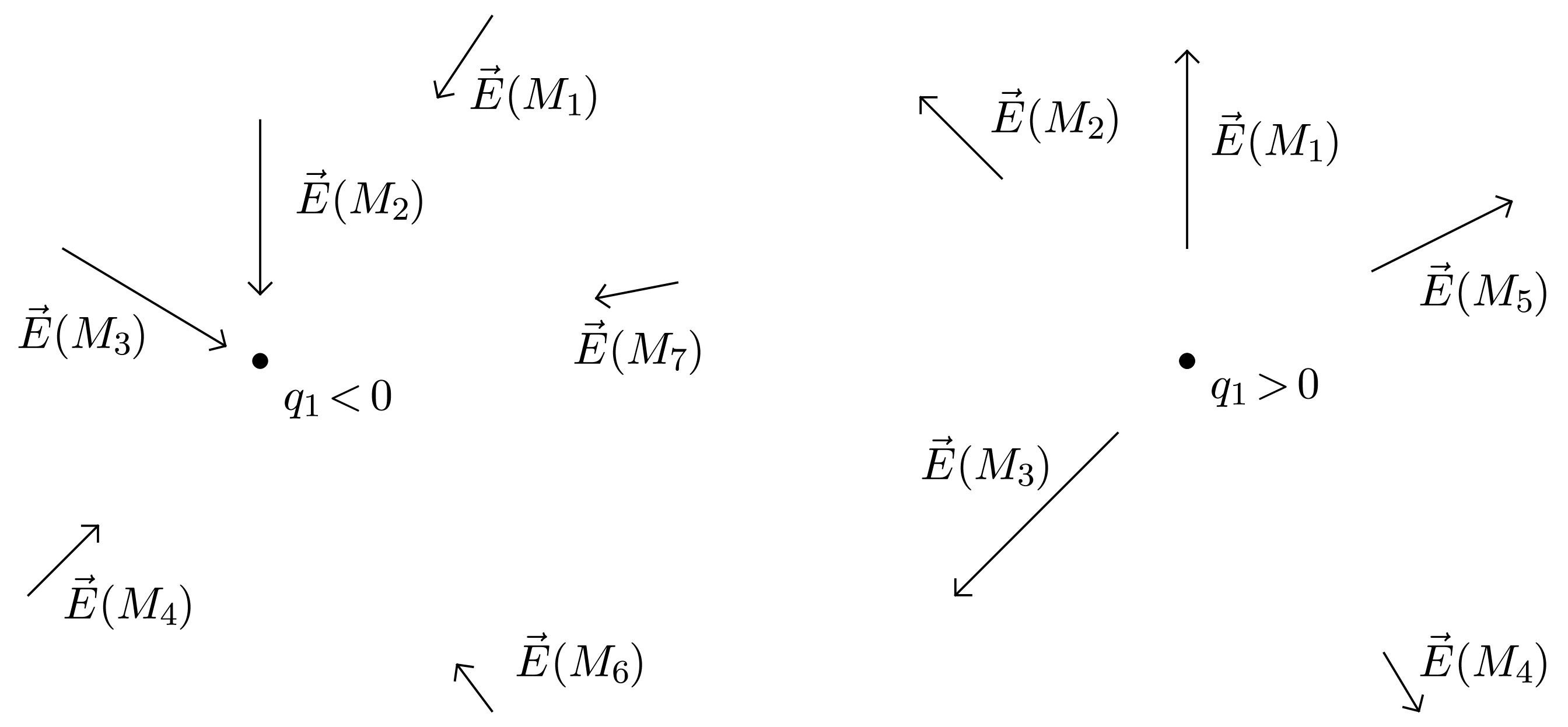
-
La direction du champ électrique dépend du point $M$ considéré ;
-
La valeur du champ électrique varie comme l’inverse du carré de la distance à la charge $q_1$.
Comment créer un champ électrique uniforme ?
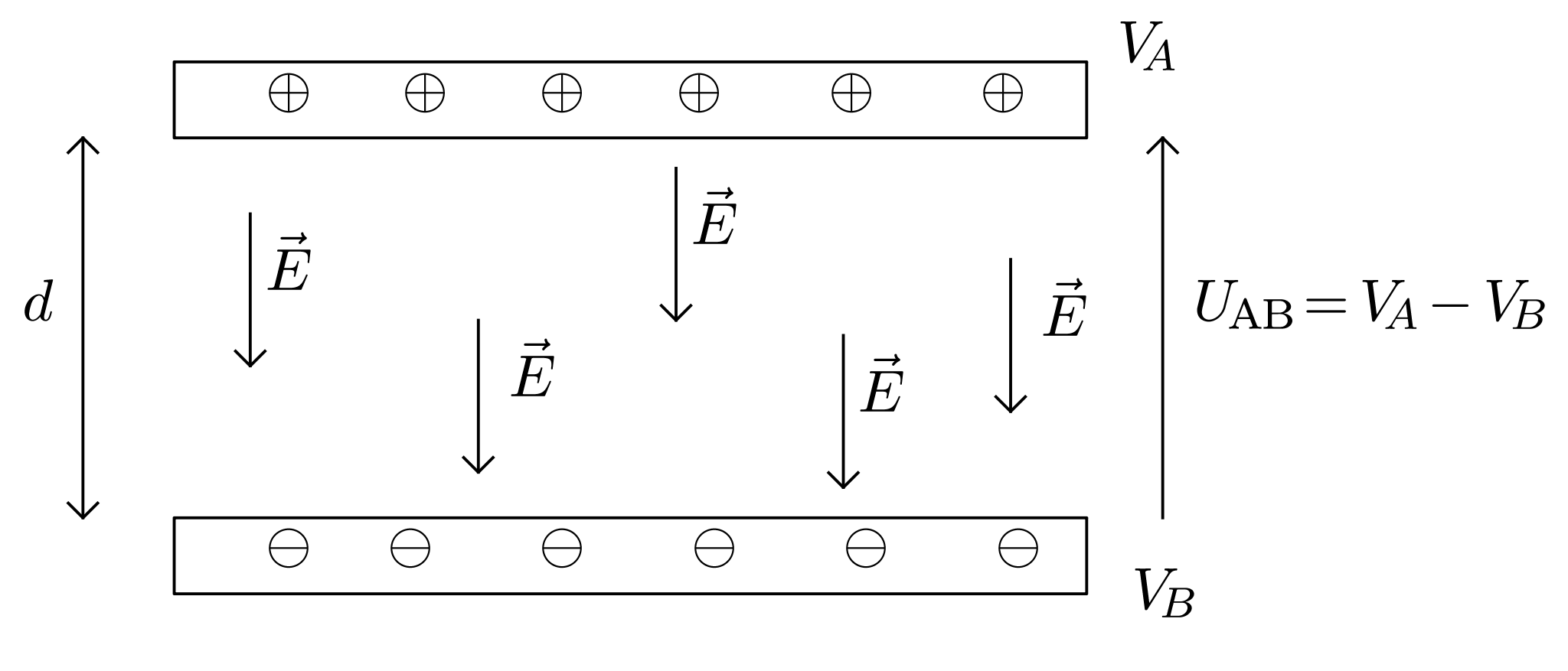
Relation entre la tension électrique et le champ électrique
Une tension électrique $U$ entre les deux armatures conductrices planes d’un condensateur, séparées par une distance $d$, crée un champ électrique uniforme entre ces deux armatures, dirigé de l’armature positive vers l’armature négative et ayant pour valeur :
$$ E = \dfrac{U_{AB}}{d} = \dfrac{V_A - V_B}{d} \tag{1}\label{eq:1} $$
L’unité du champ électrique est donc le volt par mètre (symbole : $\pu{V/m}$).
Rappel
On appelle tension électrique la différence de potentiel entre deux points de l’espace.
Énergie potentielle électrique
Tout comme une masse possède une énergie potentielle de pesanteur car elle se trouve à une certaine altitude par rapport à la Terre, une charge possède une énergie potentielle électrique car elle se trouve à un certain potentiel électrique.
Rappel : Comment déterminer l’expression de l’énergie potentielle associée à une interaction ?
- Vérifier que la force $\vec{F}_{el}$ qui modélise l’interaction est conservative.
- Déterminer l’expression du travail qu’effectuerait un opérateur déplaçant le système (ici une charge électrique) dans le champ modélisant l’interaction, à vitesse nulle.
- L’énergie fournie par l’opérateur est stockée par le système : $$ \Delta E_p = W_{AB}(\vec{F}_{op}) = - W_{AB}(\vec{F}_{el}) $$ puisqu’à chaque instant $\vec{F}_{op} = -\vec{F}_{el}$.
La force électrique créée par un champ électrique uniforme est conservative
Réponse
Le travail entre deux points d’une force conservative ne dépend pas du chemin suivi par le système sur lequel s’applique la force conservative. Ce travail ne dépend que des caractéristiques des deux points.
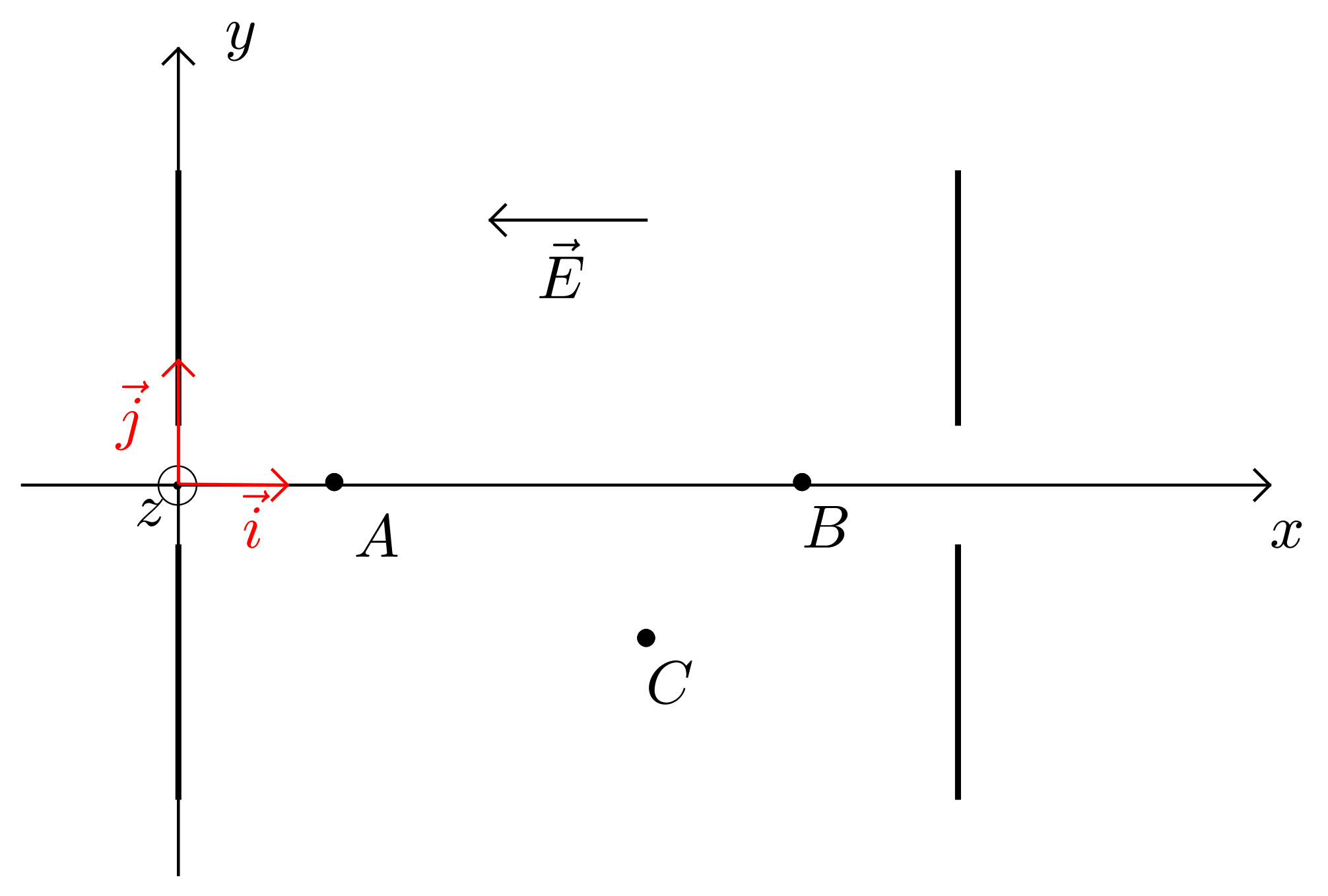
Une particule de charge électrique $q$ se déplace du point $A$, où règne le potentiel électrique $V_A$, au point $B$, où règne le potentiel électrique $V_B$. On souhaite exprimer le travail de la force électrique qui s’applique sur cette particule lorsqu’elle se déplace du point $A$ au point $B$.
Deux trajets sont envisagés $A \longrightarrow B$ et $A \longrightarrow C \longrightarrow B $.
Les coordonnées des points $A$, $B$ et $C$ sont les suivantes : $(x_A, 0, 0)$, $(x_B, 0, 0)$, $(x_C, y_C, O)$. Les composantes du vecteur $\vec{E}$ sont $(-E, 0, 0)$.
Réponse
Puisque le force électrique est une force constante, $$W_{AB}(\vec{F}_{el}) = \vec{F}_{el} \cdot \overrightarrow{AB} = q\, \vec{E} \cdot \overrightarrow{AB} = q\, (-E) \vec{i} \cdot (x_B - x_A) \vec{i} = -q E (x_B - x_A) $$
Réponse
Puisque le force électrique est une force constante, $$ W_{AB}(\vec{F}_{el}) = W_{AC}(\vec{F}_{el}) + W_{CB}(\vec{F}_{el}) = \vec{F}_{el} \cdot \overrightarrow{AC} + \vec{F}_{el} \cdot \overrightarrow{CB} $$
$$ W_{AB}(\vec{F}_{el}) = \vec{F}_{el} \cdot (\overrightarrow{AC} + \overrightarrow{CB}) = \vec{F}_{el} \cdot \overrightarrow{AB} $$
On retrouve la même expression du travail, pour la force électrique, quel que soit le chemin suivi.
Travail d’un opérateur déplaçant une charge dans un champ électrique uniforme
Réponse
Puisque le force électrique est une force constante, $$ W_{AB}(\vec{F}_{op}) = \vec{F}_{op} \cdot \overrightarrow{AB} = - \vec{F}_{el} \cdot \overrightarrow{AB} $$ puisqu’à chaque instant $\vec{F}_{op} + \vec{F}_{el} = \vec{0}$.
Donc
$$
W_{AB}(\vec{F}_{op}) = -q\, \vec{E} \cdot \overrightarrow{AB} = -q\, (-E) \vec{i} \cdot (x_B - x_A) \vec{i} = q E (x_B - x_A)
$$
La relation $\eqref{eq:1}$ indique que $(x_A - x_B) = E U_{AB} = E (V_A - V_B)$, donc $$ W_{AB}(\vec{F}_{op}) = q (V_B - V_A) \tag{2}\label{eq:2} $$
Expression de l’énergie potentielle électrique
Réponse
L’énergie transférée par l’opérateur à la charge électrique fait varier son énergie potentielle électrique : $$ \Delta E_{Pel\;A \to B} = W_{AB}(\vec{F}_{op}) = q (V_B - V_A) \tag{3}\label{eq:3} $$ Comme $\Delta E_{Pel\;A \to B} = E_{Pel}(B) - E_{Pel}(A) = q (V_B - V_A)$ on peut en déduire que, de façon générale, l’énergie potentielle électrique a pour expression : $$ E_{Pel}(M) = q V_M + \text{cste} $$
Rappels
Seules les variations d’énergies ont un sens physique. Les énergies potentielles d’interactions sont définies à une constante additive près.
Lorsqu’on calcule une variation d’énergie potentielle d’interaction l’influence du choix de la constante additive disparaît.
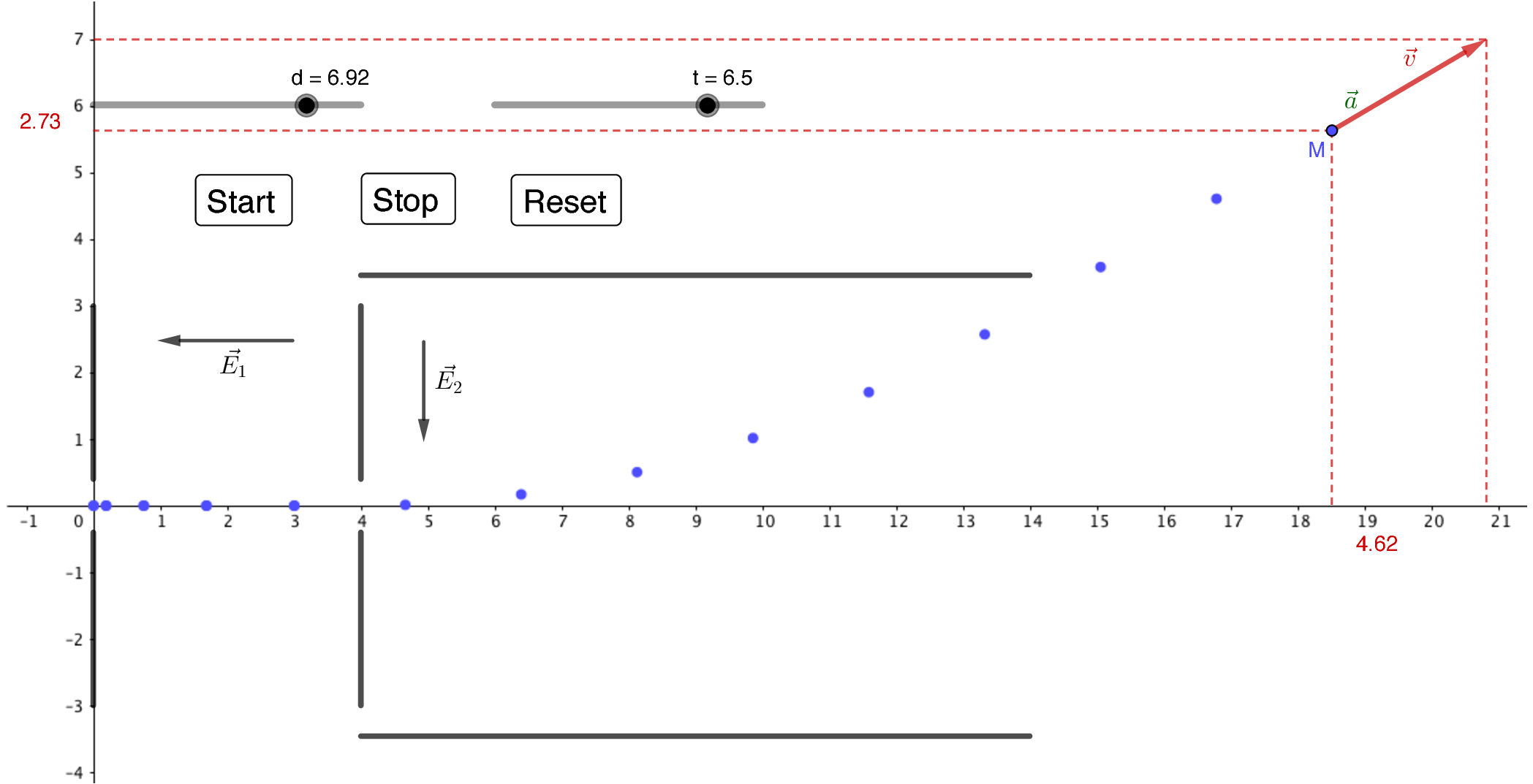
Mouvement d’un électron dans un oscilloscope
Première phase : accélération dans un canon à électrons
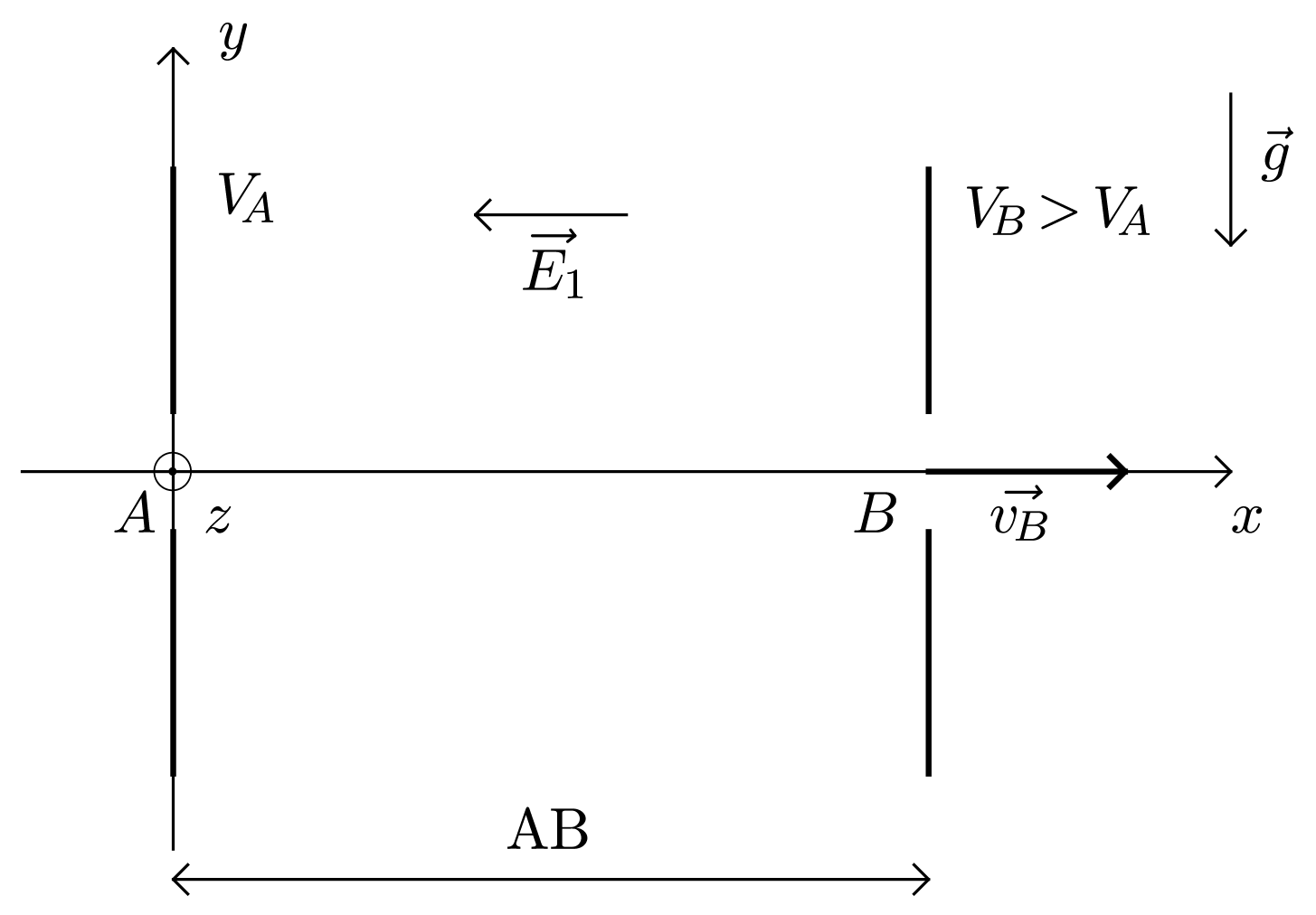
Un électron est produit avec une vitesse quasi-nulle au point $A$ entrée d’une zone de l’espace où règne un champ électrique $\vec{E}_1$ créé par deux armatures conductrices planes parallèles distantes de $AB$ et le champ de pesanteur $\vec{g}$.
On cherche à déterminer les équations horaire du mouvement de l’électron et plus particulièrement sa vitesse $\vec{v}_B$ au point $B$.
- Données
- $e = \pu{1,6e- 19 C}$ ; $m_e = \pu{9,11e-31 kg}$ ; $AB = \pu{3 cm}$ ; $E_1 = \pu{6,0e4 V.m-1}$.
Détermination des équations horaires du mouvement de l’électron — Lois de Newton
-
Déterminer à quelles interactions est soumis l’électron et modéliser chacune d’elles.
-
Écrire la seconde loi de Newton décrivant le mouvement de l’électron.
Réponse
-
Système : {électron}
-
Interactions :
-
Système - champ de pesanteur, modélisée par le poids : $\vec{P} = m_e\, \vec{g}$
-
Système - champ électrique, modélisée par la force électrique : $\vec{F}_1 = - e\, \vec{E}_1$
-
-
Référentiel : {terrestre supposé galiléen}
-
Schématisation : (pas à l’échelle)
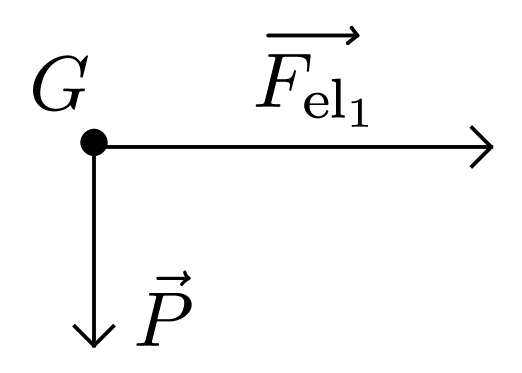
-
Deuxième loi de Newton : puisque la masse $m_e$ d’un électron est constante, on peut écrire $$ m_e \vec{a}_1 = \vec{P} + \vec{F}_1 = m_e\, \vec{g} - e\, \vec{E}_1 $$
-
Comparer les valeurs de la force électrique et du poids.
-
Modifier la deuxième loi de Newton à partir du résultat de la question précédente.
Réponse
-
Comparaison des valeurs du poids et de la force électrique : $$ \dfrac{\Vert - e\, \vec{E}_1 \Vert}{\Vert m_e\, \vec{g} \Vert} \simeq \dfrac{\pu{1e-19 C} \times \pu{1e5 V.m-1}}{\pu{1e-30 kg} \times \pu{10 N.m-1}} = \dfrac{10^{- 14}}{10^{- 29}} = 10^{15}$$ La valeur de la force électrique est donc $10^{15}$ fois plus élevée que celle du poids !
On peut donc considérer que le poids communique une accélération à l’électron négligeable comparée à celle que la force électrique lui communique. -
Deuxième loi de Newton (bis) : $$ m_e\, \vec{a}_1 = - e\, \vec{E}_1 $$ ou $$ \boxed{ \vec{a}_1 = - \dfrac{e}{m_e} \vec{E}_1 } $$
Réponse
Le mouvement du système est uniformément accéléré.
Réponse
-
Repère associé au système d’axes $(x’ x)$, $(y’ y)$, $(z’ z)$ : $(A ; \vec{i}, \vec{j}, \vec{k})$ :
-
Projections des conditions initiales et des grandeurs apparaissant dans la relation de Newton : $$\overrightarrow{AM} (0) = \left(\begin{array}{c} 0\cr 0\cr 0 \end{array}\right) \text{ ; } \vec{v}_A = \vec{v}_1 (0) = \left(\begin{array}{c} 0\cr 0\cr 0 \end{array}\right) \text{ ; } \vec{a}_1 = \left(\begin{array}{c} a_{1 x}\cr a_{1 y}\cr a_{1 z} \end{array}\right) \text{ ; } \vec{E}_1 = \left(\begin{array}{c} - E_1\cr 0\cr 0 \end{array}\right)$$
-
Projection de la deuxième loi de Newton : $$ \left(\begin{array}{c} a_{1 x}\cr a_{1 y}\cr a_{1 z} \end{array}\right) = - \dfrac{e}{m_e} \left(\begin{array}{c} -E_1\cr 0\cr 0 \end{array}\right) = \left(\begin{array}{c} \dfrac{eE_1}{m_e}\cr 0\cr 0 \end{array}\right) $$ donc $$ \boxed{ \begin{cases} a_{1 x} &= \dfrac{eE_1}{m_e}\cr a_{1 y} &= 0\cr a_{1 z} &= 0 \end{cases} } $$
Le mouvement est donc uniformément accéléré selon l’axe $(A x)$. Il n’est pas possible de conclure quant à la forme du mouvement selon les axes $(A y)$ et $(A z)$ : mouvements uniformes ou pas de mouvement.
Réponse
Composantes de la vitesse : $$ \begin{cases} a_{1 x} &= \dfrac{\mathrm{d}v_{1 x}}{\mathrm{dt}} = \dfrac{eE_1}{m_e}\cr a_{1 x} &= \dfrac{\mathrm{d}v_{1 y}}{\mathrm{dt}} = 0\cr a_{1 z} &= \dfrac{\mathrm{d}v_{1 z}}{\mathrm{dt}} = 0 \end{cases} $$ donc $$ \begin{cases} v_{1 x} (t) &= \dfrac{eE_1}{m_e} t + A\cr v_{1 y} (t) &= B\cr v_{1 z} (t) &= C \end{cases} $$ Conditions initiales pour la vitesse : $$ \begin{cases} v_{1 x} (0) = A = 0\cr v_{1 y} (0) = B = 0\cr v_{1 z} (0) = C = 0 \end{cases} $$ Finalement $$ \boxed{ \begin{cases} v_{1 x} (t) = \frac{eE_1}{m_e} t\cr v_{1 y} (t) = 0\cr v_{1 z} (t) = 0 \end{cases} } $$ Il n’y a aucun mouvement selon les axes $(A y)$ et $(A z)$.
Réponse
Composantes du vecteur position :
$$ \begin{cases} v_{1 x} (t) &= \dfrac{\mathrm{d}x_1}{\mathrm{dt}} = \dfrac{eE_1}{m_e} t\cr v_{1 y} (t) &= \dfrac{\mathrm{d}y_1}{\mathrm{dt}} = 0\cr v_{1 z} (t) &= \dfrac{\mathrm{d}z_1}{\mathrm{dt}} = 0 \end{cases} $$ donc $$ \begin{cases} x_1 (t) &= \dfrac{1}{2}\, \dfrac{eE_1}{m_e} t^2 + D\cr y_1 (t) &= E\cr z_1 (t) &= F \end{cases} $$ Conditions initiales pour la position : $$ \begin{cases} x_1 (0) &= D = 0\cr y_1 (0) &= E = 0\cr z_1 (0) &= F = 0 \end{cases} $$ Finalement $$ \boxed{ \begin{cases} x_1 (t) &= \dfrac{1}{2}\, \dfrac{eE_1}{m_e}\, t^2\cr y_1 (t) &= 0\cr z_1 (t) &= 0 \end{cases} } $$
Détermination de la valeur de la vitesse au point $B$ — Lois de Newton
Réponse
Comme toujours il est impossible de répondre directement à cette question à partir des équations horaires qui utilisent le paramètre temps, il faut se poser à la question suivante : à quelle date l’électron parvient-il en $B$ ?
Si on note $t_B$ la date à laquelle l’électron parvient en $B$, alors $$ x_1 (t_B) = \dfrac{1}{2}\, \dfrac{eE_1}{m_e}\, t_B^2 = AB \Leftrightarrow \boxed{ t_B = \sqrt{\dfrac{2 m_e\, AB }{eE_1}} } $$ et $$ v_{1 B} = v_{1 x} (t_B) = \dfrac{eE_1}{m_e} \sqrt{\dfrac{2 m_e \, AB }{eE_1}} $$ finalement $$ \boxed{ v_{1 B} = \sqrt{\dfrac{2eE_1\, AB }{m_e}} } $$
A.N. : $t_B = \pu{2,4e-9 s}$ ; $v_{1 B} =\pu{2,5e7 m.s-1}$.
Détermination de la valeur de la vitesse au point $B$ — Théorème de l’énergie mécanique
Réponse
La seule force qui s’applique sur l’électron est la force électrique, force conservative ; l’énergie mécanique de l’électron se conserve donc.
- Au point $A$ : $E_M(A) = E_C(A) + E_{Pel}(A) = -e V_A + \text{cste}$ puisque l’électron est produit sans vitesse.
- Au point $B$ : $E_M(B) = E_C(B) + E_{Pel}(B) = \dfrac{1}{2}\, m_e v_{1 B}^2 - e V_B + \text{cste}$
- L’énergie mécanique se conserve : $\Delta E_M = 0 \iff E_M(A) = E_M(B)$ donc $$ -e V_A + \text{cste} = \dfrac{1}{2}\, m_e v_{1 B}^2 - e V_B + \text{cste} $$ et $$ \boxed{ v_{1 B} = \sqrt{ \dfrac{2 e}{m_e}\, (V_B - V_A) } } $$ Ce résultat est-il identique au précédent ? À partir du schéma, on peut écrire $$ E_1 = \dfrac{V_B - V_A}{AB}$$ donc le résultat précédent s’écrit aussi $$ \boxed{ v_{1 B} = \sqrt{ \dfrac{2 e E_1\, AB}{m_e}} } $$
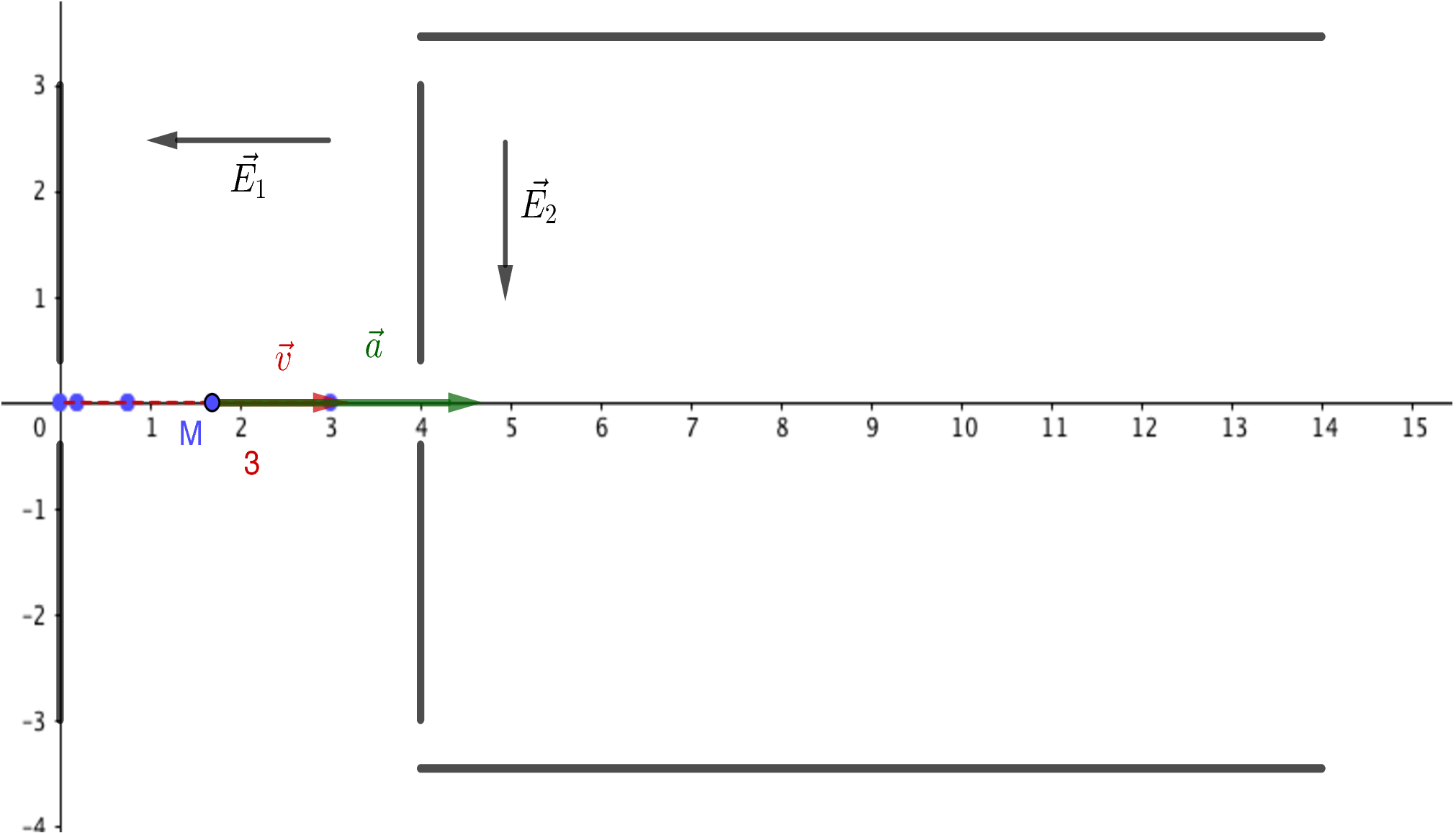
Deuxième phase : déviation de l’électron
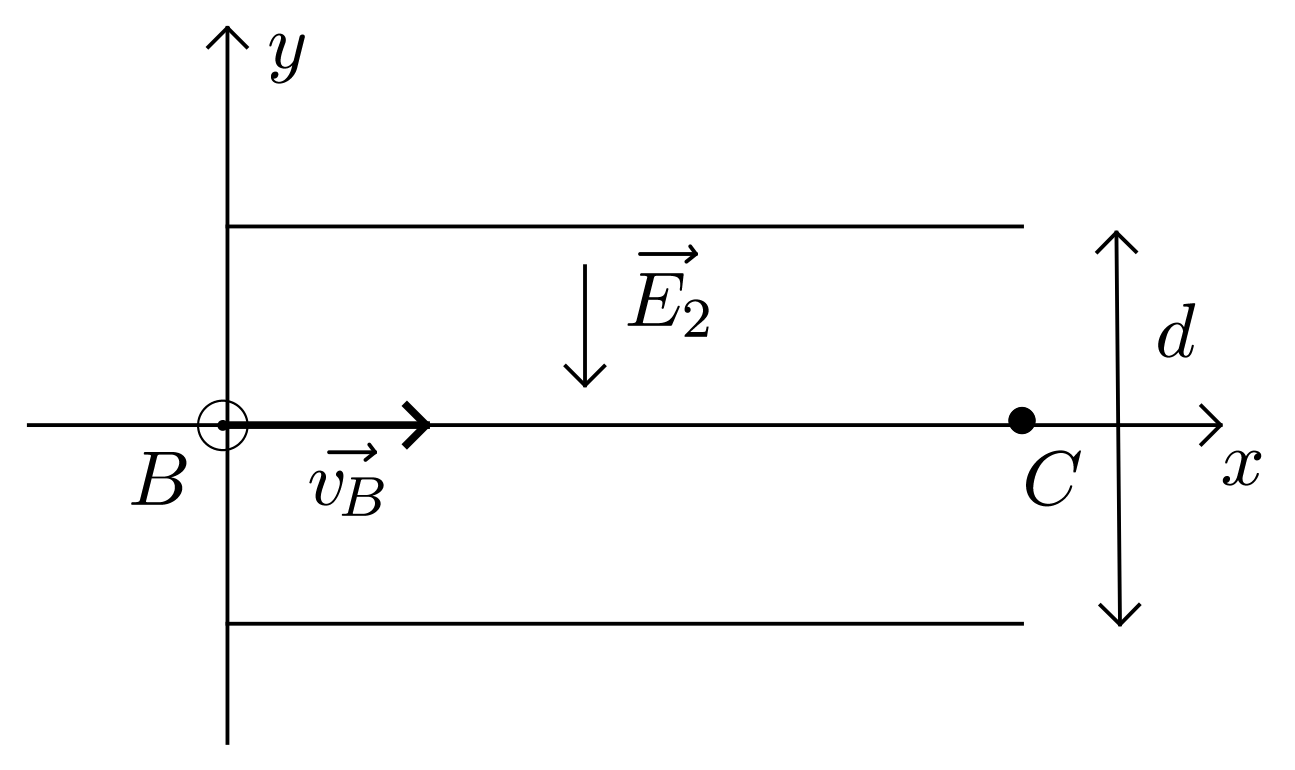
L’électron entre maintenant dans une nouvelle zone dans laquelle règne un champ électrique $\vec{E}_2$ avec la vitesse $\vec{v}_B$ déterminée dans la section précédente.
On redéfinit l’origine des dates, $t = 0$ à l’instant où l’électron entre dans cette zone, et le repère d’espace, désormais $(B ; \vec{i}, \vec{j}, \vec{k})$.
On cherche à vérifier si l’électron peut quitter cette zone sans toucher l’une des armatures.
Données
$BC = \pu{6,0 cm}$ ; $d = \pu{3,0 cm}$ ; $E_2 = \pu{1,0e4 V.m-1}$.
Détermination des équations horaires — Lois de Newton
Caractériser le mouvement.
Réponse
-
Système : {électron}
-
Interactions :
-
Système - champ de pesanteur : négligeable.
-
Système - champ électrique, modélisée par la force électrique : $\vec{F}_{2 el} = - e \vec{E}_2$
-
-
Référentiel : {terrestre supposé galiléen}
-
Schématisation : (pas à l’échelle)
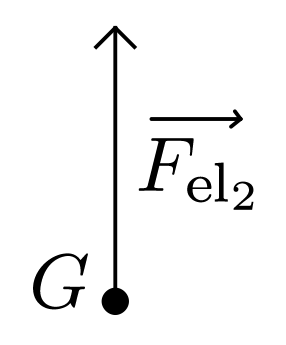
-
Deuxième loi de Newton : puisque la masse $m_e$ d’un électron est constante, on peut écrire $$ m_e\, \vec{a}_2 = \vec{F}_{2 el} = - e \vec{E}_2 $$ soit $$ \boxed{ \vec{a}_2 = - \dfrac{e}{m_e}\, \vec{E}_2 } $$ Le mouvement est uniformément accéléré.
Réponse
-
Projection de la deuxième loi de Newton sur le système d’axes $(x’ x)$, $(y’ y)$, $(z’ z)$ muni du repère $(B ; \vec{i}, \vec{j}, \vec{k})$ (non dessiné sur le schéma) :
-
Projections des conditions initiales et des grandeurs apparaissant dans la relation de Newton : $$ \overrightarrow{BM} (0) = \left(\begin{array}{c} 0\cr 0\cr 0 \end{array}\right) \text{ ; } \vec{v}_B = \vec{v}_2 (0) = \left(\begin{array}{c} v_B\cr 0\cr 0 \end{array}\right) \text{ ; } \vec{a}_2 = \left(\begin{array}{c} a_{2 x}\cr a_{2 y}\cr a_{2 z} \end{array}\right)$$
$$ \vec{E}_2 = \left(\begin{array}{c} 0\cr -E_2\cr 0 \end{array}\right) $$
- Composantes de l’accélération : $$ \begin{pmatrix} a_{2 x}\cr a_{2 y}\cr a_{2 z} \end{pmatrix} = - \dfrac{e}{m_e}\, \begin{pmatrix} 0\cr -E_2\cr 0 \end{pmatrix} = \begin{pmatrix} 0\cr \dfrac{eE_2}{m_e}\cr 0 \end{pmatrix} $$ donc $$ \boxed{ \begin{cases} a_{2 x} = 0\cr a_{2 y} = \dfrac{eE_2}{m_e}\cr a_{2 z} = 0 \end{cases} } $$ Le mouvement est donc uniformément accéléré selon l’axe $(A y)$. Il n’est pas possible de conclure quant à la forme du mouvement selon les axes $(A x)$ et $(A z)$ : mouvements uniformes ou pas de mouvement.
Réponse
Composantes de la vitesse : $$ \begin{cases} a_{2 x} &= \dfrac{\mathrm{d}v_{2 x}}{\mathrm{dt}} = 0\cr a_{2 x} &= \dfrac{\mathrm{d}v_{2 y}}{\mathrm{dt}} = \dfrac{eE_2}{m_e}\cr a_{2 z} &= \dfrac{\mathrm{d}v_{2 z}}{\mathrm{dt}} = 0 \end{cases} $$ donc $$ \begin{cases} v_{2 x} (t) = A\cr v_{2 y} (t) = \dfrac{eE_2}{m_e}\, t + B\cr v_{2 z} (t) = C \end{cases} $$
- Conditions initiales pour la vitesse : $$ \begin{cases} v_{2 x} (0) &= A = v_B\cr v_{2 y} (0) &= B = 0\cr v_{2 z} (0) &= C = 0 \end{cases} $$ Finalement $$ \boxed{ \begin{cases} v_{2 x} (t) &= v_B\cr v_{2 y} (t) &= \dfrac{eE_2}{m_e} t\cr v_{2 z} (t) &= 0 \end{cases} } $$ Il n’y a aucun mouvement selon l’axe $(B z)$ alors que le mouvement est uniforme selon l’axe $(B x)$.
Réponse
-
Composantes du vecteur position : $$ \begin{cases} v_{2 x} (t) &= \dfrac{\mathrm{d}x_2}{\mathrm{dt}} = v_B\cr v_{2 y} (t) &= \dfrac{\mathrm{d}y_2}{\mathrm{dt}} = \dfrac{eE_2}{m_e} t\cr v_{2 z} (t) &= \dfrac{\mathrm{d}z_2}{\mathrm{dt}} = 0 \end{cases} $$ donc $$ \begin{cases} x_2 (t) &= v_B t + D\cr y_2 (t) &= \dfrac{1}{2}\, \dfrac{eE_2}{m_e}\, t^2 + E\cr z_2 (t) &= F \end{cases} $$
-
Conditions initiales pour la position : $$ \begin{cases} x_2 (0) &= D = 0\cr y_{12} (0) &= E = 0\cr z_2 (0) &= F = 0 \end{cases} $$
-
Finalement $$ \boxed{ \begin{cases} x_2 (t) = v_B t\cr y_2 (t) = \frac{1}{2} \frac{eE_2}{m_e} t^2\cr z_2 (t) = 0 \end{cases} } $$
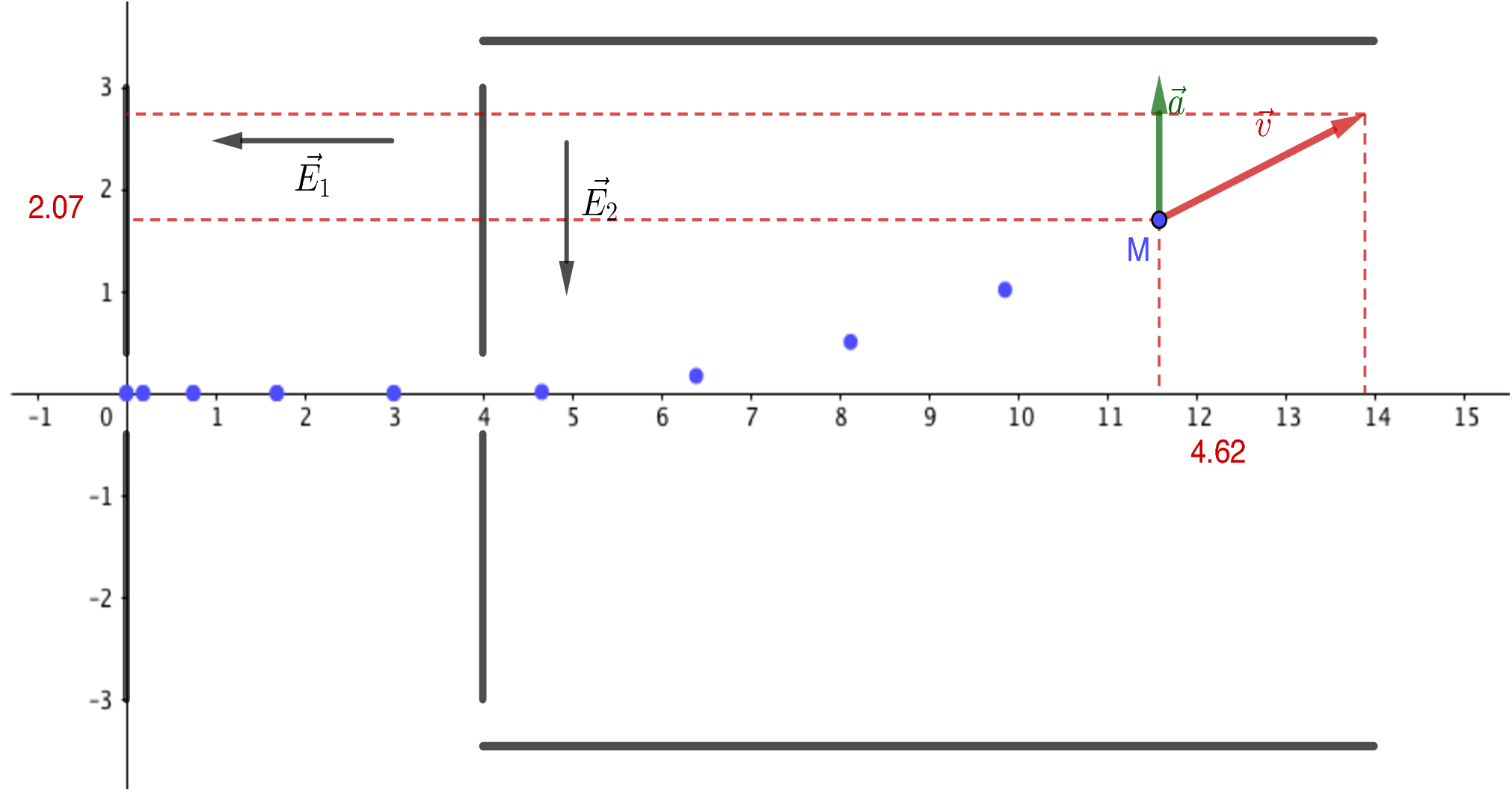
Équation de la trajectoire
Réponse
Pour obtenir l’équation de la trajectoire, il faut éliminer le temps des équations horaires : $$ t = \dfrac{x_2}{v_B} $$ donc $$ \boxed{ y_2 (x) = \dfrac{1}{2}\, \dfrac{eE_2}{m_e} \left( \dfrac{x_2}{v_B} \right)^2 } $$ C’est une parabole orientée vers le haut.
À quelle condition l’électron peut-il quitter cette zone de l’espace sans toucher l’armature supérieure ?
Réponse
On fait l’hypothèse que l’électron va toucher l’armature supérieure. Soit $x_{2 p}$ l’abscisse de l’électron lorsque cet évènement intervient.
À partir de l’équation de la trajectoire (c’est aussi possible à partir des équations horaires), on peut déterminer que : $$ y_2 (x_{2 p}) = \dfrac{d}{2} = \dfrac{1}{2}\, \dfrac{eE_2}{m_e} \left( \dfrac{x_{2 p}}{v_B} \right)^2 $$ soit $$ x_{2 p} = v_B \sqrt{\frac{m_e d}{eE_2}} $$ L’électron ne touche pas l’armature supérieure si $x_{2 p} > BC$, donc si $$ x_{2 p} = v_B \sqrt{\frac{m_e d}{eE_2}} > BC $$
A.N. $x_{2 p} = \pu{10,3 cm} > \pu{6,0 cm}$
Réponse
La question précédente a fourni l’expression suivante : $$ v_B \sqrt{\frac{m_e d}{eE_2}} > BC \iff v_B \sqrt{\frac{m_e d^2}{eU_2}} > BC $$ puisque $E_2 = \dfrac{U_2}{d}$. Finalement $$ \boxed{ \dfrac{m_e d^2 v_B^2}{e\, BC^2} > U_2 } $$
Coordonnées du points de sortie
Réponse
L’électron quitte la deuxième zone lorsque $$ \boxed{ x_{2 C} = BC } $$ donc lorsque $$ \boxed{ y_2 (x_{2 C}) = \dfrac{1}{2}\, \dfrac{eE_2}{m_e} \left( \dfrac{BC}{v_B} \right)^2 } $$
Dernière phase
Réponse
Au-delà des deux première zones, il n’existe plus de champ électrique et l’on peut toujours négliger le poids de l’électron. Ce dernier n’est donc soumis à aucune force, son mouvement est rectiligne et uniforme depuis le point de sortie de la deuxième zone.