Applications de la radioactivité à la datation
Doses de radiations
Décroissance radioactive
Loi de décroissance
Évolution du nombre de noyaux d’un échantillon de noyaux radioactifs
Soit un échantillon contenant des atomes radioactifs susceptibles de se désintégrer selon l’un des modes définis dans le cours.
- Écrire l’équation de désintégration du césium 137, émetteur $\beta^-$.
Réponse
$$ \ce{_{55}^{137}Cs –> _{56}^{137}Ba + _{-1}^{0}e + \bar{\nu}_e} $$
Une désintégration radioactive est par nature probabiliste : c’est un phénomène aléatoire. À chaque instant, il y existe une certaine probabilité pour qu’un noyau se désintègre entre deux dates $t$ et $t + \Delta t$. On note cette probabilité $\lambda, \Delta t$ où $\lambda$ est une constante caractéristique du noyau considéré et indépendante du temps.
[Lire]Radioactivité et physique nucléaire, introduction
Radioactivité et physique nucléaire
Premier principe de la thermodynamique : exercices
Température de contact
Différents corps placés longtemps au contact Ies uns des autres, finissent par atteindre un état d’équilibre thermique caractérisé par une même température $T_e$.
Pourtant, lorsque l’on touche un objet en marbre ou un objet en bois placés tous deux depuis longtemps dans une même pièce, la sensation est différente : sensation de froid dans le cas du marbre qui n’existe pas pour le contact avec le bois.
Propriétés des solutions d'ammoniac
Une solution commerciale $S_0$ d’ammoniac $\ce{NH3 (aq)}$ de concentration $C_0 = \pu{1,1 mol.L-1}$ peut être utilisée, après dilution, comme produit nettoyant (éviers, lavabos, …) ou comme produit détachant (moquette, tapis, …).
On se propose d’étudier la solution $S$ d’ammoniac de concentration $C_S$ : $S$ étant 100 fois plus diluée que $S_0$.
Données :
-
Produit ionique de l’eau : $K_e = \pu{1,0e–14}$.
-
$\text{pK}_a$ de quelques couples acide/base :
- $\ce{H3O+/H2O}$ : $\text{pK}_{a1} = \pu{0,0}$ ;
- $\ce{NH4^+/NH3}$ : $\text{pK}_{a2} = \pu{9,2}$ ;
- $\ce{H2O/HO–}$ : $\text{pK}_{a3} = \pu{14,0}$.
-
Valeurs des conductivités molaires ioniques (en $\pu{S.m2.mol-1}$) :
[Lire]
Annale : Le bleu de bromophénol
Le bleu de bromophénol est un indicateur coloré dont la forme acide, notée $\ce{HIn}$, est jaune et dont la forme basique, notée $\ce{In^−}$, est bleue.
- Préparation de la solution mère :
- On prépare, dans une fiole jaugée, deux litres d’une solution mère $S_0$ de bleu de bromophénol de concentration molaire en soluté apporté $C_0 = \pu{3,0e-5 mol.L-1}$.
Première partie : Étude de la solution mère
On considère un volume $V = \pu{100 mL}$ de solution $S_0$ dont le pH est de 4,7.
[Lire]Premier principe de la thermodynamique
À maîtriser avant le début de ce cours : Travail, Force conservative, Force non conservative, Énergie potentielle d’interaction, Énergie cinétique, Énergie mécanique.
À la recherche d’une grandeur énergétique conservative
Une grandeur caractérisant l’état d’un système est dite conservative si elle reste constante lorsque le système est isolé.
Les grandeurs conservatives sont très importantes en physique, leur utilisation permet souvent de comprendre simplement l’évolution des systèmes.
Une masse $m$ est mise en mouvement au contact de la Terre. L’expérience
montre que, à cause des frottements solides, la masse finit
immanquablement par s’arrêter après avoir parcouru une distance $d$.
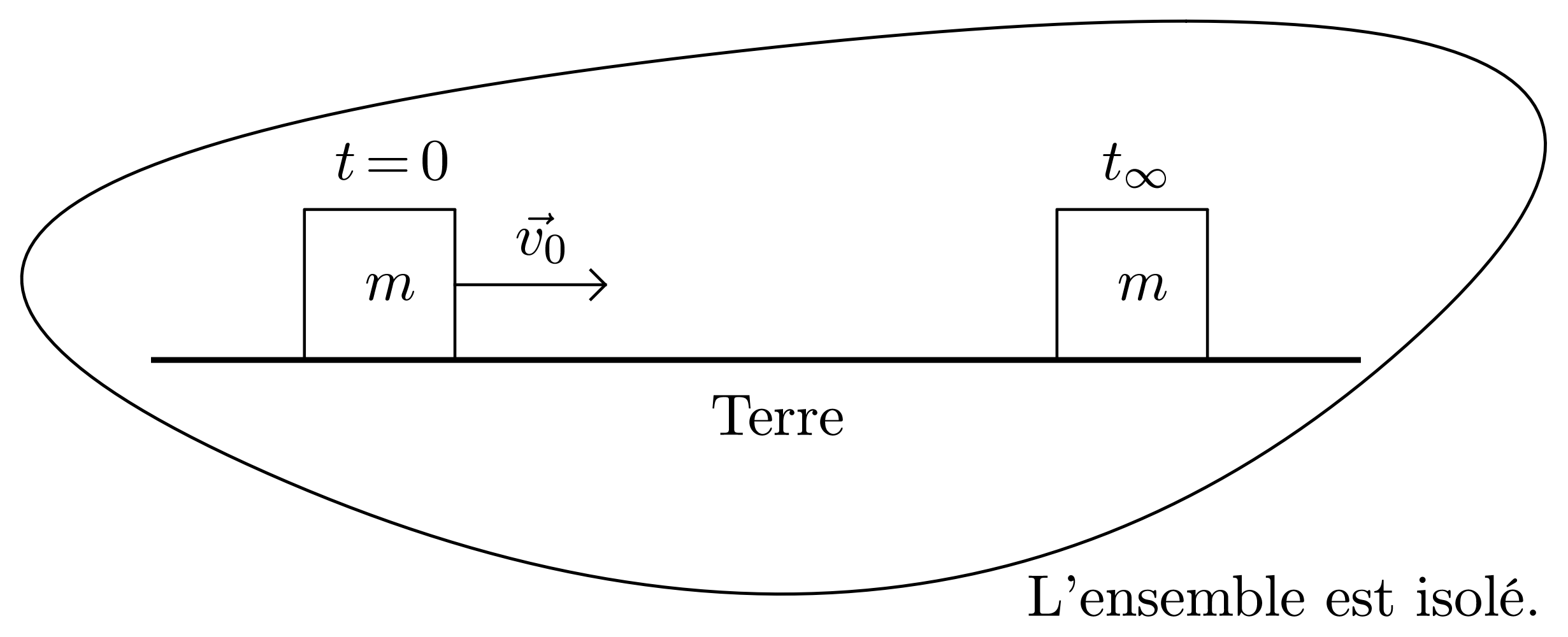
- Démontrer que l’énergie mécanique n’est pas une grandeur conservative.
Réponse
Dans le référentiel du laboratoire, $E_M (t = 0) = \dfrac{1}{2} m\, v_0^2 + E_{PP}$ et $E_M (t_{\infty}) = E_{PP}$. Donc $\Delta E_M = E_M (t_{\infty}) - E_M(t = 0) = - \dfrac{1}{2}\, m\, v_0^2 < 0$.
[Lire]