Terminale Spé PC

Documents

Solution physiologique

Courant électrique

• Dans un circuit solide, aucune charge positive ne peut se déplacer. Les électrons circulent donc dans le sens opposé au sens de circulation du courant électrique.
• Toute solution ionique est électriquement neutre : elle contient donc forcément des cations et des anions. Les cations circulent dans le même sens que le courant électrique alors que les anions circulent dans le sens opposé au sens de circulation du courant électrique.

Conductance d’une solution ionique

Résistance et conductance

Rappel

Lorsqu’on mesure la tension électrique $U$ aux bornes d’un conducteur ohmique et l’intensité $I$ du courant électrique le traversant, on constante que ces deux grandeurs sont proportionnelles : $U = R\cdot I$. $R$ le coefficient de proportionnalité est appelé la résistance électrique du conducteur ohmique. On peut aussi écrire cette relation sous la forme $I = G \cdot U$ où $G = 1/R$ est la conductance du conducteur ohmique (unité : $\pu{S}$, siemens).

Il est assez facile de calculer la concentration massique ou la concentration molaire lorsqu’on sait comment la solution a été préparée : il suffit de diviser la masse (ou la quantité de matière) de soluté apporté par le volume du solvant¹.

Mais comment déterminer la concentration en soluté apporté d’une solution que l’on n’a pas préparé ? Comment vérifier la valeur de la concentration en soluté apporté d’une solution ?

Ce chapitre introduit une méthode permettant de répondre à ces questions à la condition que la solution soit colorée !

[Lire]

Livre scolaire

• 32, 34, 33 pages 509 et 510

Annale

• Autour du papillon

Ne pas traiter les première et deuxième partie (seulement la partie 3).

• D'où viennent les couleurs des ailes des papillons ?

Interférences

Par la suite, toutes les ondes étudiées seront sinusoïdales, de même fréquence $f$.

Un exemple de montage d’étude d’une figure d’interférence

Schéma de principe

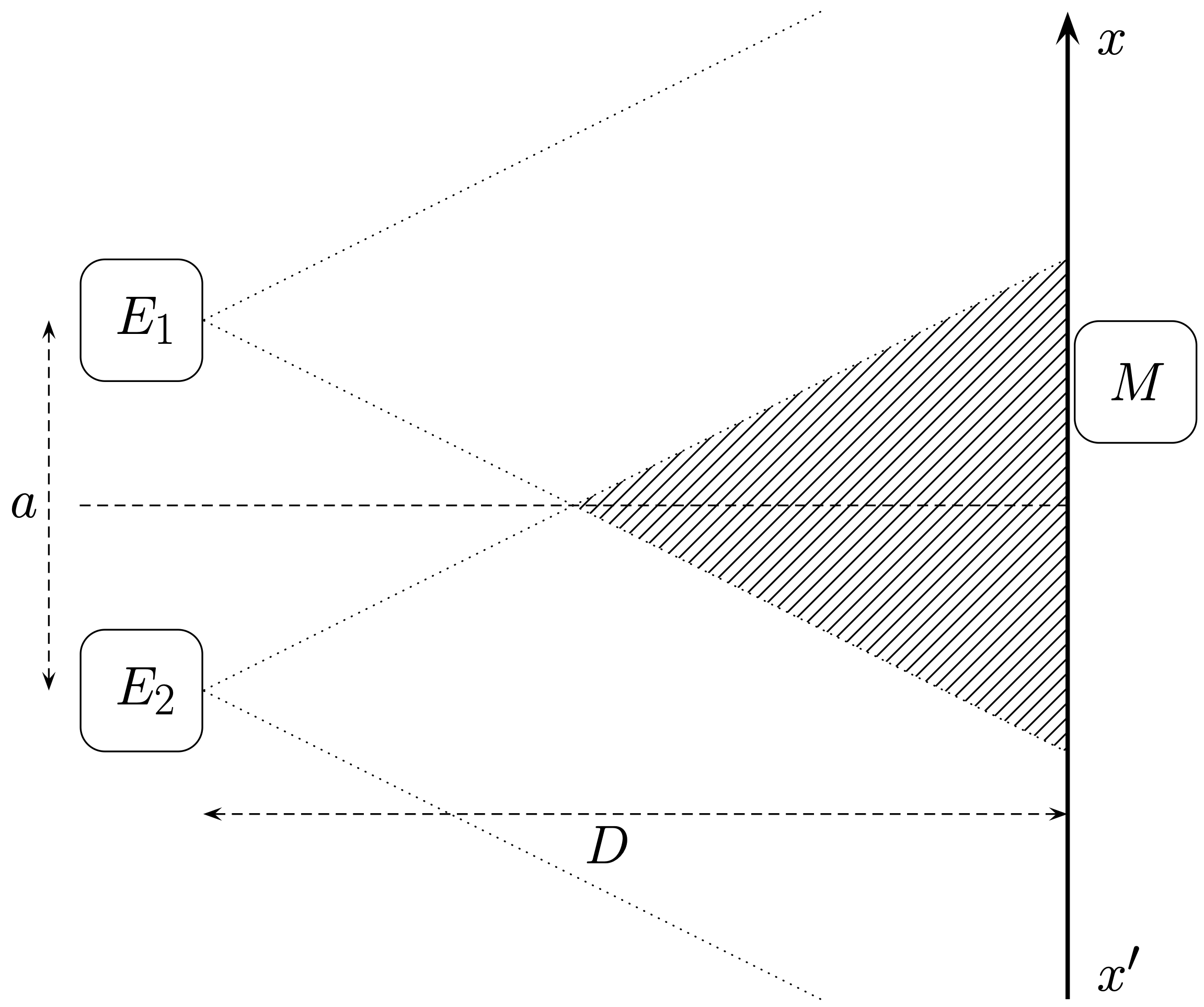
Deux ondes sinusoïdales de même fréquence $f$ sont émises par les deux émetteurs $E_1$ et $E_2$. L’émission de ces ondes s’effectuant dans un cône, ces ondes ne se superposent que dans la zone hachurée sur le schéma : c’est le champ d’interférence. Dans toute cette région, ces ondes interférent.

Émission de bips sonores par deux émétteurs

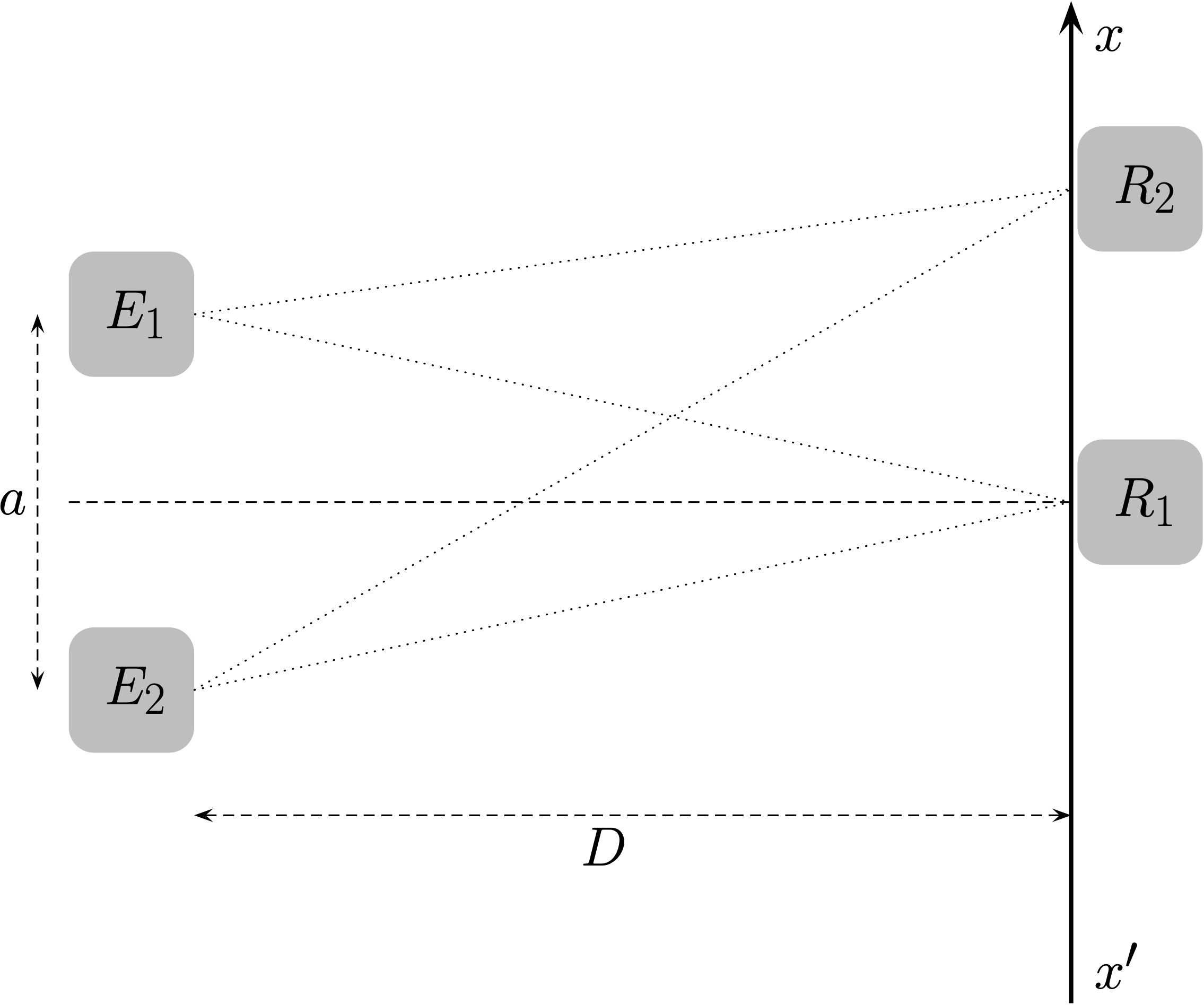
1. Deux émetteurs synchronisés, $E_1$ et $E_2$, émettent chacun un bip sonore, à la date $t=\pu{0 s}$ alors qu’un récepteur $R$ se trouve à la position $R_1$.
   Combien de bips perçoit le récepteur ? Pourquoi ?

Réponse

Le récepteur perçoit un seul bip puisque les deux signaux doivent parcourir la même distance à la même vitesse (car ils se propagent dans le même milieu) et arrivent donc à la même date.

2. On place cette fois le récepteur à la position $R_2$. Que perçoit le récepteur dans ce cas ? Pourquoi ?

Réponse

Le signal issu de l'émetteur $E_1$ doit parcourir une plus petite distance que le signal issu de l'émetteur $E_2$ (ces signaux se propagent avec la même célérité puisqu'ils sont dans le même milieu). Le récepteur perçoit donc deux signaux : celui issu de $E_1$ puis celui issu de $E_2$.

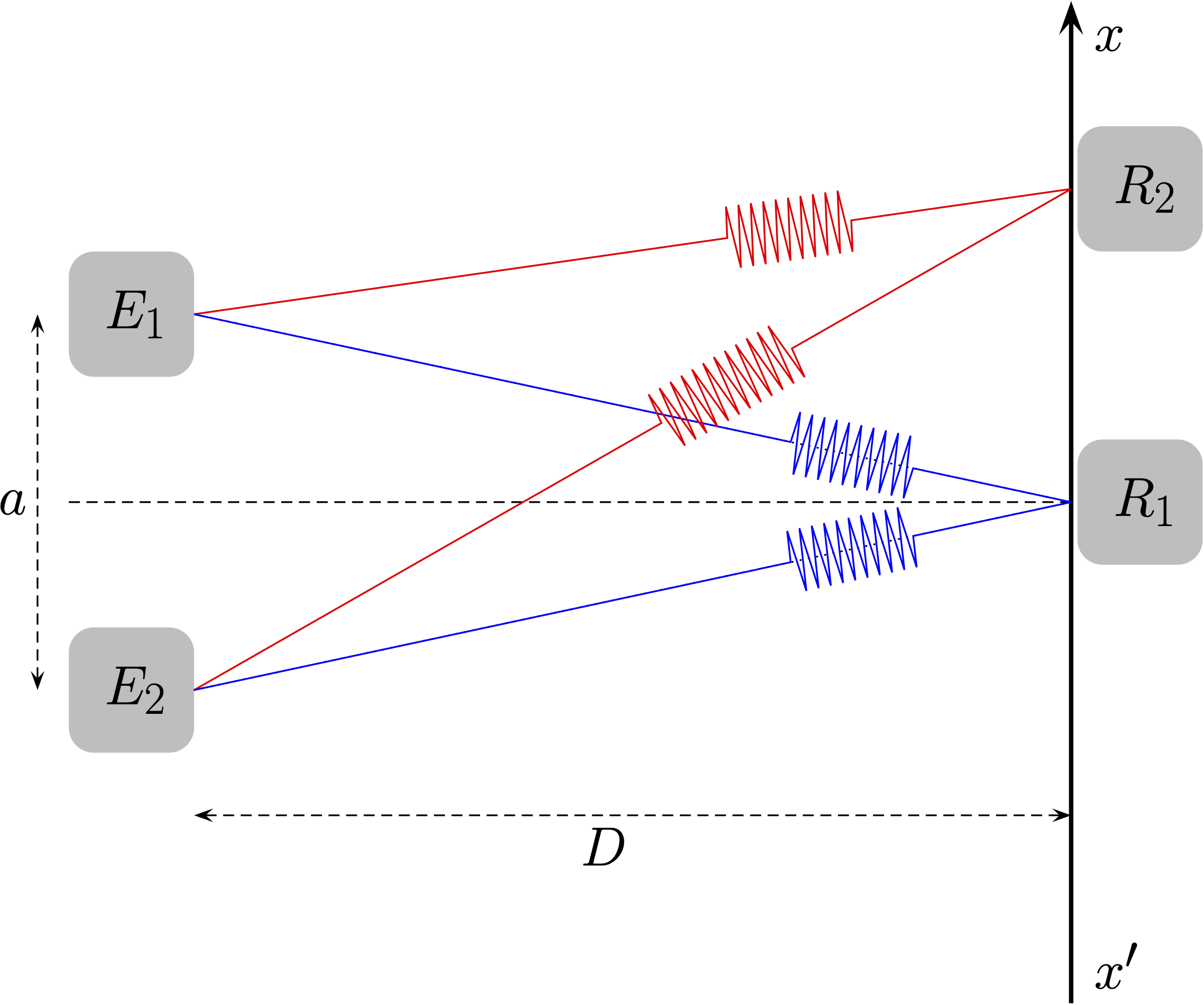
3. Si on note $t_1$ la date à laquelle le récepteur positionné en $R_2$ reçoit le signal issu de $E_1$ et $t_2$ la date à laquelle ce même récepteur reçoit le signal issu de $E_2$, établir l’expression du retard $\tau$ avec lequel le deuxième signal arrive par rapport au premier.

Deux élèves, lors d’une séance de travaux pratiques, réalisent l’expérience suivante. Ils branchent un générateur basse fréquence délivrant une tension sinusoïdale aux bornes d’un haut-parleur. À l’aide de deux microphones identiques reliés à une carte d’acquisition, ils visualisent les signaux électriques $u_1 (t)$ et $u_2 (t)$ produits lors de la réception du son (figures 1 et 2). Les deux microphones $M_1$ et $M_2$ sont séparés par une distance $d$.

Schématisation du montage Figure 1 Figure 2

[Lire]

Documents

Affaiblissement des signaux

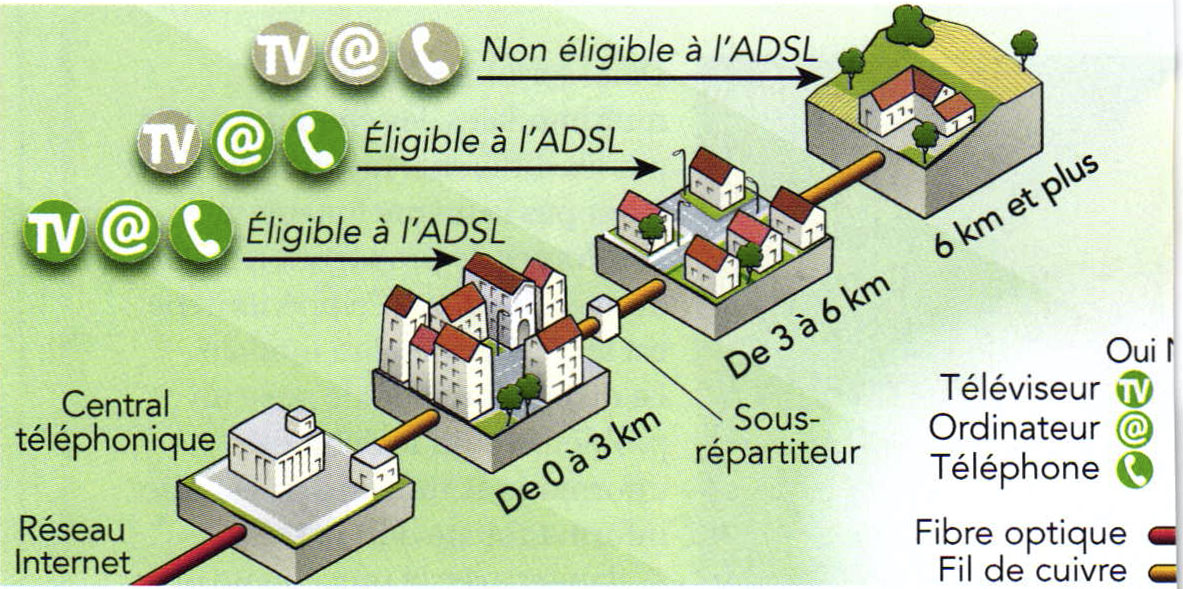
« Un courant électrique passant au travers d’un conducteur dissipe une partie de son énergie sous forme de chaleur (pertes par effet Joule). Il en résulte une diminution de la puissance de ce signal. Les pertes augmentent avec la résistance du câble. La résistance est elle-même fonction de la longueur du câble, de son diamètre et de sa résistivité¹ […] Les technologies xDSL² font passer des signaux électriques à haute fréquence dans les câbles téléphoniques, constitués de fils de cuivre. Compte tenu de ces hautes fréquences, un effet de peau³ apparaît ; il a pour conséquence d’augmenter fortement la résistance du câble, et donc d’atténuer d’autant plus le signal utile en raison du phénomène décrit précédemment. […] Il découle de ce phénomène que certaines habitations, proches des centraux téléphoniques […] bénéficient de débits élevés (jusqu’à $\pu{20 Mbit/s}$, permettant un grand confort d’usage et des services innovants tels que la télévision par ADSL), tandis que d’autres plus éloignés doivent se contenter de $\pu{512 kbit/s}$ — et ce pour un prix d’abonnement identique. »

Exercice

La puissance lumineuse d’un signal transmis par une fibre optique décroît avec la distance qu’il parcourt.

Le coefficient d’atténuation linéique $\alpha$ caractérise cette décroissance. ll est défini par la relation : $$\alpha = \dfrac{10}{L} \, \log \left( \dfrac{ \cal I_e }{ \cal I_s } \right)$$ $\alpha$ est exprimé en décibel par unité de longueur ($\pu{dB/m}$), $L$ est la longueur de la fibre en mètre, $\cal I_e$ et $\cal I_s$ sont respectivement les intensités en entrée et en sortie du signal.

Le texte ci-dessous retrace succinctement l’évolution de quelques idées à propos de la nature de la lumière. Extraits d’articles parus dans l’ouvrage « Physique et Physiciens » et dans des revues « Sciences et vie ».

Huyghens (1629-1695) donne à la lumière un caractère ondulatoire par analogie à la propagation des ondes à la surface de l’eau et à la propagation du son.
Pour Huyghens, le caractère ondulatoire de la lumière est fondé sur les faits suivants :