Exercice
La puissance lumineuse d’un signal transmis par une fibre optique décroît avec la distance qu’il parcourt.
Le coefficient d’atténuation linéique $\alpha$ caractérise cette décroissance. ll est défini par la relation : $$ \alpha = \dfrac{10}{L} \, \log \left( \dfrac{ \cal I_e }{ \cal I_s } \right) $$ $\alpha$ est exprimé en décibel par unité de longueur ($\pu{dB/m}$), $L$ est la longueur de la fibre en mètre, $\cal I_e$ et $\cal I_s$ sont respectivement les intensités en entrée et en sortie du signal.
Ce coefficient d’atténuation $\alpha$ dépend du matériau et de la longueur d’onde $\lambda$ de la radiation utilisée.
Le graphique ci-dessous représente le coefficient d’atténuation linéique dans une fibre optique en fonction de la longueur d’onde de la radiation utilisée.
-
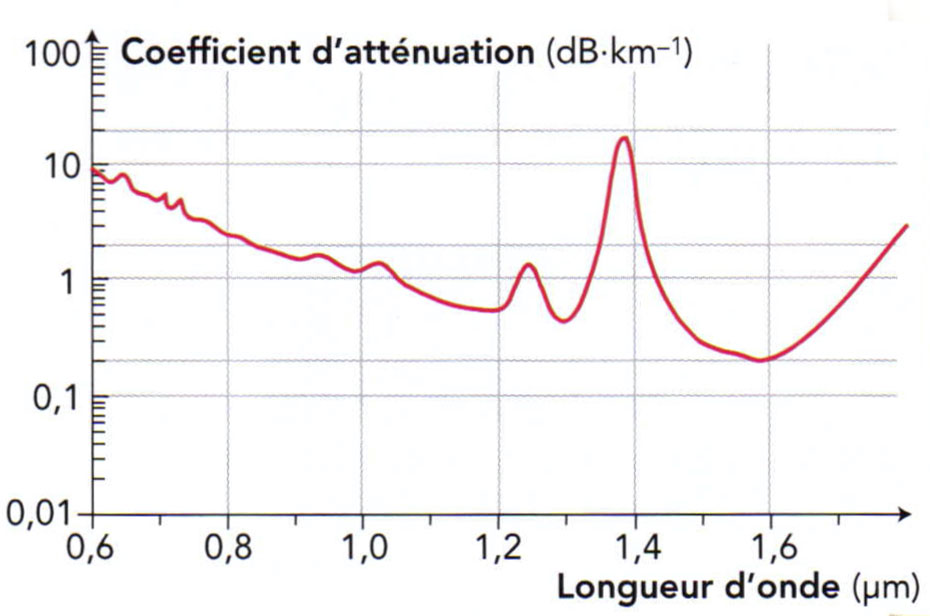
Dans le domaine du spectre électromagnétique concerné, quelle radiation est transmise avec le moins d’atténuation ?
-
Calculer alors pour cette radiation le rapport des puissances d’entrée et de sortie $\left( \dfrac{ \cal I_e }{ \cal I_s } \right)$ pour une fibre de $\pu{100 km}$ de longueur.
-
Lequel des phénomènes suivants peut être à l’origine du pic observé pour $\lambda \approx \pu{1,4 \mu m}$ : la diffraction ; la transmission ; l’absorption ; la réfraction ; la réflexion.
La maîtrise des procédés de fabrication des fibres optiques permet de limiter considérablement leur coefficient d’atténuation linéique.
Par exemple, il reste 1,00 % de l’intensité en entrée après une propagation sur une distance de $\pu{100 km}$ de signaux de longueur d’onde dans le vide égale à $\pu{1 550 nm}$. Cette puissance est suffisante pour que ces signaux soient détectés.
- Quel est le coefficient d’atténuation linéique ?
En résumé
Au cours de sa propagation une onde s’atténue. Cette atténuation existe :
- parce que l’énergie se répartie sur des fronts d’onde de plus en plus grand au fur et à mesure que l’onde s’éloigne de sa source ;
- parce, dans certains cas, l’onde cède une partie (ou la totalité) de son énergie au milieu dans lequel elle se propage.