Exercices du chapitre : corrections

Livre numérique Hatier

 Publié le October 23, 2022  |  9 minutes  |  1789 mots  |  David Latreyte

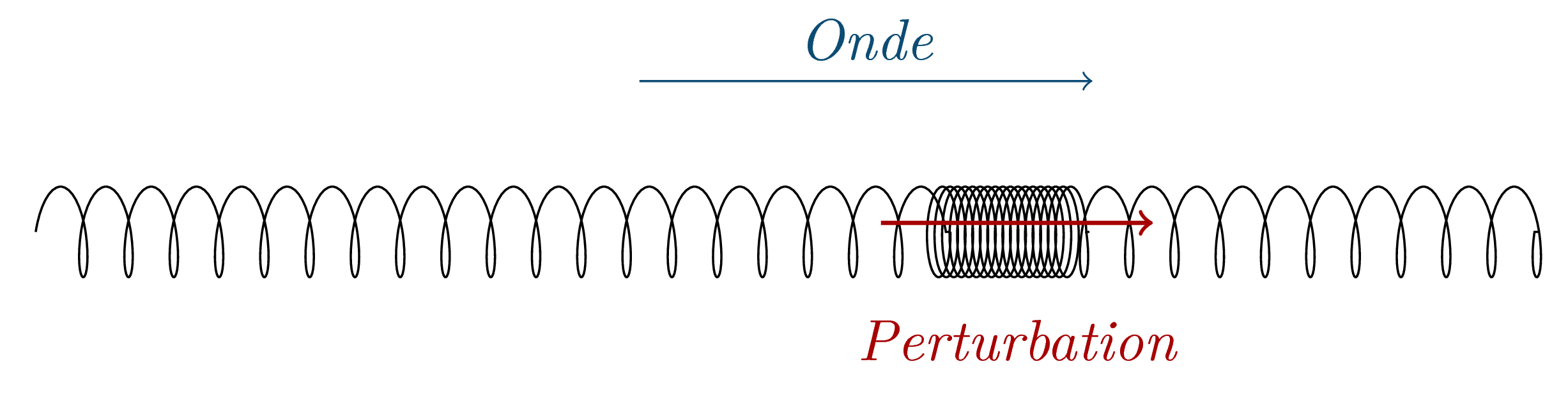
Exercice N°31, page 343 Corrigé La fréquence $f$ est le nombre de périodes par seconde, donc $$ f = \dfrac{1}{T} = \dfrac{1}{\pu{9,5 s}} = \pu{0,11 Hz} $$ La longueur d’onde est la distance parcourue par l’onde pendant une période (temporelle) $T$, donc $$ \lambda = vT = \pu{6,0 m.s^{- 1}} \times \pu{9,5 s} = \pu{57 m} $$ La longueur d’onde est la période spatiale de l’onde, c’est donc la plus petite longueur au bout de laquelle on retrouve le même état vibratoire dans le milieu. [Lire]
Ondes  Période  Fréquence  Longueur d'onde  Onde progressive  Onde mécanique  Onde sinusoïdale  Célérité 

Exercices de synthèse

 Publié le November 5, 2020  |  5 minutes  |  930 mots  |  David Latreyte

Calculer des durées de propagation Dans cette bande dessinée, Averell Dalton place son oreille sur un rail en acier afin d’entendre le train. Célérité du son : dans l’air : $\pu{340 m.s-1}$ ; dans l’acier : $\pu{5000 m.s-1}$. Le train, situé à une distance $d = \pu{1000 m}$ d’Averell, émet un bruit caractéristique en passant sur un aiguillage. Au bout de quelle durée $\Delta t_A$ ce bruit est-il perçu par Averell ? [Lire]
Ondes  Onde progressive  Onde mécanique  Célérité 

Caractéristiques des ondes mécaniques progressives

 Publié le October 28, 2020  |  7 minutes  |  1399 mots  |  David Latreyte

Qu’est ce qu’une onde progressive ? Étude de quelques simulations de propagation d’ondes mécaniques Onde progressive de compression Onde progressive se propageant le long d'une corde PhET Colorado Onde mécanique progressive Une perturbation/déformation correspond à la modification d’une propriété mécanique (vitesse, position, …) des constituants d’un milieu matériel. On appelle onde mécanique progressive le phénomène de propagation d’une perturbation dans un milieu matériel, de proche en proche, sans transport de matière mais avec transport d’énergie. [Lire]
Ondes  Période  Fréquence  Longueur d'onde  Onde progressive  Onde mécanique  Onde sinusoïdale  Célérité 

Exercices et Annale

 Publié le September 28, 2020  |  4 minutes  |  800 mots  |  David Latreyte

Livre scolaire 32, 34, 33 pages 509 et 510 Solutions Fichier au format pdf Annale Autour du papillon Ne pas traiter les première et deuxième partie (seulement la partie 3). D'où viennent les couleurs des ailes des papillons ? Correction de l'annale 1.1.1. Les chauve-souris émettent des ondes dont la fréquence est $f_e = \pu{50 kHz}$. L’homme peut entendre les sons dont les fréquences sont comprises entre $\pu{20 Hz}$ et $\pu{20 kHz}$. [Lire]
Différence de marche  Superposition  Période temporelle  Longueur d'onde  Retard  Déphasage  Ondes  Interférences  Doppler 

Conditions d’interférence de deux ondes sinusoïdales

 Publié le September 21, 2020  |  6 minutes  |  1107 mots  |  David Latreyte

Interférences On appelle interférence le résultat de la superposition de plusieurs ondes (mécaniques ou électromagnétiques) en un même point de l’espace. En physique, on distingue normalement deux phénomènes particuliers qui se produisent lorsqu’on additionne des ondes sinusoïdales : L’interférence, quand les ondes ont la même fréquence. Le battement, quand les fréquences des ondes sont légèrement différentes. Par la suite, toutes les ondes étudiées seront sinusoïdales, de même fréquence $f$. Un exemple de montage d’étude d’une figure d’interférence Schéma de principe Deux ondes sinusoïdales de même fréquence $f$ sont émises par les deux émetteurs $E_1$ et $E_2$. [Lire]
Différence de marche  Superposition  Période temporelle  Longueur d'onde  Retard  Déphasage  Ondes  Interférences 

Différence de marche et conséquence sur la superposition de deux ondes synchrones

 Publié le September 21, 2020  |  6 minutes  |  1130 mots  |  David Latreyte

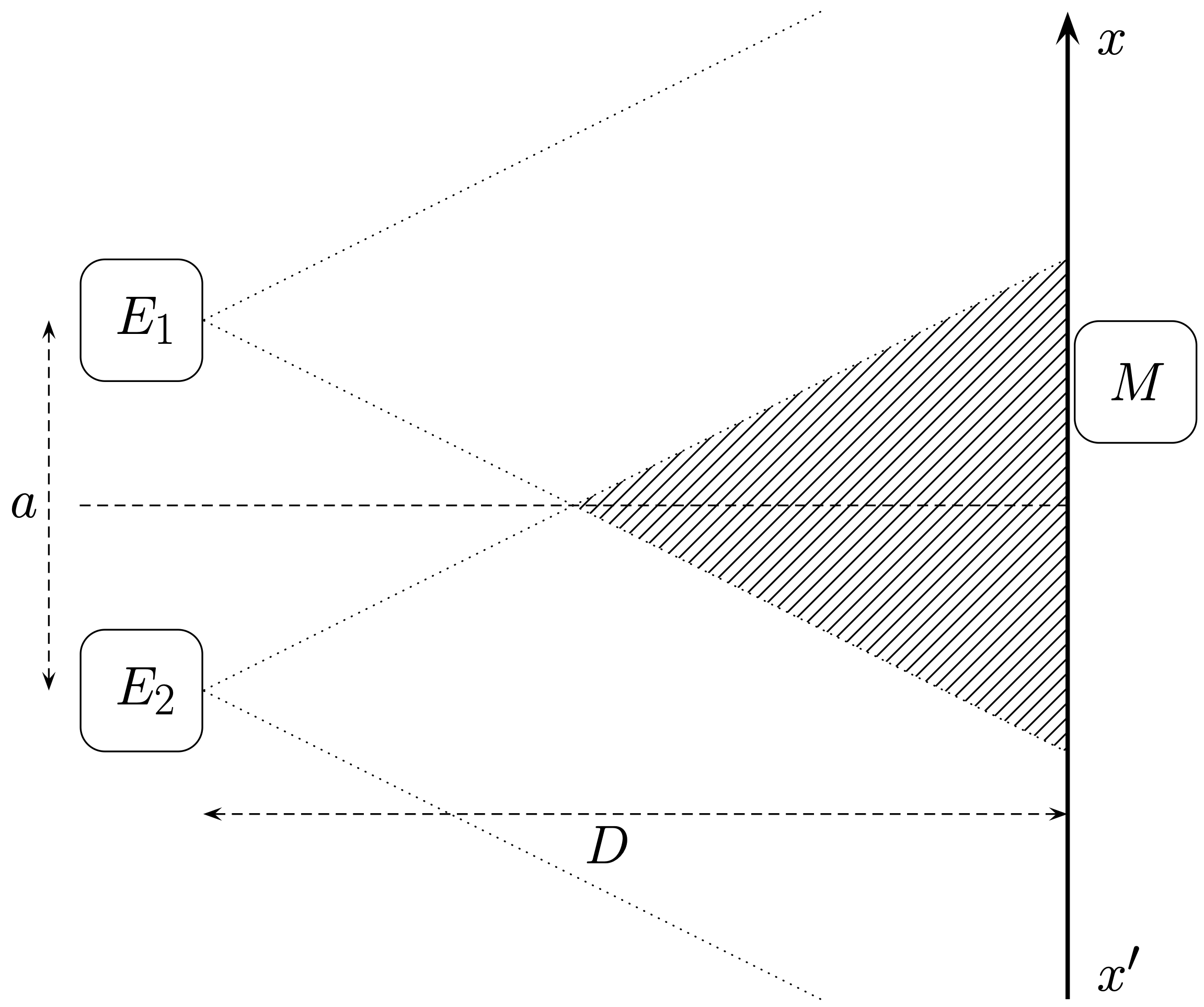
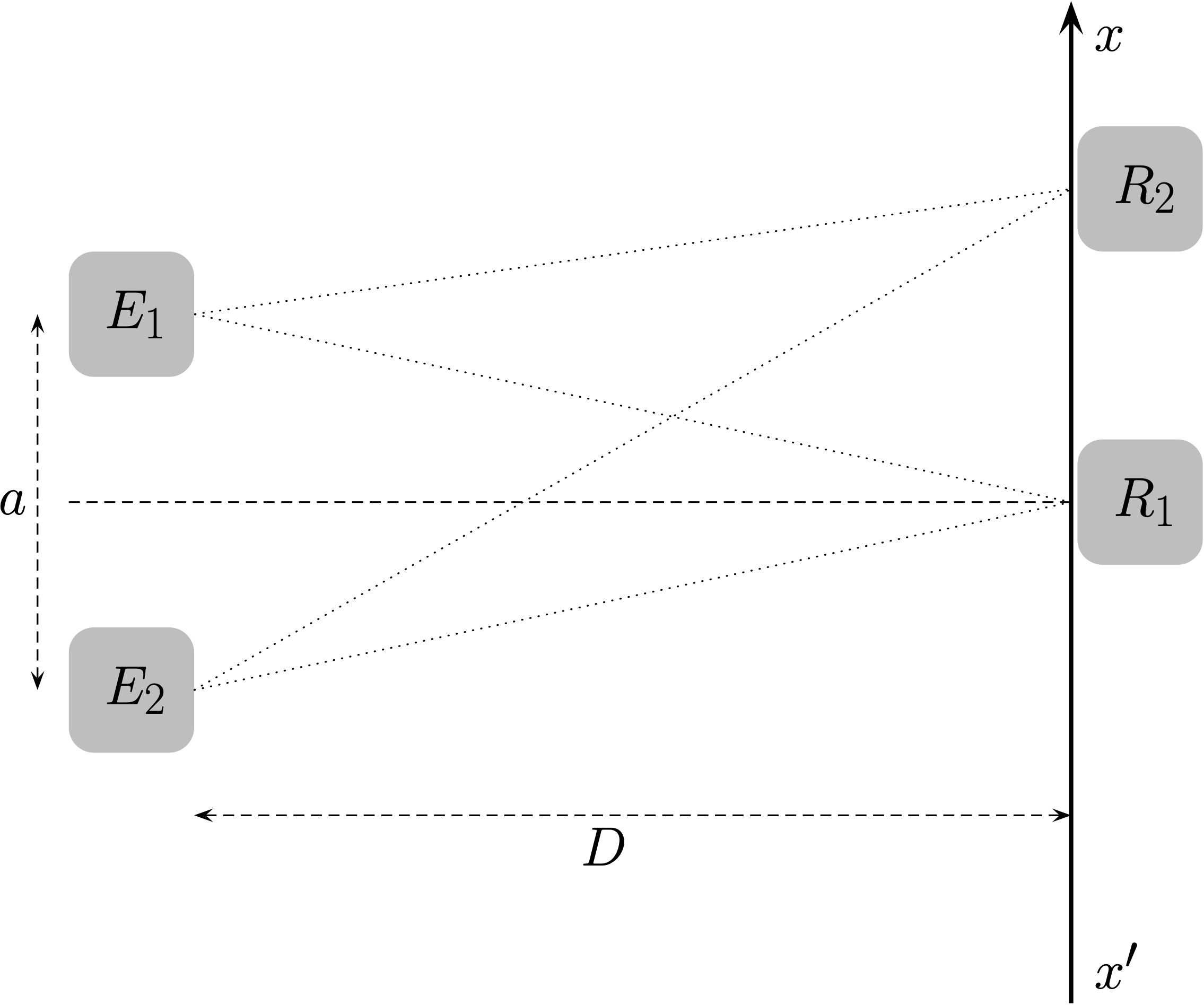
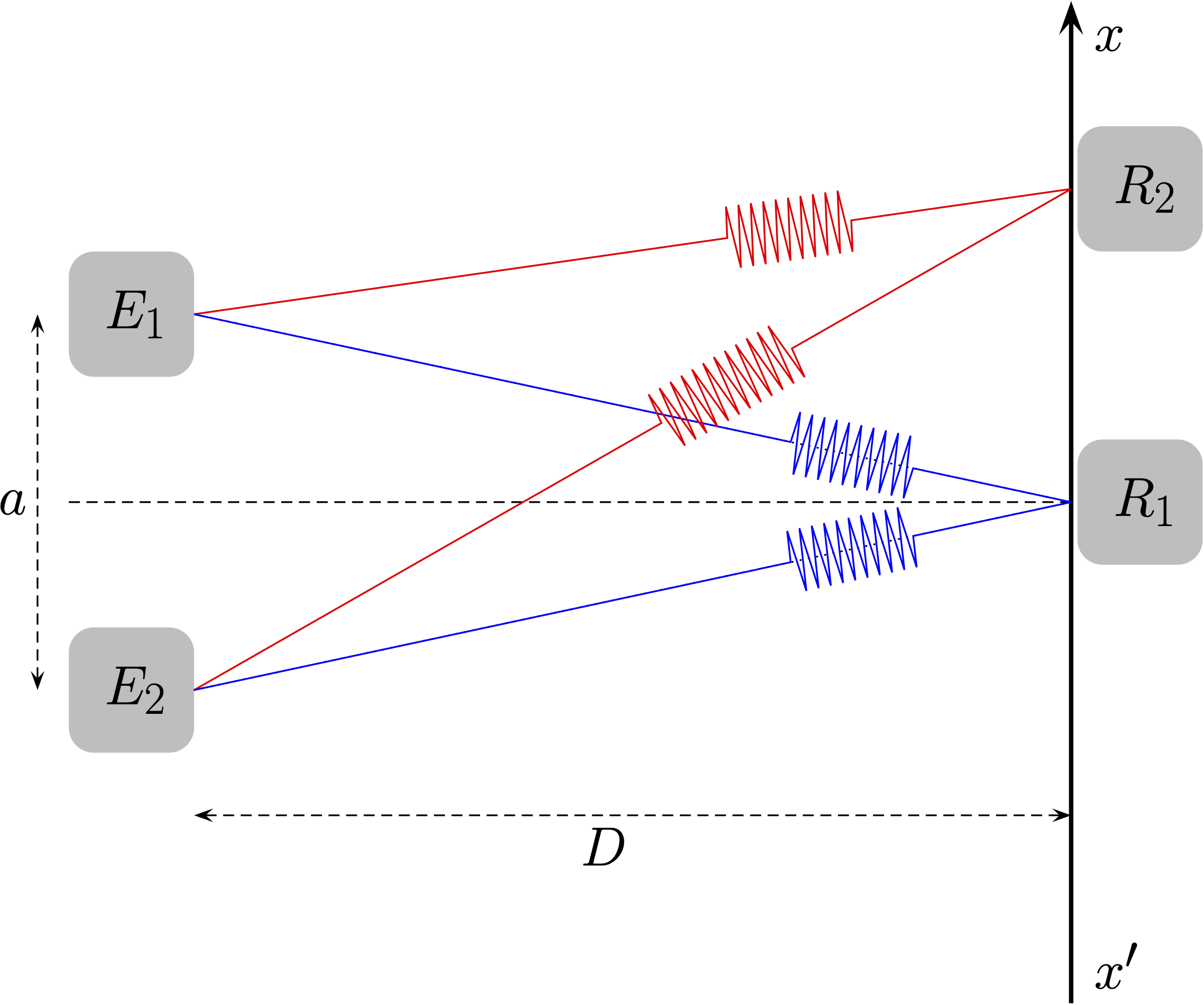Émission de bips sonores par deux émétteurs Deux émetteurs synchronisés, $E_1$ et $E_2$, émettent chacun un bip sonore, à la date $t=\pu{0 s}$ alors qu’un récepteur $R$ se trouve à la position $R_1$. Combien de bips perçoit le récepteur ? Pourquoi ? Réponse Le récepteur perçoit un seul bip puisque les deux signaux doivent parcourir la même distance à la même vitesse (car ils se propagent dans le même milieu) et arrivent donc à la même date. [Lire]
Différence de marche  Superposition  Période temporelle  Longueur d'onde  Retard  Déphasage  Ondes 

Retard, déphasage d'une onde sonore sinusoïdale

 Publié le September 19, 2020  |  5 minutes  |  1018 mots  |  David Latreyte

Deux élèves, lors d’une séance de travaux pratiques, réalisent l’expérience suivante. Ils branchent un générateur basse fréquence délivrant une tension sinusoïdale aux bornes d’un haut-parleur. À l’aide de deux microphones identiques reliés à une carte d’acquisition, ils visualisent les signaux électriques $u_1 (t)$ et $u_2 (t)$ produits lors de la réception du son (figures 1 et 2). Les deux microphones $M_1$ et $M_2$ sont séparés par une distance $d$. 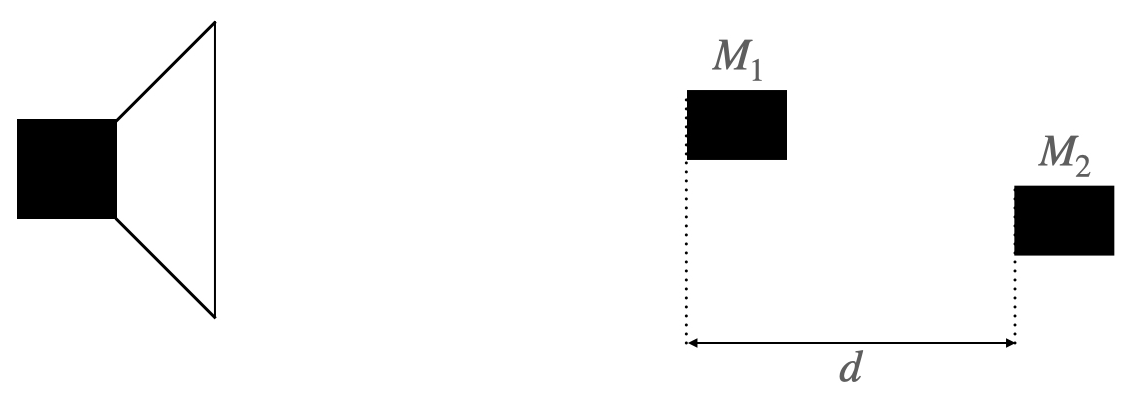Schématisation du montage Figure 1 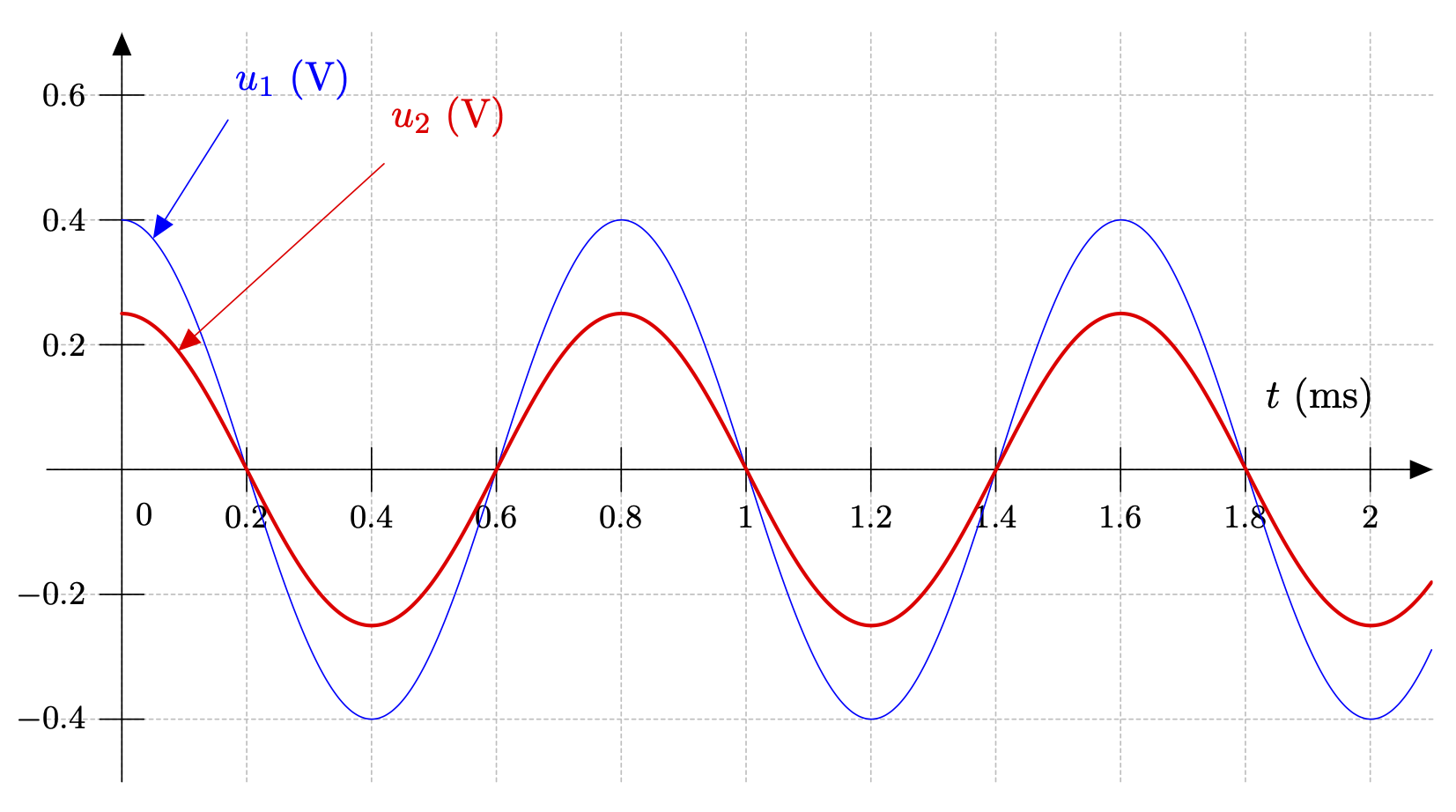Figure 2 Donnée La vitesse du son dans les conditions de l’expérience est de $\pu{340 m/s}$. [Lire]
Période temporelle  Longueur d'onde  Retard  Déphasage  Ondes 

Utiliser le réseau téléphonique pour surfer sur Internet

 Publié le September 18, 2020  |  4 minutes  |  662 mots  |  Hachette, TS

Documents Affaiblissement des signaux « Un courant électrique passant au travers d’un conducteur dissipe une partie de son énergie sous forme de chaleur (pertes par effet Joule). Il en résulte une diminution de la puissance de ce signal. Les pertes augmentent avec la résistance du câble. La résistance est elle-même fonction de la longueur du câble, de son diamètre et de sa résistivité1 […] Les technologies xDSL2 font passer des signaux électriques à haute fréquence dans les câbles téléphoniques, constitués de fils de cuivre. [Lire]
Absorption  Atténuation  Ondes  Fibre optique 

Évaluer l'atténuation du signal dans une fibre optique

 Publié le September 18, 2020  |  2 minutes  |  326 mots  |  David Latreyte

Exercice La puissance lumineuse d’un signal transmis par une fibre optique décroît avec la distance qu’il parcourt. Le coefficient d’atténuation linéique $\alpha$ caractérise cette décroissance. ll est défini par la relation : $$ \alpha = \dfrac{10}{L} \, \log \left( \dfrac{ \cal I_e }{ \cal I_s } \right) $$ $\alpha$ est exprimé en décibel par unité de longueur ($\pu{dB/m}$), $L$ est la longueur de la fibre en mètre, $\cal I_e$ et $\cal I_s$ sont respectivement les intensités en entrée et en sortie du signal. [Lire]
Absorption  Atténuation  Ondes  Fibre optique