Mécanique

Problématique

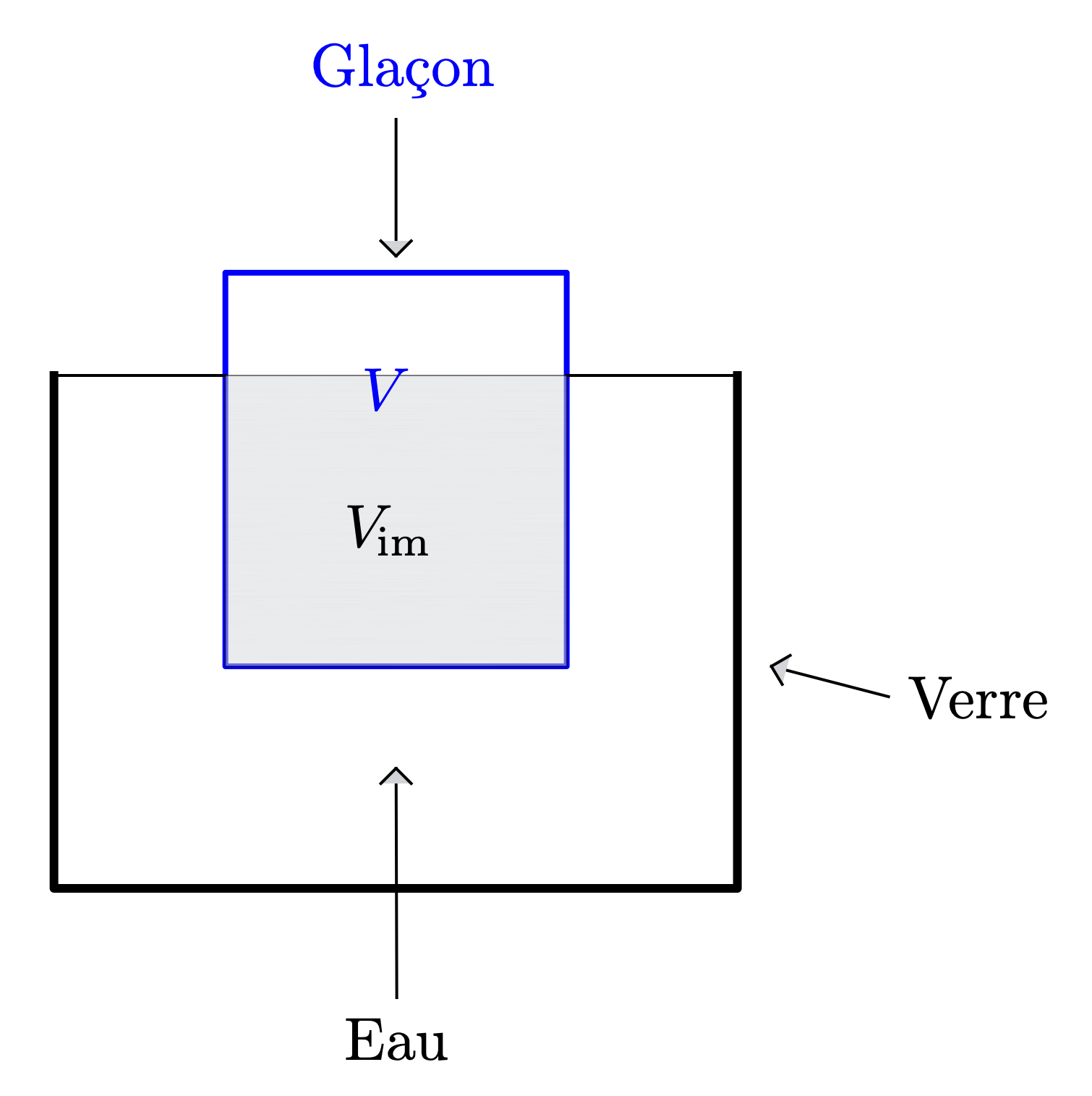
On introduit un glaçon dans un verre d’eau et on ajoute de l’eau liquide de telle sorte que cette dernière affleure.

Que va-t-il se passer à la fonte du glaçon ? L’eau va-t-elle déborder du verre ?

Données

On note

• $V_g$ le volume du glaçon et $V_{im}$ le volume immergé du glaçon ;
• $\rho_l$ la masse volumique de l’eau liquide et $\rho_g$ la masse volumique de l’eau solide ;
• $V_f$ le volume occupé par l’eau initialement sous forme de glace une fois transformée en liquide ;
• On néglige la poussée d’archimède qui s’exerce sur la partie émergée du glaçon ;
• On note $g$ l’accélération du champ de pesanteur.

Résolution du problème

1. Lorsque du changement de phase du glaçon $$ \ce{H2O (sol) –> H2O (liq)} $$ y a-t-il conservation de la quantité de matière d’eau (du glaçon) ?

Les effets de marée sont fréquemment cités. On les invoque, par exemple, pour expliquer la nature particulaire des anneaux de Saturne ou pour récuser telle hypothèse sur la formation des planètes.

Si l’on considère un point matériel, soumis aux seules actions gravitationnelles, son accélération $\vec{a} (M)$ au point $M$ relativement à un référentiel galiléen, est :

$$ \vec{a} (M) = \overrightarrow{G} (M) $$

où $\overrightarrow{G} (M)$ est le champ gravitationnel en $M$. De façon tout à fait extraordinaire, cette accélération est indépendante de la masse du corps ! C’est, sous une forme plus générale, la fameuse loi de chute des corps : dans le vide, tous les corps tombent également vite . Cette simplicité fondamentale est bien connue de tous, mais peut-être n’en tire-t-on pas suffisamment les conséquences. L’impesanteur est l’illustration évidente de la propriété précédente. Supposons, par exemple, un vaisseau spatial en mouvement sous l’action des seules forces gravitationnelles. Si le mouvement du vaisseau est une translation d’accélération $\vec{a}$ (relativement à un référentiel galiléen), dans un champ de gravitation uniforme $\overrightarrow{G}$, on a :