Concentrations massique et molaire
Qu’est-ce qu’une solution ?
Exercice
On réalise une solution aqueuse de permanganate de potassium en introduisant $m = \pu{0,79 g}$ de permanganate de potassium solide, $\ce{KMnO4}$, dans $V_{0} = \pu{250 mL}$ d’eau distillée. On note $(S_0)$ cette solution et on suppose que la dissolution s’effectue sans effet de volume.
- Le permanganate de potassium est le soluté. Qu’est-ce cela signifie ?
Réponse
Un soluté est une espèce chimique ou un ensemble d’espèces chimiques que l’on dissout dans un solvant.
La quantité de matière d’un soluté est très inférieure à la quantité de matière du solvant.
- L’eau est le solvant. Qu’est-ce cela signifie ?
Réponse
Un solvant est une substance liquide qui a la propriété de dissoudre d’autres
substances introduites en petites quantités.
Nous apprendrons cette année pourquoi les solvants possèdent cette propriété.
- Utiliser les mots « homogène », « soluté », « solvant » pour expliquer ce qu’est une solution.
Réponse
Une solution est un mélange homogène résultant de la dissolution d’un soluté dans un solvant.
- Qu’est-ce qu’une solution aqueuse ?
Réponse
Une solution aqueuse est une solution dont le solvant est l’eau.
Qu’est-ce que la concentration massique en soluté d’une solution ?
Exercice (suite)
La concentration massique en permanganate de potassium de la solution préparée est égale à $C_{0_m} = \pu{3,2 g.L-1}$ (ou $C_{0_m} = \pu{3,2 g/L}$).
- Qu’appelle-t-on concentration massique en soluté d’une solution ?
Réponse
La concentration massique en soluté d’une solution est la masse de ce soluté dissoute par unité de volume de la solution. Elle s’exprime en $\pu{g/L}$ (en chimie).
- En raisonnant à partir des unités, indiquer comment on peut calculer la concentration massique en soluté, lorsqu’on connaît la masse $m$ de soluté dissoute et le volume $V$ de la solution.
Réponse
$$C_m = \dfrac{m}{V}$$
- Appliquer l’expression de la concentration massique en soluté pour retrouver la concentration massique en permanganate de potassium annoncée dans l’exercice.
Réponse
- $C_m = \dfrac{ m(\ce{KMnO4}) }{V}$
- A.N. $C_m = \dfrac{ \pu{0,79 g} }{ \pu{250e-3 L} } = \pu{3,2 g/L}$.
Qu’est-ce que la concentration molaire en soluté d’une solution ?
Exercice (suite)
La concentration molaire en permanganate de potassium de la solution préparée est égale à $C_{0} = \pu{2,0e-2 mol.L-1}$ (ou $C_{0} = \pu{2,0e-2 mol/L}$).
- Qu’appelle-t-on concentration molaire en soluté d’une solution ?
Réponse
La concentration molaire en soluté d’une solution est la quantité de matière de ce soluté dissoute par unité de volume de la solution. Elle s’exprime en $\pu{mol/L}$ (en chimie).
- En raisonnant à partir des unités, indiquer comment on peut calculer la concentration molaire en soluté, lorsqu’on connaît la quantité de matière $n$ de soluté dissoute et le volume $V$ de la solution.
Réponse
$$C = \dfrac{n}{V}$$
- Appliquer l’expression de la concentration molaire en soluté pour retrouver la concentration molaire en permanganate de potassium annoncée dans l’exercice, a masse molaire du permanganate de potassium étant égale à $M(\ce{KMnO4}) = \pu{158 g/mol}$.
Réponse
- $C = \dfrac{n(\ce{KMnO4})}{V}$ et $n(\ce{KMnO4}) = \dfrac{m(\ce{KMnO4})}{M(\ce{KMnO4})}$, donc $C = \dfrac{ m(\ce{KMnO4}) }{ M(\ce{KMnO4}) \, V }$
- A.N. $ C = \dfrac{ \pu{0,79 g} }{ \pu{158 g/mol} \times \pu{250e-3 L} } = \pu{2,0e-2 mol/L} $.
Quelle est la relation entre les concentrations massique et molaire d’un soluté en solution ?
- Déterminer la relation algébrique qui lie la concentration massique en soluté $C_m$ et la concentration molaire en soluté $C$.
Réponse
- $C = \dfrac{n}{V}$ et $n = \dfrac{m}{M}$ donc $C = \dfrac{m}{M\, V} = \dfrac{m}{V} \dfrac{1}{M}$.
- Comme $C_m = \dfrac{m}{V}$, $$ C = \dfrac{C_m}{M}$$
En résumé
- La concentration massique en soluté d’une solution est la masse de ce soluté dissoute par unité de volume de la solution. Elle s’exprime en $\pu{g/L}$ (en chimie) et se calcule grâce à l’expression : $$C_m = \dfrac{m}{V}$$
- La concentration molaire en soluté d’une solution est la quantité de matière de ce soluté dissoute par unité de volume de la solution. Elle s’exprime en $\pu{mol/L}$ (en chimie) et se calcule grâce à l’expression : $$C = \dfrac{n}{V}$$
Dilution
Qu’est-ce qu’une dilution ?
Exercice (suite)
On ajoute à la solution $(S_{0})$ de l’exercice un volume $V_{1} = \pu{250 mL}$ d’eau. La nouvelle solution formée est notée $(S_{1})$.
- La quantité de matière de permanganate de potassium a-t-elle varié au cours de cette expérience ?
Réponse
Comme on a ajouté de l’eau, la quantité de matière de permanganate de potassium n’a pas varié.
- Calculer la quantité de matière du permanganate de potassium apporté (c’est à dire introduit) dans la solution.
Réponse
- $n(\ce{KMnO4}) = \dfrac{n(\ce{KMnO4})}{M(\ce{KMnO4})}$
- A.N. $n(\ce{KMnO4}) = \dfrac{ \pu{0,79 g} }{ \pu{158 g/mol} } = \pu{5,0e-3 mol}$.
- La concentration molaire en permanganate de potassium a-t-elle varié au cours de cette expérience ?
Réponse
Le volume de la solution a augmenté alors que la quantité de matière en soluté est restée constante. La concentration en soluté a diminué.
- Calculer la concentration molaire $C_{1}$ en permanganate de potassium de la solution $(S_{1})$.
Réponse
- $C_{1} = \dfrac{n(\ce{KMnO4})}{ V_{\text{total}}}$
- A.N. $C_{1} = \dfrac{ \pu{5,0e-3 mol} }{ \pu{(250 + 250)\cdot 10^{-3} L}} = \pu{1,0e-2 mol/L}$
- Après comparaison des concentrations molaires $C_0$ et $C_1$ en permanganate de potassium apporté, indiquer quelle est l’action d’une dilution sur les concentrations.
Réponse
$C_0 > C_1$. Une dilution est donc un processus visant à diminuer la concentration d’une espèce chimique.
En résumé
Une dilution est un processus visant à obtenir une solution finale (appelée solution fille) dans laquelle la concentration en soluté est inférieure à celle de la solution initiale (appelée solution mère).
- soit par ajout de solvant directement dans la solution mère (qui est alors perdue);
- soit par prélèvement d’une partie de la solution mère que l’on complète avec le solvant dans un nouveau récipient (tube à essais, fiole jaugée, etc.). Cette méthode préserve la solution mère.
Comment détermine-t-on le volume de solution mère à prélever lors d’une solution ?
Exercice (suite)
On prélève un volume $V_{p} = \pu{20 mL}$ de la solution $(S_{0})$ à l’aide d’une pipette jaugée. On introduit ce volume de solution dans une fiole jaugée de $\pu{100 mL}$. On complète jusqu’au trait de jauge par de l’eau distillée. On a alors formé la solution $(S_{2})$, de volume $V_{2} = \pu{100 mL}$.
- Identifier les solutions mère et fille.
Réponse
$(S_{0})$ est la solution mère, $(S_{2})$ est la solution fille}.
- Quelle quantité de matière de permanganate de potassium a été prélevée dans la solution mère ?
Réponse
- $n_{p} = C_{0} \times V_{p}$.
- A.N. $n_p = \pu{2,0e-2 mol/L} \times \pu{20e-3 L} = \pu{4,0e-4 mol}$.
- Quelle quantité de matière de permanganate de potassium est présente dans la solution fille ?
Réponse
$n_2 = n_p$ puisque toute la quantité de matière prélevée dans la solution mère a été introduite dans la solution fille.
- En déduire la concentration en permanganate de potassium dans la solution fille.
Réponse
$C_2 = \dfrac{ n_2 }{ V_2 }$ donc $C_2 = \dfrac{ \pu{4,0e-4 mol} }{ \pu{100e-3 L} } = \pu{4,0e-3 mol/L}$.
- Par combien la concentration en permanganate de potassium a-t-elle été divisée ?
Réponse
La concentration en permanganate de potassium a été divisée par cinq.
- Que représente le volume $V_p$ comparativement au volume $V_2$ ?
Réponse
Le volume $V_p$ représente le cinquième du volume $V_2$.
En résumé
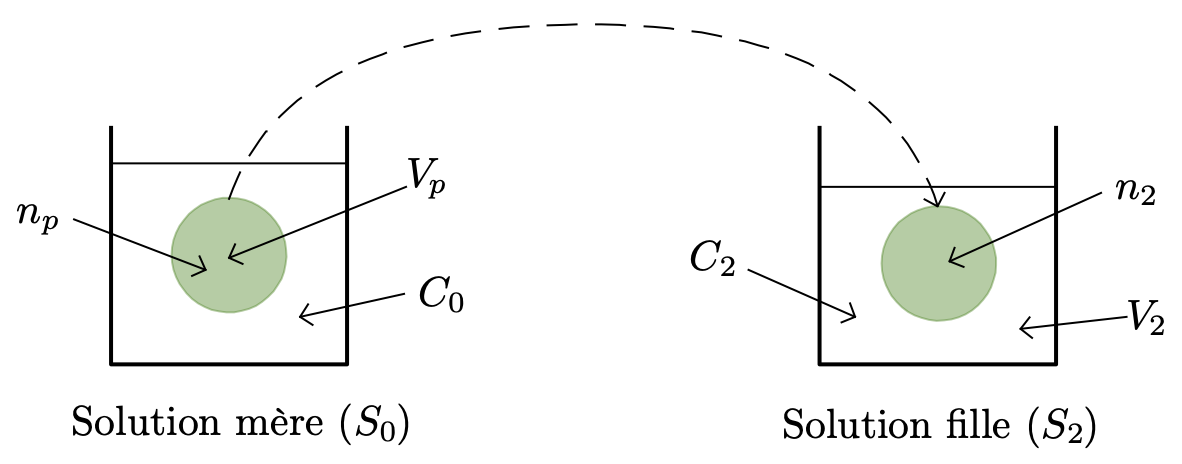
- La quantité de matière prélevée dans la solution mère est : $n_p = C_0 V_p$ ;
- La quantité de matière en soluté dans la solution fille est : $n_2 = C_2 V_2$ ;
- Le soluté dans la solution fille a pour origine le prélèvement dans la solution mère, donc : $n_p = n_2$.
Donc $$ C_0 V_p = C_2 V_2 $$