Point mathématique : le logarithme décimal
Logarithme
Le logarithme décimal est la fonction réciproque de la fonction $f$ telle que $f(x) = 10^x$ : $$ \forall x>0, y = \log (x) \Leftrightarrow x = 10^y $$ Le logarithme décimal est une fonction croissante et continue. De plus, $$ \lim_{x \to 0^+} = -\infty \text{ et } \lim_{x \to \infty} = +\infty $$
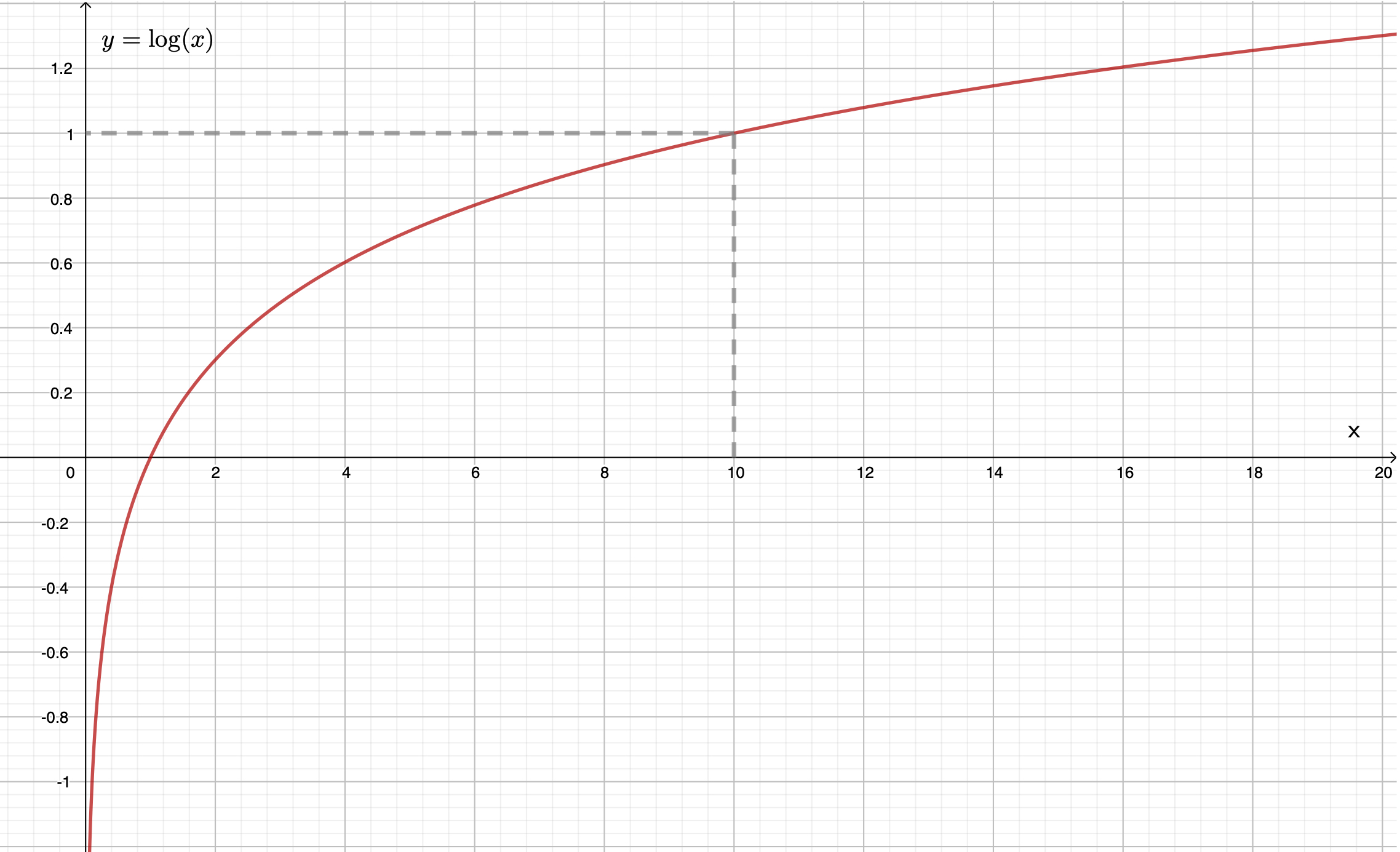 > Graphique de la fonction « logarithme décimal »
> Graphique de la fonction « logarithme décimal »
- Commenter l’évolution de la pente de la tangente à la fonction « logarithme décimal » lorsque la valeur de la variable $x$ augmente.
Réponse
La pente, ou coefficient directeur, de la tangente diminue lorsque la variable $x$ augmente.
[Lire]