-
Pour s’échauffer : n° 8, 9, 10
-
Célérité et retard : n° 14, 15, 16
-
Les ondes périodiques : n° 17, 18, 19
-
Entraînement : n° 26, 28
-
Pour aller plus loin : n° 32, 34, 36
Qu'est-ce qu'une onde mécanique progressive ?
À l’issue de cette séance vous devriez être capables d’expliquer ce qu’est une onde mécanique progressive et de citer quelques unes des caractéristiques des ondes mécaniques.
Qu’est-ce qu’une onde mécanique ? Onde se propageant le long d’une corde On dispose, sur le sol, une corde tenue à l’une de ses extrémités. Avec la main, on imprime rapidement à l’extrémité libre de cette corde un bref mouvement vers le haut puis vers le bas.
[Lire]
Utilisation d'un tableur pour déterminer une incertitude de mesure de type A
Problème Un groupe d’élèves effectue la mesure de la célérité des ultrasons dans l’air dans une pièce à $\pu{20 °C}$. Leurs résultats sont regroupés dans le tableau ci-dessous :
N° mesure Valeur ($\pu{m/s}$) N° mesure Valeur ($\pu{m/s}$) 1 338 11 338 2 341 12 336 3 338 13 342 4 340 14 341 5 337 15 337 6 339 16 342 7 342 17 336 8 338 18 338 9 340 19 339 10 339 20 343 À partir des mesures obtenues, évaluer la célérité des ultrasons dans l’air à $\pu{20 °C}$ en calculant l’incertitude de répétabilité avec un niveau de confiance de 95 % puis à 99 %.
[Lire]
Détermination pratique des incertitudes
Avertissement Aucune des formules présentées dans ce document ne doit être apprise par cœur car elles seront systématiquement données si nécessaire.
En revanche, il faudra être capable de choisir la formule à utiliser et il sera impératif de savoir l’utiliser.
Le résultat d’une mesure n’est pas une valeur mais un intervalle de valeurs, que l’on note $\pu{m±U(m)}$1, dans lequel on peut considérer, avec un certain niveau de confiance, que la « valeur vraie » se trouve.
[Lire]
Incertitudes et analyse des erreurs dans les mesures physiques
La physique est une science naturelle. Les lois qui décrivent et qui prédisent le comportement des objets doivent être validées par l’expérience et donc par la publication de résultats de mesures (à partir desquelles on peut être amené à effectuer des calculs).
Dans ce document on va se poser les questions suivantes, sans répondre complètement à la seconde :
Quelle valeur a-t-on réellement mesuré ? Quelle confiance peut-on accorder à cette mesure ?
[Lire]
Exercices et Annale
Livre scolaire 32, 34, 33 pages 509 et 510 Solutions Fichier au format pdf
Annale Autour du papillon Ne pas traiter les première et deuxième partie (seulement la partie 3).
D'où viennent les couleurs des ailes des papillons ? Correction de l'annale 1.1.1. Les chauve-souris émettent des ondes dont la fréquence est $f_e = \pu{50 kHz}$. L’homme peut entendre les sons dont les fréquences sont comprises entre $\pu{20 Hz}$ et $\pu{20 kHz}$.
[Lire]
Conditions d’interférence de deux ondes sinusoïdales
Interférences On appelle interférence le résultat de la superposition de plusieurs ondes (mécaniques ou électromagnétiques) en un même point de l’espace.
En physique, on distingue normalement deux phénomènes particuliers qui se produisent lorsqu’on additionne des ondes sinusoïdales :
L’interférence, quand les ondes ont la même fréquence. Le battement, quand les fréquences des ondes sont légèrement différentes. Par la suite, toutes les ondes étudiées seront sinusoïdales, de même fréquence $f$.
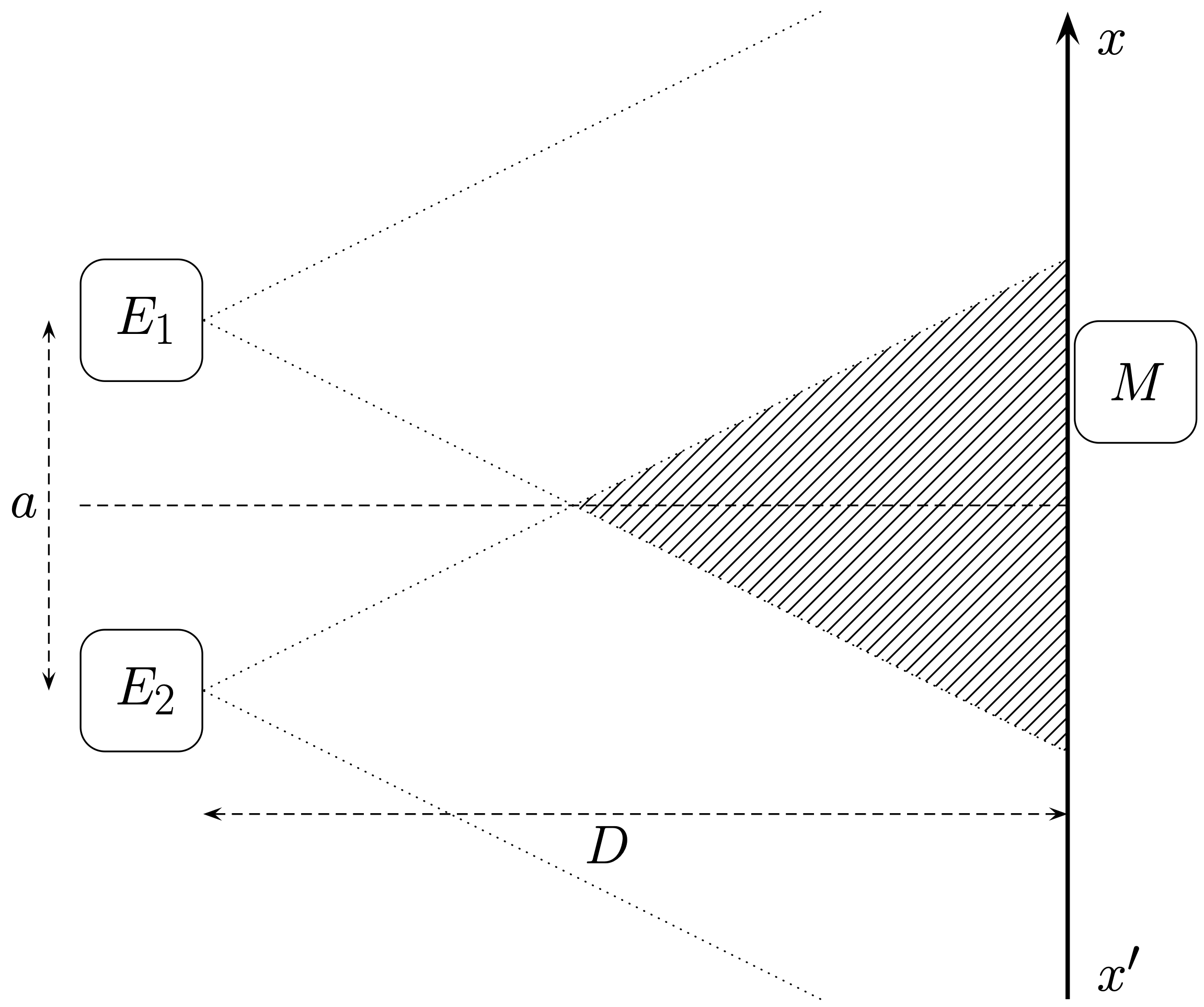
Un exemple de montage d’étude d’une figure d’interférence Schéma de principe Deux ondes sinusoïdales de même fréquence $f$ sont émises par les deux émetteurs $E_1$ et $E_2$.
[Lire]
Différence de marche et conséquence sur la superposition de deux ondes synchrones
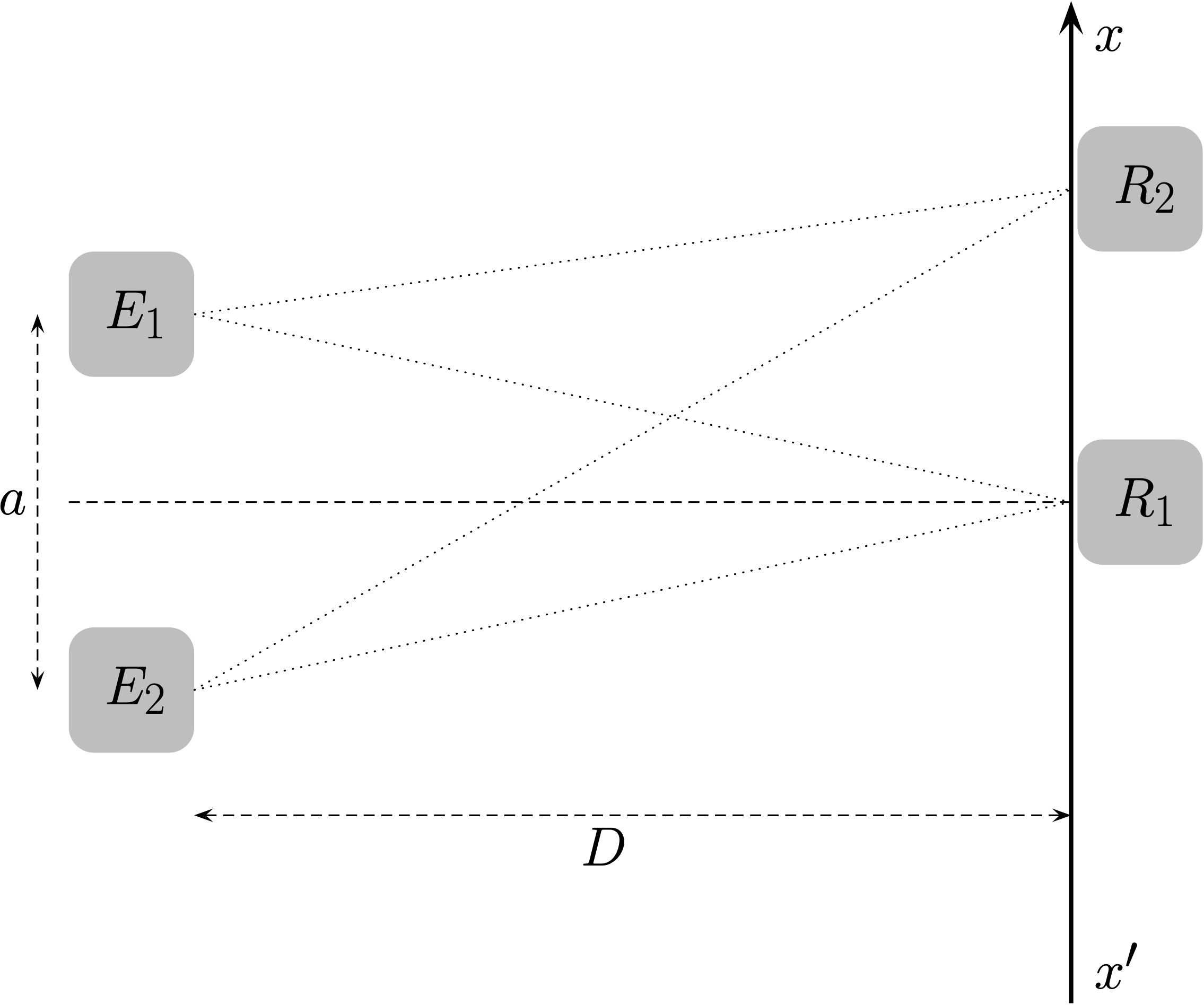
Émission de bips sonores par deux émétteurs Deux émetteurs synchronisés, $E_1$ et $E_2$, émettent chacun un bip sonore, à la date $t=\pu{0 s}$ alors qu’un récepteur $R$ se trouve à la position $R_1$.
Combien de bips perçoit le récepteur ? Pourquoi ? Réponse 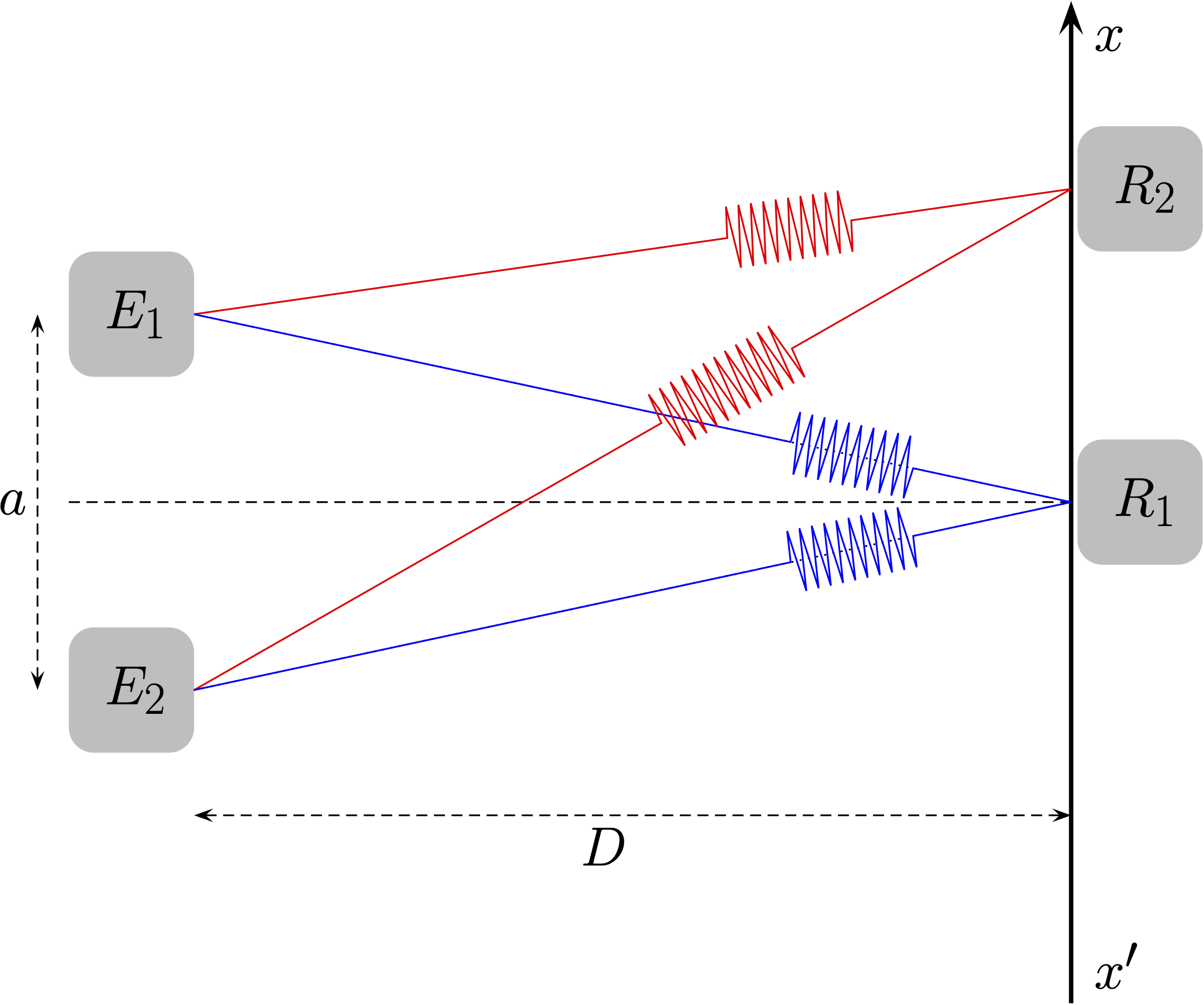Le récepteur perçoit un seul bip puisque les deux signaux doivent parcourir la même distance à la même vitesse (car ils se propagent dans le même milieu) et arrivent donc à la même date.
[Lire]
Retard, déphasage d'une onde sonore sinusoïdale
Deux élèves, lors d’une séance de travaux pratiques, réalisent l’expérience suivante. Ils branchent un générateur basse fréquence délivrant une tension sinusoïdale aux bornes d’un haut-parleur. À l’aide de deux microphones identiques reliés à une carte d’acquisition, ils visualisent les signaux électriques $u_1 (t)$ et $u_2 (t)$ produits lors de la réception du son (figures 1 et 2). Les deux microphones $M_1$ et $M_2$ sont séparés par une distance $d$.
Schématisation du montage Figure 1 Figure 2 Donnée La vitesse du son dans les conditions de l’expérience est de $\pu{340 m/s}$.
[Lire]
Utiliser le réseau téléphonique pour surfer sur Internet
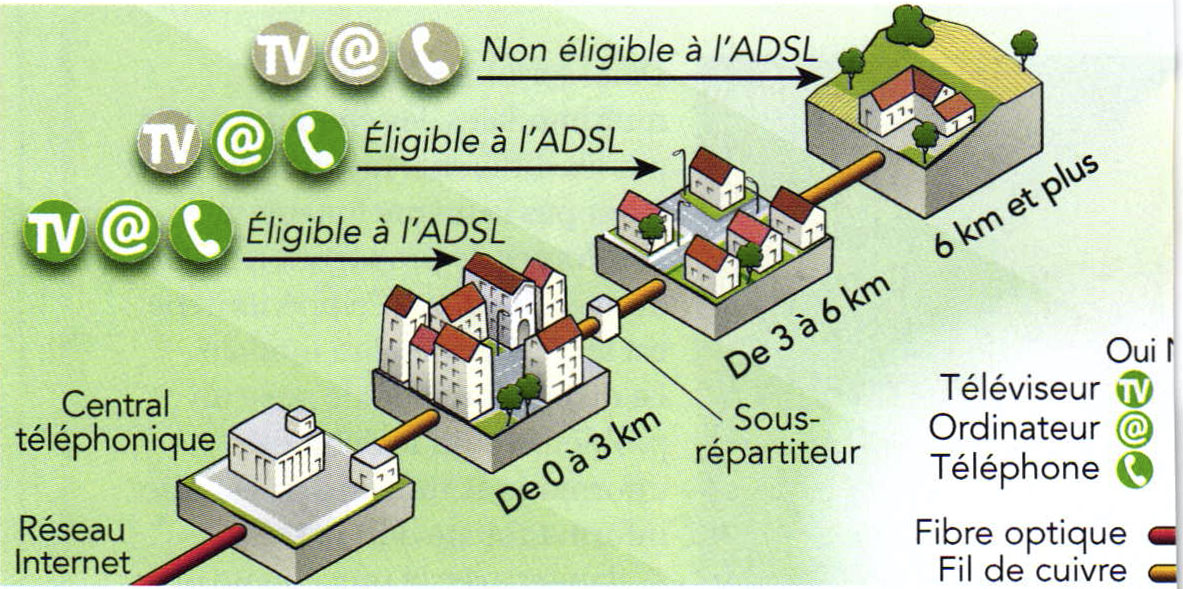
Documents Affaiblissement des signaux « Un courant électrique passant au travers d’un conducteur dissipe une partie de son énergie sous forme de chaleur (pertes par effet Joule). Il en résulte une diminution de la puissance de ce signal. Les pertes augmentent avec la résistance du câble. La résistance est elle-même fonction de la longueur du câble, de son diamètre et de sa résistivité1 […] Les technologies xDSL2 font passer des signaux électriques à haute fréquence dans les câbles téléphoniques, constitués de fils de cuivre.
[Lire]