« La spectrométrie de masse est une technique d’analyse permettant notamment d’identifier des molécules organiques et de déterminer leur formule développée. Dans un spectromètre de masse, des ions sont séparés en fonction de leur masse et de leur charge électrique.
Le Canadien Arthur Dempster (1886–1950) a contribué à développer cette technique durant la première moitié du XXème siècle et ses travaux l’ont conduit à la découverte de l’isotope 235 de l’uranium (seul l’isotope 238 était connu à l’époque), utilisé comme combustible fissile dans les centrales nucléaires. Cette technique ne nécessitant que des microéchantillons est aussi utilisée dans l’analyse d’œuvres d’art, ainsi qu’en imagerie biomédicale... »
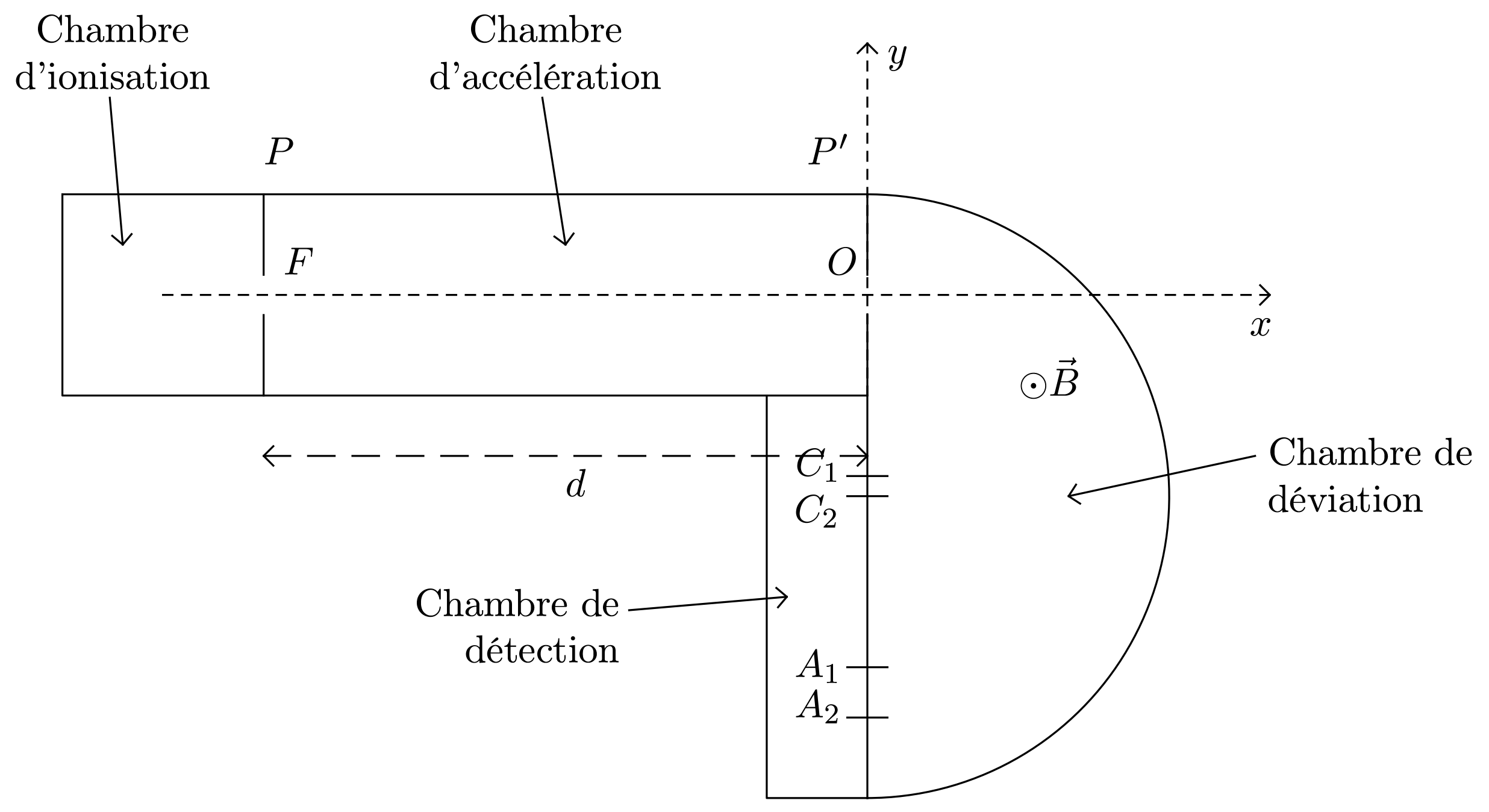
Le principe du spectromètre de masse est illustré dans cet exercice dans le cas de la détermination de l’abondance isotopique relative en $\ce{_6^{12}C}$ et $\ce{_6^{13} C}$, employée dans le domaine alimentaire, en répression des fraudes.
-
Un vide poussé est maintenu dans tout l’appareil.
-
L’échantillon à analyser subit une série de transformations afin que tout le carbone se retrouve combiné sous forme de dioxyde de carbone $\ce{CO2}$.
-
Dans la chambre d’ionisation, les molécules de dioxyde de carbone sont bombardées par des électrons. Il se forme les cations $\ce{_6^{12} CO2^+}$ et $\ce{_6^{13} CO2^+}$.
-
Ces cations sortent de la fente $F$ avec une vitesse négligeable dans le référentiel terrestre du laboratoire.
-
Dans la chambre d’accélération, délimitée par les plaques $P$ et $P’$ distantes de $d$ mètres, règne un champ électrostatique uniforme $\vec{E}$, de direction perpendiculaire aux plaques $P$ et $P’$. Les cations sont accélérés et, en $O$, possèdent respectivement des vitesses $\vec{v}_{01}$ et $\vec{v}_{02}$.
-
Dans la chambre de déviation, on sépare ces ions avant leur entrée dans la chambre de détection à l’aide d’un champ magnétique uniforme $\vec{B}$, de direction perpendiculaire au plan de la figure 1.
Données
- Unité de masse atomique : $\pu{1 u} = \pu{1,660538921e27 kg/nucléon}$ ;
- Charge électrique fondamentale : $e = \pu{1,6e-19 C}$
- Tension $U$ entre les armatures $P$ et $P’$ : $U = \pu{3,9e3 V}$ ;
- Longueur de la chambre d’accélération : $d = \pu{0,5 m}$ ;
- Valeur du champ magnétique : $B = \pu{0,12 T}$.
Mouvement des cations dans la chambre d’accélération
-
Dans quel sens doit être orienté le champ électrique $\vec{E}$ de façon à ce que les cations soient accélérés de $F$ à $O$ ?
Justifier la réponse. -
Calculer les masses respectives $m_1$ et $m_2$ des ions $\ce{_6^{12} CO2^+}$ et $\ce{_6^{13} CO2^+}$
Pour l’oxygène, seul l’isotope $\ce{^{16} O}$ sera considéré. -
Démontrer que le poids des cations est négligeable comparé à la force électrique à laquelle ils sont soumis. On négligera systématiquement le poids des électrons dans le suite de ce problème.
-
Par application des lois de Newton déterminer les expressions des vitesses $\vec{v}_{01}$ et $\vec{v}_{02}$ en fonction de $e$, $U$, $m_1$ ou $m_2$. Détailler le raisonnement.
-
Pourquoi l’utilisation de la relativité restreinte ne s’impose-t-elle pas dans ce problème ?
Mouvement des cations dans la chambre de déviation
Dans la chambre de déviation les ions subissent une force résultant de l’interaction avec le champ magnétique $\vec{B}$, appelée force de Lorentz $\vec{F}_L$, toujours orthogonale au champ $\vec{B}$ et aux vecteurs vitesse $\vec{v}_{0 i}$ des ions.
Appliquée à un cation $i$ quelconque, elle a pour valeur $F_L = q_i v_i B$ où $q_i$ est la charge du cation, $v_i$ la valeur de sa vitesse et $B$ la valeur du champ magnétique. Dans les conditions de l’expérience, le mouvement des ions s’effectue dans le plan de la figure 1 ; la force de Lorentz est alors dirigée selon le vecteur $\vec{n}$ de la base de Frenet et orientée dans le même sens que ce vecteur. Finalement, le mouvement des ions est circulaire (de centres $C_i$).
-
Rappeler la définition du repère de Frenet.
-
À partir des indications de l’énoncé, donner la forme vectorielle de la force de Lorentz en fonction des vecteurs de la base de Frenet.
-
Démontrer que, puisque le mouvement des cations est circulaire, il est aussi uniforme.
-
Démontrer que la trajectoire d’un cation $i$ a pour rayon $$R_i = \sqrt{\dfrac{2 m_i U}{eB^2}}$$
-
Calculer les valeurs $R_1$ et $R_2$ des rayons des trajectoires des ions $\ce{_6^{12} CO2^+}$ et $\ce{_6^{13} CO2^+}$.
-
Justifier la phrase du paragraphe d’introduction : « Dans un spectromètre de masse, des ions sont séparés en fonction de leur masse et de leur charge électrique ».
-
Les ions $\ce{_6^{12} CO2^+}$ et $\ce{_6^{13} CO2^+}$ atteignent la chambre de détection aux points $A_1$ et $A_2$. Dans cette chambre il n’existe plus aucun champ. Quel est alors le mouvement de ces ions ?
Détermination du temps de vol
On cherche à déterminer la durée du parcours des fragments ionisés $i$ depuis l’entrée dans la chambre d’accélération jusqu’à la sortie de la chambre de déviation (la durée du parcours dans la chambre de détection est négligeable).
-
Montrer que ce « temps de vol » $\Delta t_i$ s’écrit : $$\Delta t_i = d \sqrt{\dfrac{2 m_i}{q_i U}} + \dfrac{\pi m_i}{q_i B}$$
-
Calculer les valeurs des « temps de vol » pour les ions $\ce{_6^{12} CO2^+}$ et $\ce{_6^{13} CO2^+}$.
-
Ces ions sont-ils détectés en même temps ? Lequel arrive le premier ? Justifier ce résultat.