Le protoxyde d’azote est utilisé comme gaz anesthésique en chirurgie. Dans la culture populaire, on emploie souvent l’expression de gaz hilarant. Sa décomposition en phase gazeuse se produit selon le mécanisme réactionnel en deux étapes suivant :
$$\ce{ N2O(g) -> N2(g) + O^{.}(g) }$$ $$\ce{ O^{.}(g) + N2O(g) -> N2(g) + O2(g) }$$
Ici, les concentrations correspondent au rapport entre la quantité de gaz et le volume total de gaz du milieu réactionnel. L’expérience est réalisée avec une concentration initiale en protoxyde d’azote égale à $C_0 = \pu{5,0 mol·L-1}$. La concentration $[\ce{N2}]$ en diazote est relevée toutes les $\pu{0,20 ms}$.
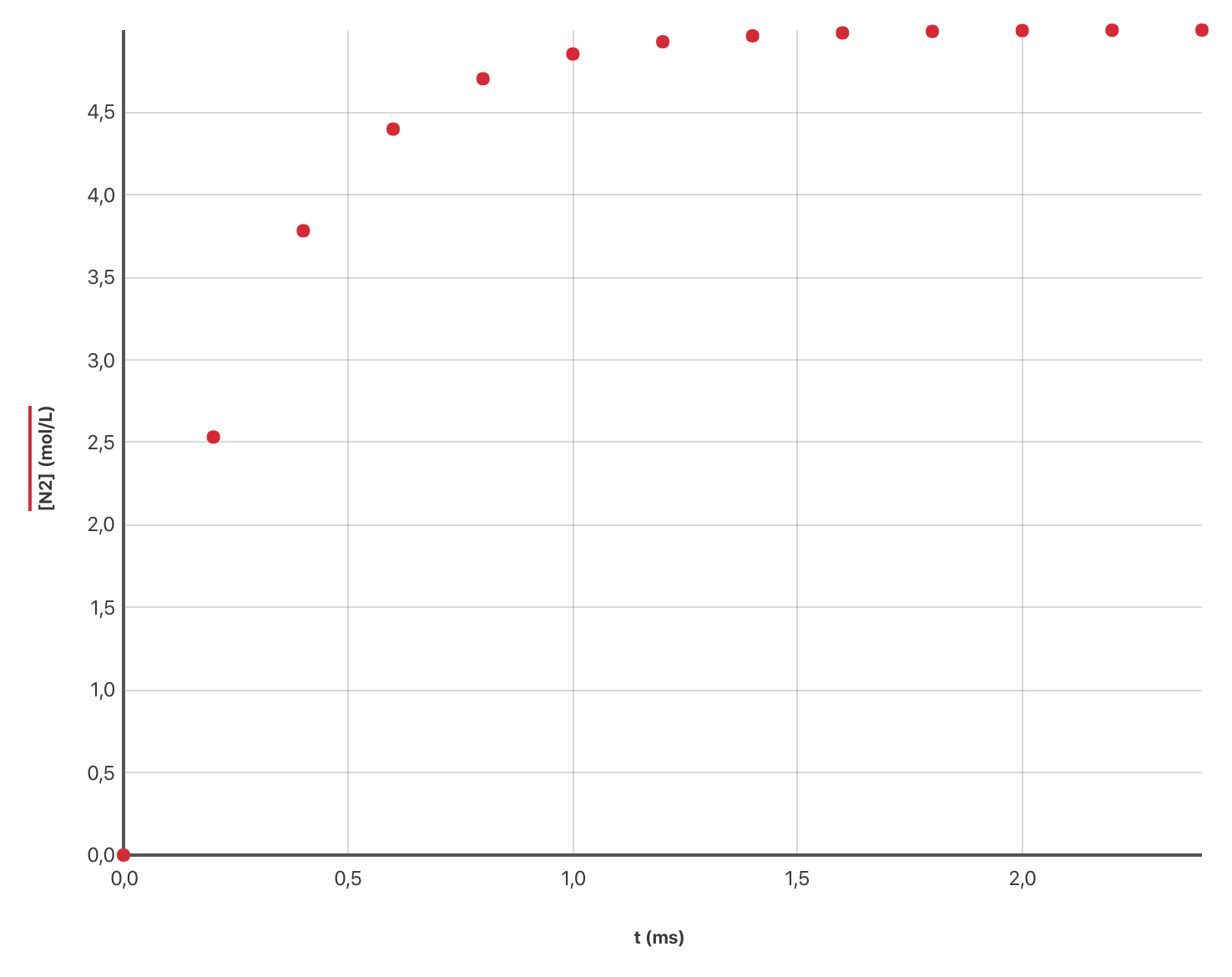
- Identifier les intermédiaires réactionnels apparaissant dans le mécanisme réactionnel.
Réponse
Le radical $\ce{O^{.}(g)}$ est un intermédiaire réactionnel, car il est formé dans la première étape, puis consommé dans la seconde.
- Écrire l’équation-bilan.
Réponse
$\ce{ 2 N2O(g) -> 2 N2(g) + O2(g) }$
-
Dresser le tableau d’avancement de la transformation.
-
Dans le tableau, dans le fichier des données ajouter une colonne calculée pour exprimer la concentration $[\ce{N2O}]$ en protoxyde d’azote à chaque instant.
Réponse
$ [\ce{N2O}] = C_0 - 2 x $ et $ [\ce{N2}] = 2x $, donc $ [\ce{N2O}] = C_0 - [\ce{N2}] $.
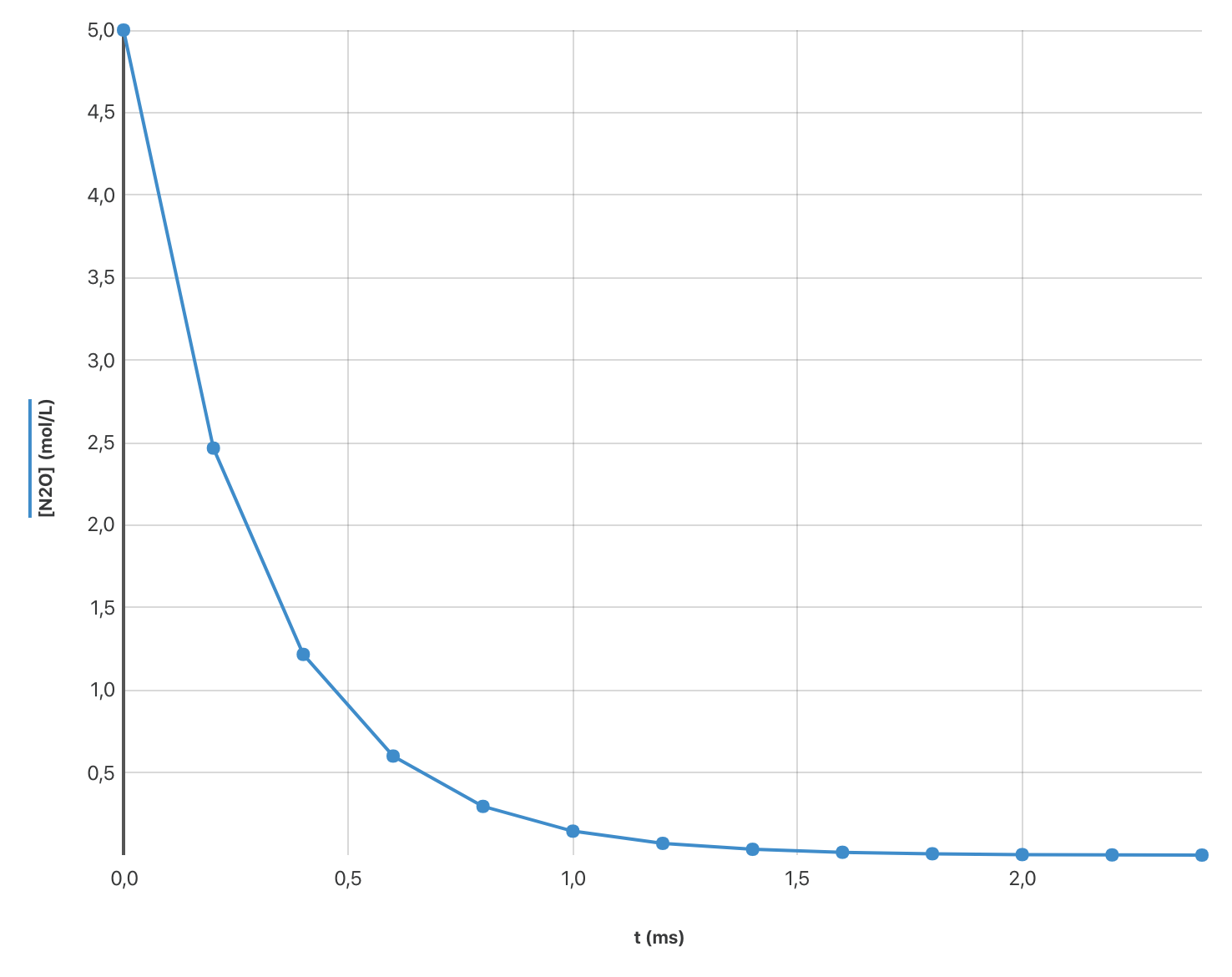
- Exprimer la vitesse volumique de formation $v_f$ de $[\ce{N2}]$.
Réponse
$$ v_f (\ce{N2}) = \dfrac{\mathrm{d} [\ce{N2}]}{\mathrm{dt}} $$
- Trouver la relation qui existe entre la vitesse volumique de formation de $\ce{O2}$, $v_f(\ce{O2})$, et la vitesse volumique de formation de de $[\ce{N2}]$.
Réponse
- $v_f (\ce{N2}) = \dfrac{\mathrm{d} [\ce{N2}]}{\mathrm{dt}}$
- $v_f (\ce{O2}) = \dfrac{\mathrm{d} [\ce{O2}]}{\mathrm{dt}}$
Or, grâce au tableau d’avancement on apprend que $n(\ce{N2})(t) = 2 x(t)$ et $n(\ce{O2})(t) = x(t)$. On en conclut donc que $n(\ce{N2})(t) = 2 n(\ce{O2})(t)$. Il se forme à chaque instant deux fois plus de diazote que de dioxygène.
Finalement, on en déduit que $[\ce{N2}] (t) = 2 [\ce{O2}](t)$ et que $v_f (\ce{N2}) = 2 v_f (\ce{O2}) $.
-
Dans le tableau, dans le fichier des données ajouter deux colonnes calculées pour calculer les vitesses de formation de $\ce{N2}$ et de $\ce{O2}$.
-
Trouver la relation qui existe entre la vitesse volumique de disparition de $\ce{N2O}$, $v_d(\ce{N2O})$, et la vitesse volumique de formation de $\ce{N2}$.
Réponse
- $v_d(\ce{N2O}) = - \dfrac{\mathrm{d} [\ce{N2O}]}{\mathrm{dt}}$.
Or, on a démontré à la question 4. que $ [\ce{N2O}] = C_0 - [\ce{N2}] $, on peut donc écrire, après dérivation par rapport au temps de la relation précédente, que $\dfrac{\mathrm{d} [\ce{N2O}]}{\mathrm{dt}} = - \dfrac{\mathrm{d} [\ce{N2}]}{\mathrm{dt}}$, ce qui implique que $v_d(\ce{N2O}) = v_f(\ce{N2})$.
- Les vitesses volumiques de formation et de disparition sont-elles communes à toutes les espèces chimiques ou dépendent-elles de chaque espèce chimique ?
Réponse
Les vitesses volumiques de formation ou de disparition sont spécifiques à chacune de entités de la réaction. Tout dépend des proportions dans lesquelles ces entités se forment ou disparaissent.
- Dans le tableau, dans le fichier des données ajouter une colonne calculée pour calculer la vitesse de disparition $v_d(\ce{N2O})$ du protoxyde d’azote $\ce{N2O}$ à chaque instant.
Réponse
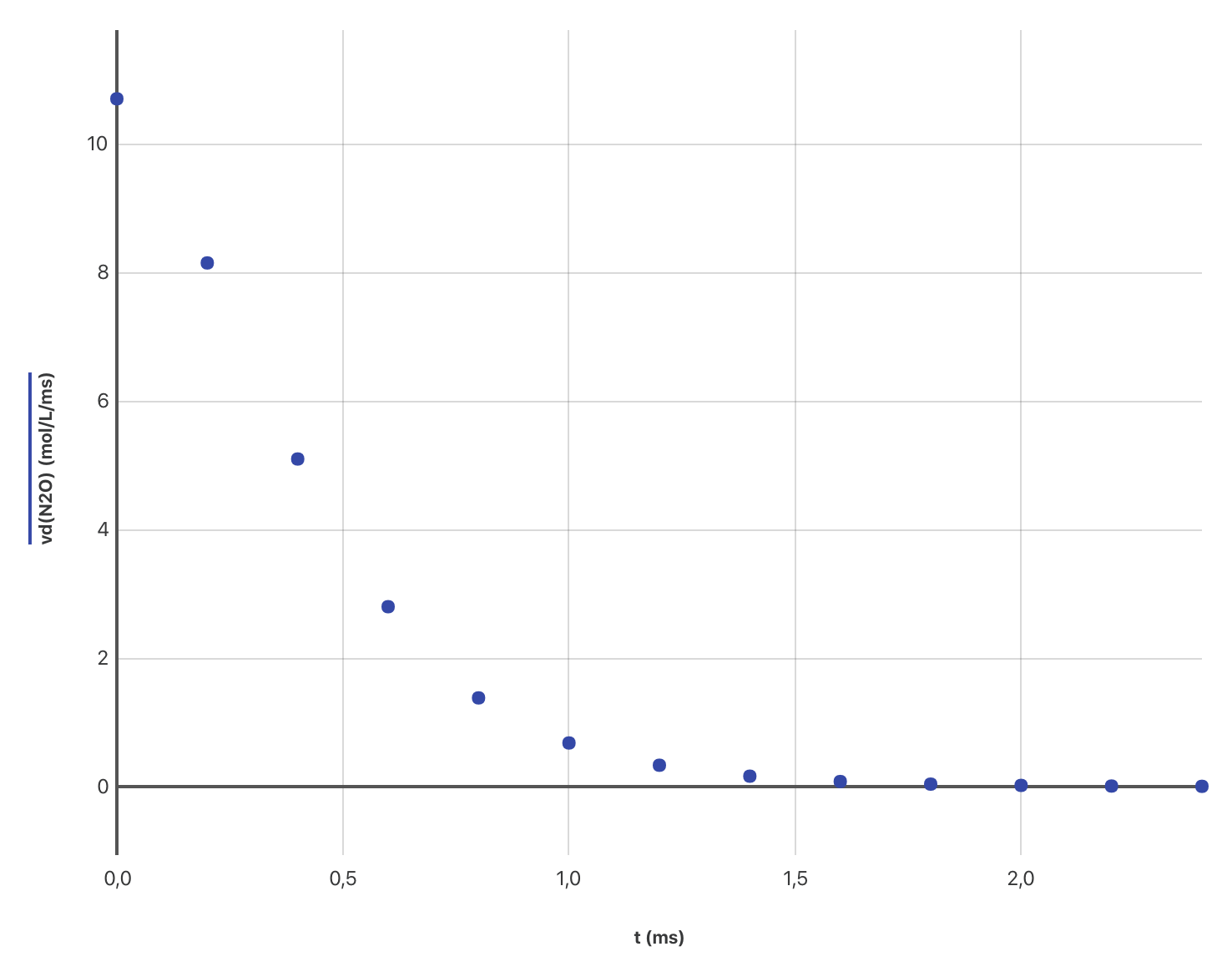
- Tracer l’évolution de la vitesse volumique de disparition de $v_d(\ce{N2O})$ en fonction de $[\ce{N2O}]$. Conclusion.
Réponse
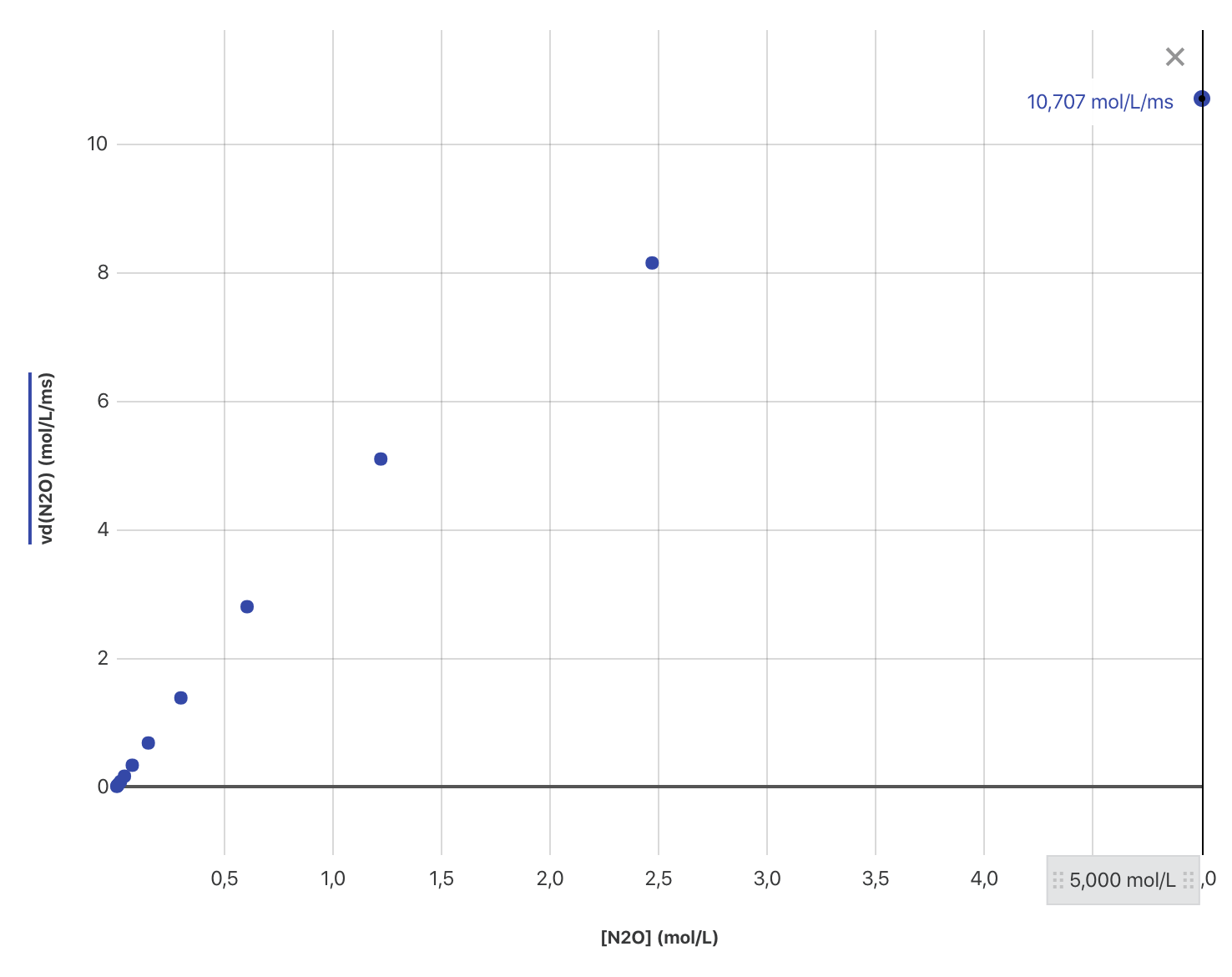
La relation est du type $ v_d(\ce{N2O}) = k [\ce{N2O}]$. La réaction est d’ordre 1 par rapport à la concentration en protoxyde d’azote.