Dessin de figures fractales

Le mot fractale vient du latin fractus qui signifie brisé. En effet, une figure fractale est un objet géométrique infiniment morcelé des détails sont observables à une échelle arbitrairement choisie.

En zoomant sur une partie de la figure, on peut retrouver toute la figure, on dit qu’elle est auto similaire.

http://www.maths-et-tiques.fr/index.php/detentes/les-fractales

http://fr.wikipedia.org/wiki/Fractalehttp://fr.wikipedia.org/wiki/Fractale

Introduction

Dans le code suivant (qu’il faudra étudier et exécuter) :

  1. Quel est le cas de base de l’algorithme récursif ?

  2. Où s’effectue l’appel récursif ?

  3. Pourquoi le cas de base est-il toujours réalisé ?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import turtle
import math as m

def dessine_etoile(t: turtle, pt: tuple, long: int) -> None:
    if long <= 2:
        return None
    
    for i in range(6) :
        x_ext = pt[0] + int(long * m.cos((2 * m.pi / 6) * i))
        y_ext = pt[1] + int(long * m.sin((2 * m.pi / 6) * i))

        pt_ext = (x_ext, y_ext) # Extrémité du segment
        
        t.penup()
        t.setposition(pt)
        
        t.pendown()
        t.setposition(pt_ext)
        
        dessine_etoile(t, pt_ext, long/3)

def main() :
    t = turtle.Turtle()
    t.speed(0)
    t.hideturtle()
    segment = 300
    centre = (0,0)
    dessine_etoile(t, centre, segment)
    turtle.mainloop()
    
main()

Le flocon de von Koch

La première courbe à tracer a été imaginée par le mathématicien suédois Niels Fabian Helge von Koch, afin de montrer que l’on pouvait tracer des courbes continues en tout point, mais dérivables en aucun.

Le principe est le suivant : on divise un segment initial en trois morceaux, et on construit un triangle équilatéral sans base au-dessus du morceau central. On réitère le processus $n$ fois, $n$ étant appelé l’ordre.

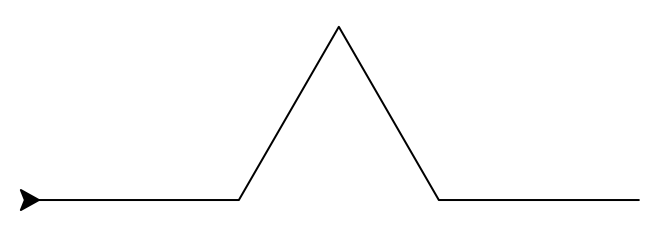
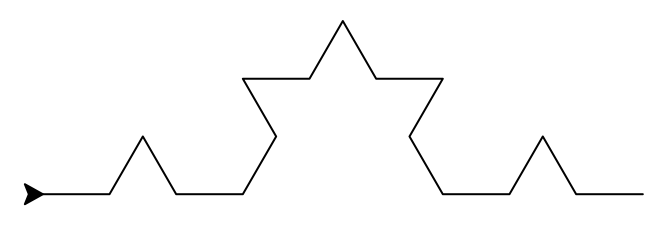
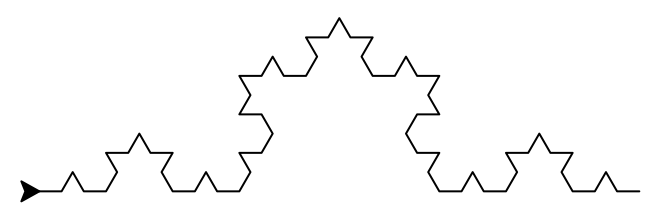
Ordres 0, 1, 2 et 3 de la fractale.

Si on trace trois fois cette figure, on obtient successivement un triangle, une étoile, puis un flocon de plus en plus complexe.

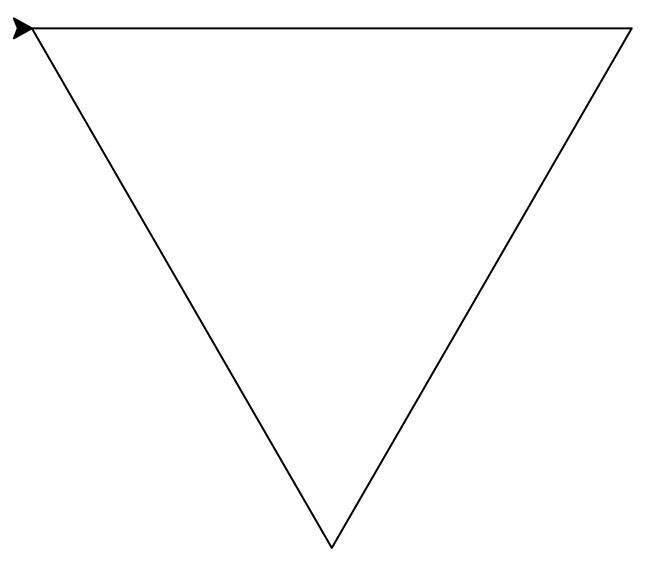
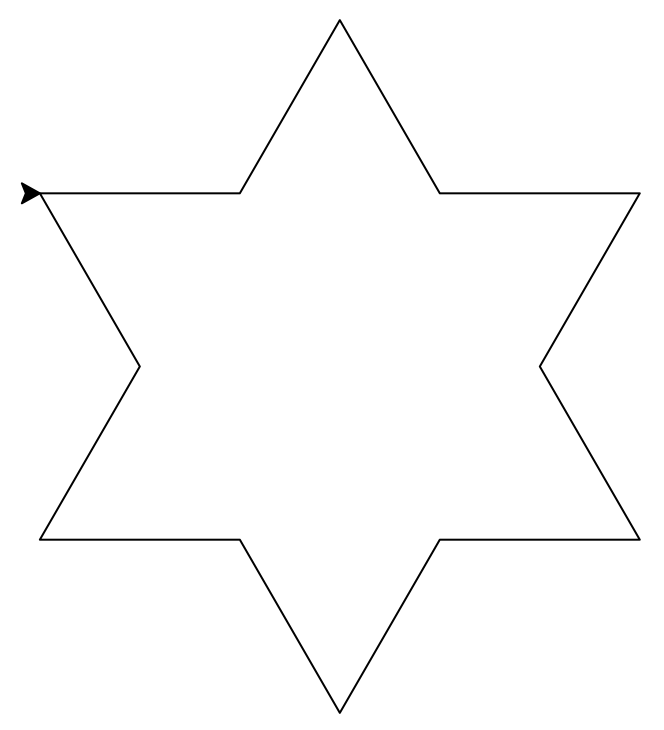
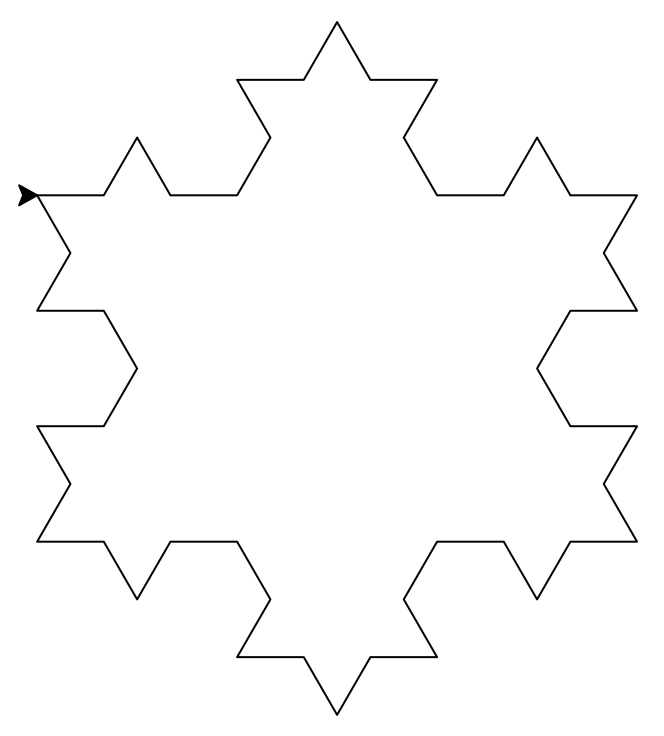
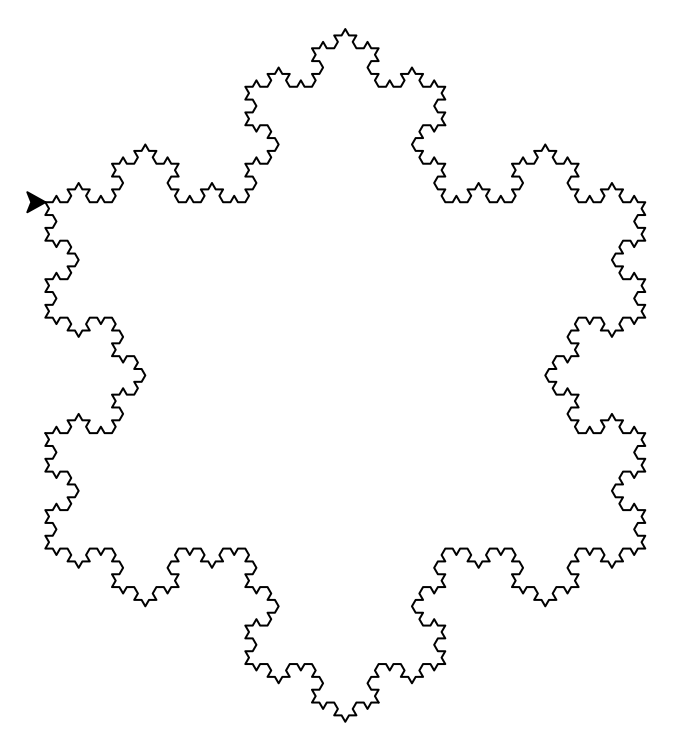
Figures successives (ordre 0, 1, 2 et 4).

Principe de la construction

La méthode de construction utilise un algorithme récursif :

  • À l’ordre 0, il suffit d’appeler une fois la méthode forward pour tracer un segment. C’est le cas de base.

  • À l’ordre 1, il faut appeler la méthode forward (4 fois), les méthodes left et right pour découper le segment en 4 parties (de même longueur).

  • À l’ordre $n \geq 1$, le code ressemble à celui de l’ordre 1, si ce n’est qu’on remplace l’appel de chacune des méthodes forward par le tracé de segments à l’ordre $n-1$. C’est l’appel récursif, on découpe chaque partie de segment en sous-parties.

Travail

  1. Définir la fonction de signature
1

koch_1(t: turtle, l: int) -> None

qui dessine un segment de Koch à l’ordre 1, de longueur $l$, à l’aide de l’objet de type Turtle t. Les sous-segments de la figure sont de longueur $l/3$ et les angles sont de 60 ou 120 degrés.

  1. Définir la fonction main permettant de tester la fonction koch_1.
Remarque.

Les futurs tracés vont nécessiter beaucoup de calculs et l’affichage de nombres points à l’écran. De façon à améliorer la performance,

  • régler la vitesse de la tortue au maximum : t.speed(0) ;

  • cacher le symbole représentant la tortue à l’écran : t.hideturtle.

  1. Définir la fonction de signature
1

koch(t: turtle, n: int, l: int) -> None

qui dessine à l’écran un segment de Koch d’ordre 0 ou 1, de longueur $l$, à l’aide de l’objet de type Turtle t.
Le corps de la fonction doit uniquement gérer les deux cas : $n=0$ et $n=1$ (le cas $n\geq 1$ sera traité dans l’une des prochaines questions.

  1. Modifier la fonction main de façon à tester la fonction koch.

  2. Cette partie généralise la fonction koch au cas $n \geq 2$. Il faut découper chaque segment de droite en sous-parties ; il faut donc remplacer chaque appel de la méthode forward dans koch par un appel de la fonction koch elle-même : koch(t, n-1, ...).
    Trouver par quoi remplacer les … et modifier la fonction.

  3. Tester koch la nouvelle fonction pour une longueur de 300 pixels et $n \in [0, 5]$ (au delà de cette dernière valeur, on ne voit plus trop de différences).

  4. Définir la fonction de signature qui dessine à l’écran un flocon de von Koch, d’ordre $n$ et dont chaque segment à une longueur $l$.

Solution 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

"""
Tracé du flocon de Von Koch
"""
import turtle


def koch_0(t, l):
    """
    koch_0 : Objet[turtle] * Entier/>0/ -> None
    koch_0(t, l) trace à l'écran un segment de longueur l.
    """
    t.forward(l)


def koch_1(t, l):
    """
    koch_1: Objet[turtle] * Entier/>0/ -> None
    koch_1(t, l) dessine une branche de longueur l du flocon de Von Koch à
    l'ordre 1.
    """
    t.forward(l / 3)
    t.left(60)
    t.forward(l / 3)
    t.right(120)
    t.forward(l / 3)
    t.left(60)
    t.forward(l / 3)


def koch(t, n, l):
    """
    koch : Objet[turtle] * Entier/>0/ * Entier/>0/ -> None
    koch(t, n, l) dessine une branche du flocon de Von Koch à
    l'ordre n.
    """
    if n == 0:
        t.forward(l)
    else:
        koch(t, n - 1, l / 3)
        t.left(60)
        koch(t, n - 1, l / 3)
        t.right(120)
        koch(t, n - 1, l / 3)
        t.left(60)
        koch(t, n - 1, l / 3)


def dessine_flocon(t, n, l):
    """
    dessine_flocon : Objet[turtle] * Entier/>0/ * Entier/>0/
                     -> None
    dessine_flocon(t, n, l) dessine un flocon de Von Koch à
    l'ordre n.
    """
    if not t.isdown():
        t.pendown()

    koch(t, n, l)
    t.right(120)
    koch(t, n, l)
    t.right(120)
    koch(t, n, l)
    t.right(120)


def main():
    fen = turtle.Screen()
    fen.bgcolor("black")

    t = turtle.Turtle()
    t.color("white")
    t.speed(0)
    t.hideturtle()
    t.penup()
    t.goto(-150, 150)
    t.pendown()

    dessine_flocon(t, 5, 400)
    #koch(t, 4, 300)

    #koch_1(t, 200)

    fen.exitonclick()


main()

Arbre fractal

On peut appliquer le même principe pour construire d’autre fractales visuellement différentes, mais construites sur le même principe.

Présentation

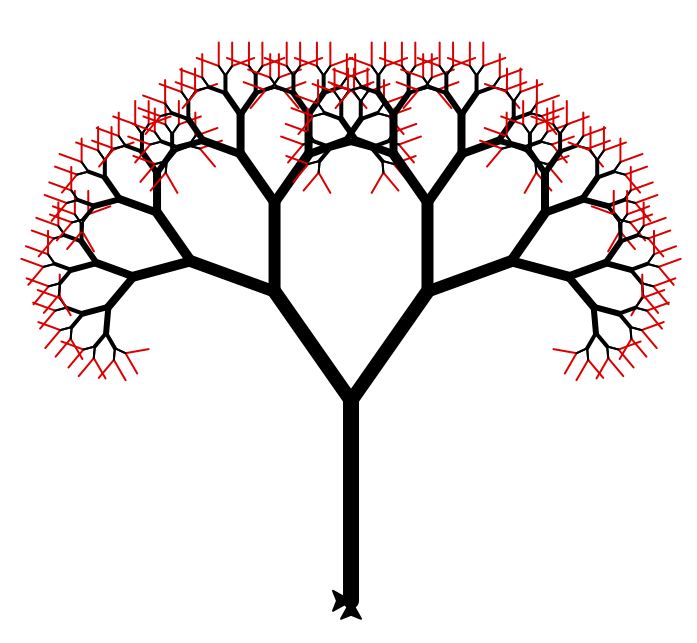> Arbre fractal.

Par exemple, pour construire un arbre, on part d’un segment, et on applique la transformation présentée ci-dessus à chaque segment de la construction (on refait la transformation $n$ fois pour obtenir un arbre d’ordre $n$) :

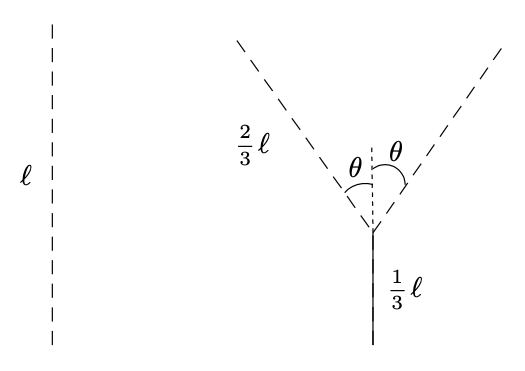> Base de la construction d'un arbre.

Les portions dessinées en pointillées sont celles sur lesquelles on appliquera la transformation à l’ordre suivant (on les appelle les segments non-terminaux). Les portions dessinées en trait plein sont des segments qui ne seront pas transformés (on les appellera les segments terminaux).

Pour transformer un segment non-terminal de longueur $l$, on trace un segment terminal de longueur $l/3$, puis deux segments non-terminaux de longueur $2l/3$ à un angle $\theta$ du premier segment.

Travail

Suivre la même démarche que pour le flocon de Koch pour écrire une fonction de signature qui trace l’arbre, et repositionne la tortue à son point de départ.

  • Dans un premier temps, gérer les ordres 0 et 1 (utiliser la méthode et aucun appel récursif), et tester la fonction. Vérifier en particulier que la tortue est bien revenue à son point de départ à la fin de l’exécution de la fonction dans les deux cas (n = 0 et n = 1).

  • Pour chaque tracé de segment non-terminal, remplacer l’appel à la méthode par un appel récursif à la fonction , et vérifier le comportement de la fonction à différents ordres. Cette fois-ci, une profondeur 10 ou 11 donne un résultat assez joli.

Solution 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

"""
Programme qui dessine un arbre fractal.
"""
import turtle
import math as m

def arbre(t: turtle, n: int, longueur: int, theta: int) -> None:

    if n == 0:
        t.color("red")
        t.forward(longueur)
        t.backward(longueur)
        t.color("black")

    else:
        t.width(n)
        t.forward(longueur / 3)
        t.left(theta)
        arbre(t, n-1, longueur / 3 * 2, theta)
        t.right(2 * theta)
        arbre(t, n-1, longueur / 3 * 2, theta)
        t.left(theta)
        t.backward(longueur / 3)

def main():
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)
    t.setheading(90)

    longueur = 300
    theta = 35
    n = 11

    arbre(t, n, longueur, theta)
    # enregistrement de l'image
    ts = turtle.getscreen()
    ts.getcanvas().postscript(file='arbre.pdf')

    turtle.mainloop()

main()
Fractales  Récursivité  Turtle 

Voir également