Superposition

Livre scolaire

• 32, 34, 33 pages 509 et 510

Annale

• Autour du papillon

Ne pas traiter les première et deuxième partie (seulement la partie 3).

• D'où viennent les couleurs des ailes des papillons ?

Interférences

Par la suite, toutes les ondes étudiées seront sinusoïdales, de même fréquence $f$.

Un exemple de montage d’étude d’une figure d’interférence

Schéma de principe

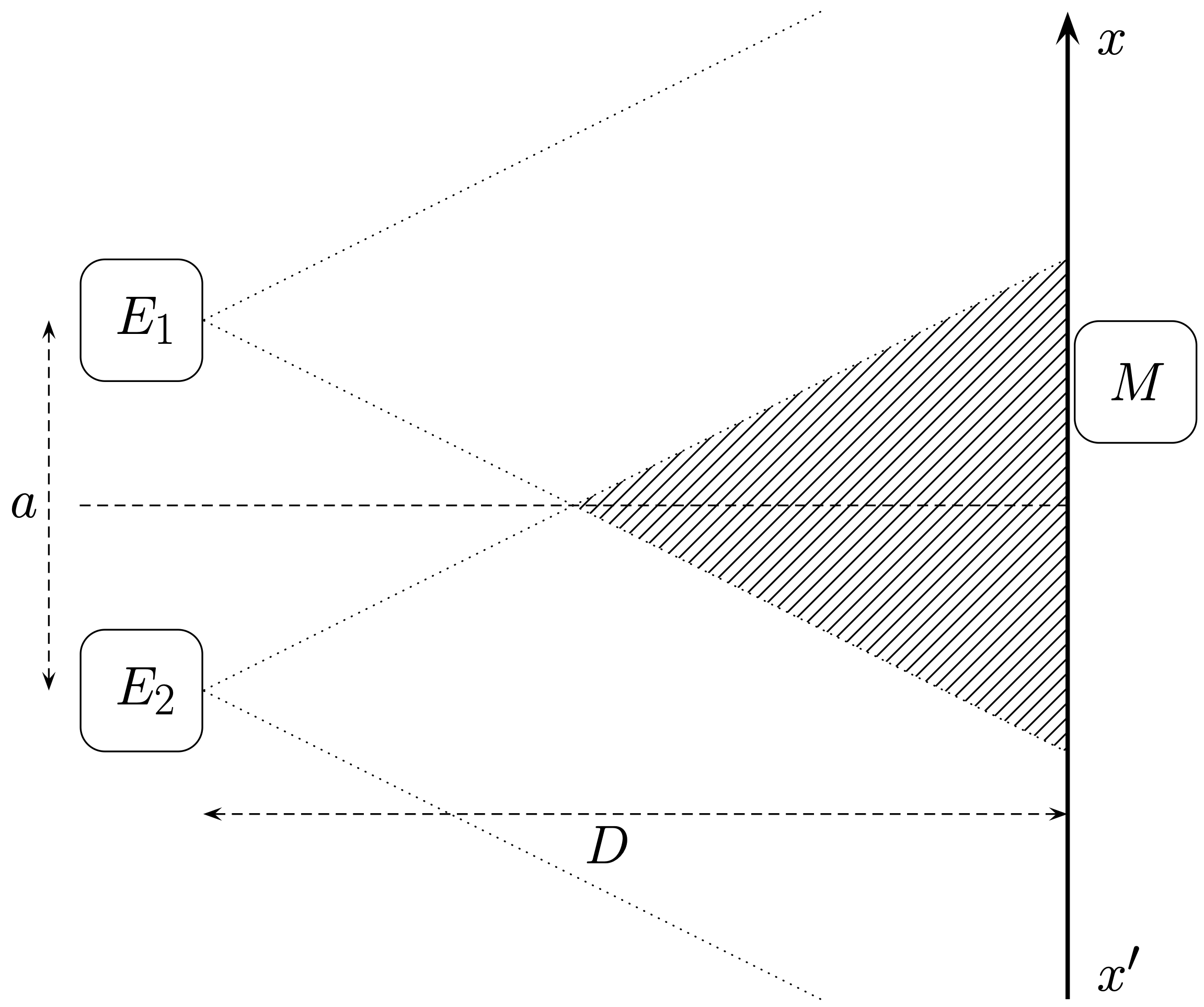
Deux ondes sinusoïdales de même fréquence $f$ sont émises par les deux émetteurs $E_1$ et $E_2$. L’émission de ces ondes s’effectuant dans un cône, ces ondes ne se superposent que dans la zone hachurée sur le schéma : c’est le champ d’interférence. Dans toute cette région, ces ondes interférent.

Émission de bips sonores par deux émétteurs

1. Deux émetteurs synchronisés, $E_1$ et $E_2$, émettent chacun un bip sonore, à la date $t=\pu{0 s}$ alors qu’un récepteur $R$ se trouve à la position $R_1$.
   Combien de bips perçoit le récepteur ? Pourquoi ?

Réponse

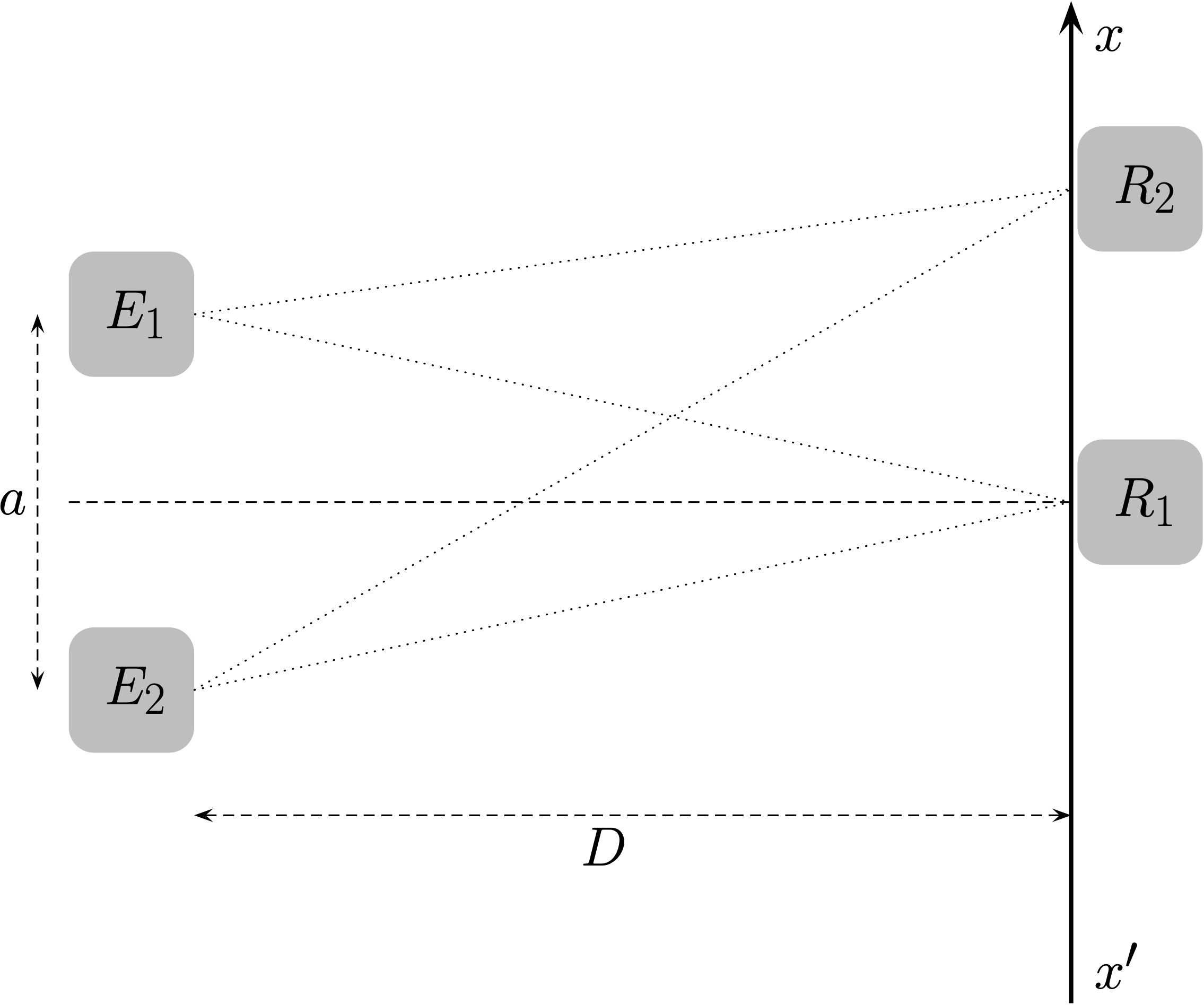
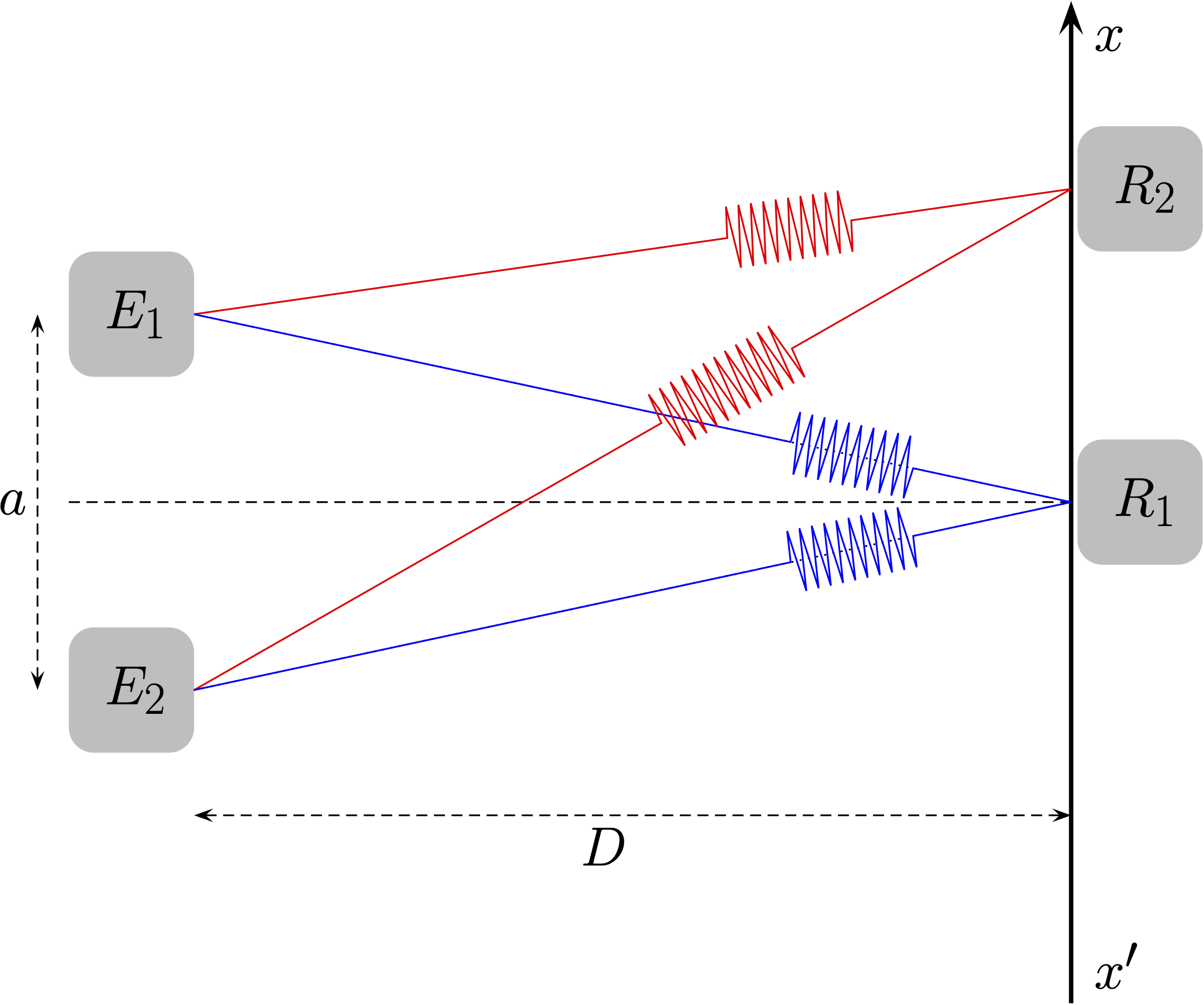Le récepteur perçoit un seul bip puisque les deux signaux doivent parcourir la même distance à la même vitesse (car ils se propagent dans le même milieu) et arrivent donc à la même date.

2. On place cette fois le récepteur à la position $R_2$. Que perçoit le récepteur dans ce cas ? Pourquoi ?

Réponse

Le signal issu de l'émetteur $E_1$ doit parcourir une plus petite distance que le signal issu de l'émetteur $E_2$ (ces signaux se propagent avec la même célérité puisqu'ils sont dans le même milieu). Le récepteur perçoit donc deux signaux : celui issu de $E_1$ puis celui issu de $E_2$.

3. Si on note $t_1$ la date à laquelle le récepteur positionné en $R_2$ reçoit le signal issu de $E_1$ et $t_2$ la date à laquelle ce même récepteur reçoit le signal issu de $E_2$, établir l’expression du retard $\tau$ avec lequel le deuxième signal arrive par rapport au premier.