Pression dans un fluide

Qu’est-ce que la pression ?

Regarder la vidéo suivante. Le narrateur explique le phénomène en utilisant le terme pression. Notre objectif est de parvenir à la même description mais sans utiliser le mot pression de façon à comprendre ce que ce concept signifie.
  1. Au niveau macroscopique, utiliser la notion de force pour décrire la déformation du ballon. Cette force porte le nom de force pressante.
Réponse

Au niveau macroscopique, un fluide exerce sur une paroi une force dirigée du gaz vers la paroi.

  1. Selon quelles directions s’exerce cette force ?
Réponse

La force pressante s’exerce selon une direction perpendiculaire à la surface.

  1. Au niveau microscopique, dire quelle est l’origine de la force pressante.
Réponse

Il est ici question de se demander quelle est l’origine physique de la force de pressante. Au niveau microscopique chaque millimètre-carré d’une paroi en contact avec un fluide subit des milliards de collisions chaque seconde. Lors de chacune de ces collisions les particules du fluide exercent une force sur cette paroi.

Synthèse
  • Un fluide exerce des forces pressantes, réparties sur la surface des objets avec lesquels il est en contact.
  • Un gaz exerce sur une petite portion de paroi une force pressante perpendiculaire à la surface, et dirigée du gaz vers la paroi.
  • Soit $F$ la valeur de la force pressante s’exerçant sur une surface plane d’aire $S$.
    Par définition, la pression du gaz est donnée par la relation : $$ p = \dfrac{F}{S} $$ avec $p$ en pascal (Pa), $F$ en newton (N) et $S$ en mètre-carré ($\pu{m2}$).
  • La pression d’un gaz se mesure avec un manomètre.

On emploie couramment d’autres unités de pression :

  • Le bar : $\pu{1 bar} = \pu{1e5 Pa}$ ;
  • L’hectopascal : $\pu{1 hPa} = \pu{1e2 Pa} = \pu{1 mbar}$ ;
  • L’atmosphère : $\pu{1 atm} = \pu{1,013e5 Pa}$.

Que représente la pression atmosphérique ?

Dire ce qu’est la pression atmosphérique et donner une image qui permet d’illustrer l’importance de la force qu’exerce l’atmosphère sur une surface de sol de $\pu{1 m2}$.
Synthèse
  • L’air exerce des forces pressantes sur toutes les surfaces avec lesquelles il est en contact. En tout point de l’atmosphère, il existe une pression exercée par l’air appelée pression atmosphérique. Elle est de l’ordre de $\pu{1 atm}$ (elle varie en fonction de la météorologie) au niveau de la mer et diminue avec l’altitude.
  • Les baromètres mesurent la pression atmosphérique.

Évolution de la pression en fonction de la profondeur pour un fluide incompressible : loi fondamentale de la statique des fluides

Détermination expérimentale

  • Réaliser le travail accessible à cette adresse.
Corrigé

Corrigé en ligne

Dans un fluide au repos, la pression $P$ n’est pas uniforme en tout point du fluide. La loi fondamentale de la statique des fluides permet de relier la variation de la pression d’un fluide à sa masse volumique $ρ$, au champ de pesanteur $g$ et à la profondeur $h$.

La masse volumique $rho$ d’un fluide est la masse de ce fluide par unité de volume : $$ \rho = \dfrac{m}{V} $$ $\rho$ s’exprime en kilogramme par mètre-cube ($\pu{kg.m-3}$).
Dans cette section, le fluide est considéré incompressible : sa masse volumique est une constante. Il ne peut donc pas s’agir d’un gaz.
Pour un fluide incompressible dans un champ de pesanteur uniforme, la loi fondamentale de la statique des fluides s’écrit : $$ P + \rho \, g\, z = \text{cste} $$ à la condition que l’axe $(Oz)$ soit orienté vers le haut.
Dans cette relation, $\rho$ en kilogramme par mètre-cube ($\pu{kg.m-3}$), $P$ en pascal (Pa) et $z$ en mètre.

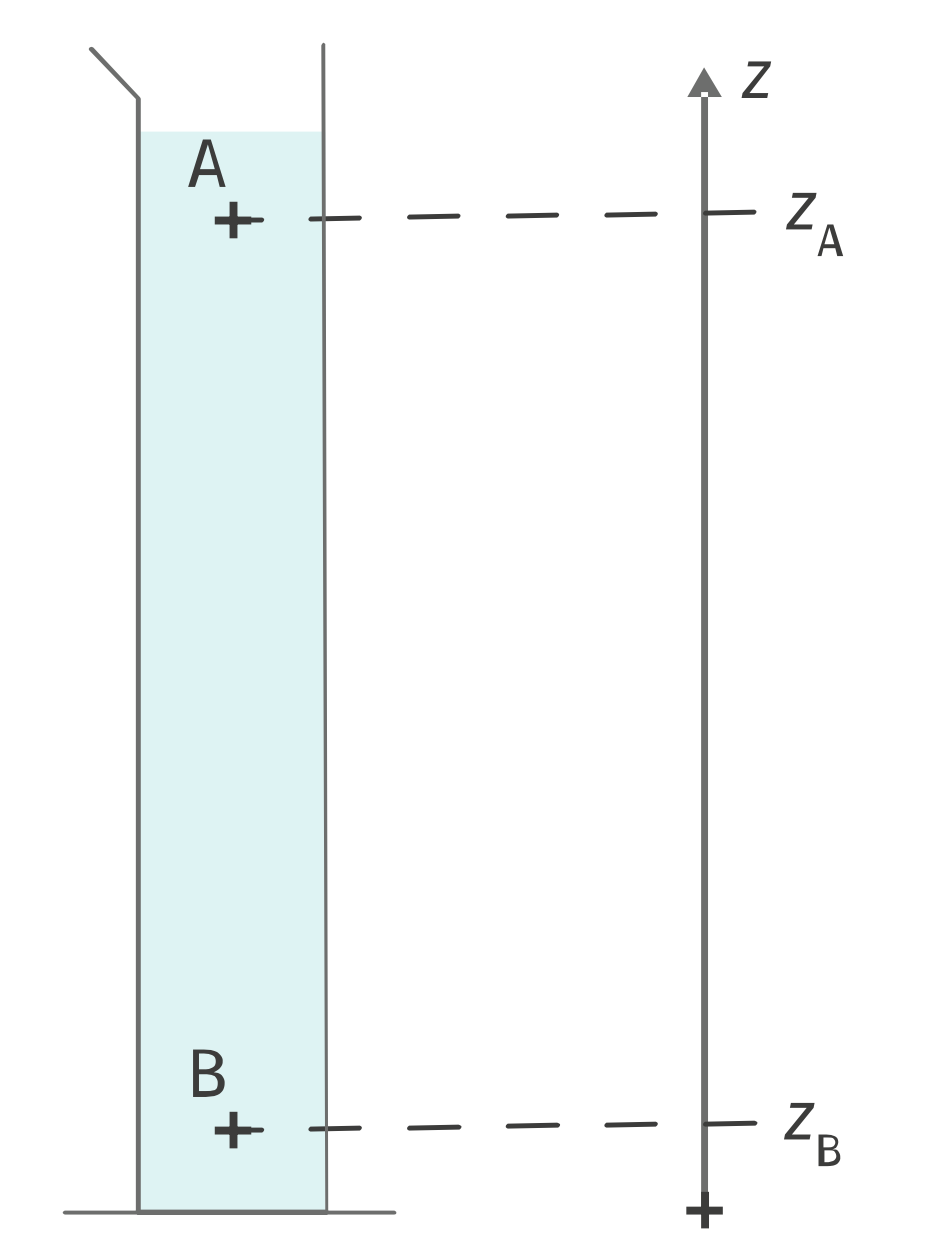
Quelle est la relation entre $P_A$ et $P_B$ ?

Réponse

$$ P_A + \rho \, g\, z_A = P_B + \rho \, g\, z_B $$

$$ P_B = P_A + \rho \, g\, (z_A - z_B) $$

Application : le tonneau de Pascal