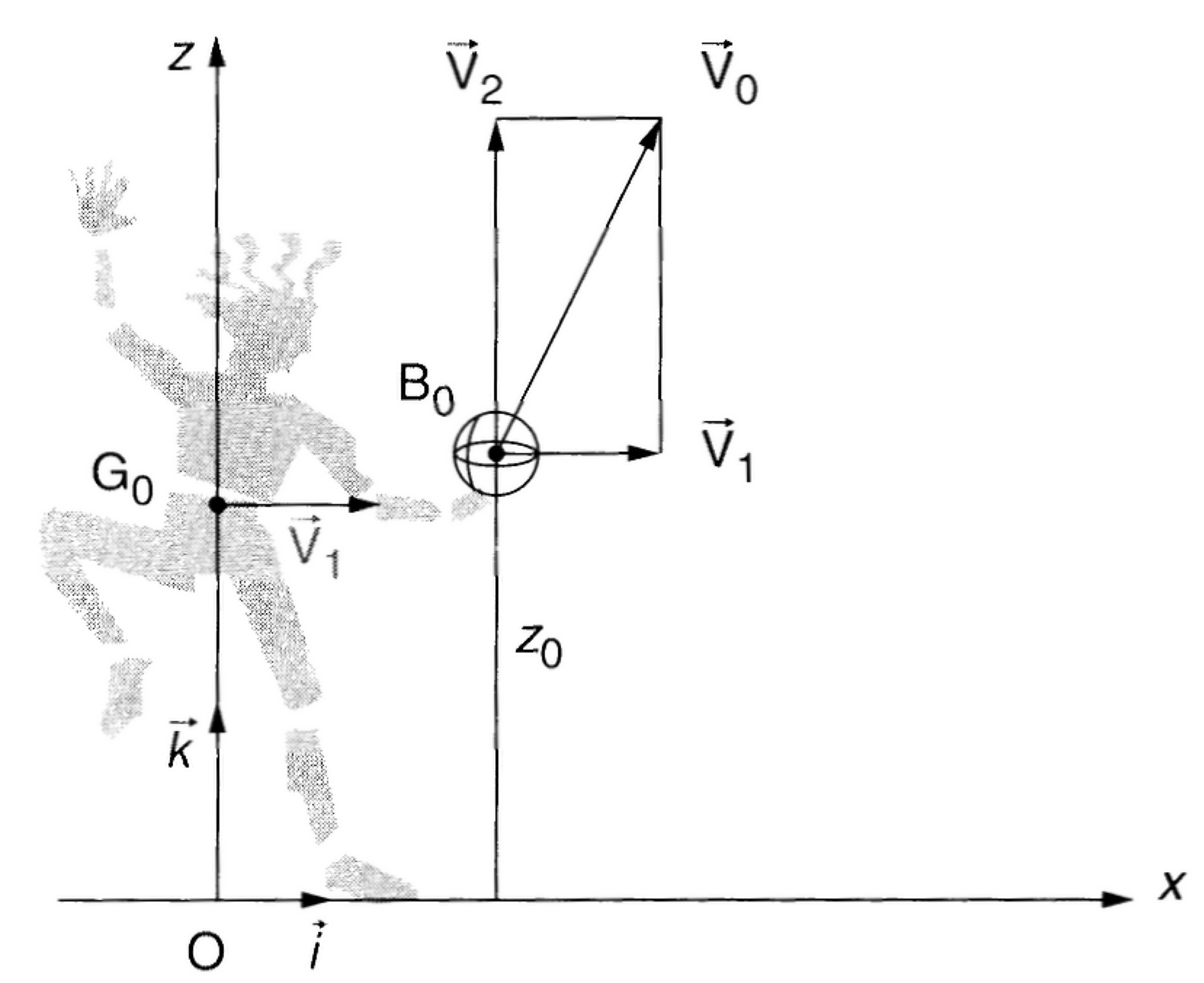
Cet exercice a pour objet l’étude du mouvement d’une gymnaste de GRS. Dans un référentiel lié à la salle de gymnastique, la gymnaste est en mouvement rectiligne uniforme à la vitesse $\overrightarrow{V_1}$. Dans ce même référentiel, à l’instant du lancer, la vitesse du ballon est $\overrightarrow{V_0}$. Cette vitesse possède, par rapport aux axes de projection, une composante horizontale $V_{0x}$ égale à $V_1$ et une composante verticale $V_{0z}$ notée $V_2$.
L’instant du lancer est choisi comme origine des dates $t = \pu{0 s}$. Dans le référentiel de la salle, on considère le repère $(O; \vec{i}, \vec{j}, \vec{k})$ défini de la manière suivante : l’origine $O$ correspond à la projection du centre d’inertie $G_0$ de la gymnaste sur le sol horizontal à l’instant du lancer ; l’axe $(Ox)$ est horizontal et l’axe $(Oz)$ vertical ascendant. Le centre $B$ du ballon se trouve au point $B_0$ de coordonnées $(x_0, y_0)$ à l’instant du lancer.
Dans la salle, le champ de pesanteur est uniforme et noté $\vec{g}$. Dans tout le problème, on néglige l’action de l’air.
Aucune application numérique n’est demandée !
Toutes les réponses sont à exprimer en fonction des données : $g$, $V_1$, $V_2$, $x_0$ et $z_0$.
Mouvement de la gymnaste
- À partir de la description du mouvement de la gymnaste faite dans l’énoncé, écrire la deuxième loi de Newton décrivant ce mouvement. On notera $\overrightarrow{a_G}$ l’accélération de la gymnaste. Justifier la réponse.
Réponse
Le mouvement de la gymnaste est rectiligne et uniforme ; son accélération est donc nulle $$\overrightarrow{a_G} = \vec{0}$$
- En déduire les expressions $V_{x_G} (t)$ et $V_{z_G} (t)$ des composantes du vecteur vitesse de la gymnaste.
Réponse
On projette la deuxième loi de Newton dans le repère $(O; \vec{i}, \vec{k})$ : $$ \begin{cases} a_{x_G} = 0 = \dfrac{\mathrm{d}V_{x_G}}{\mathrm{dt}} & \implies V_{x_G} (t) = A \\ & \\ a_{z_G} = 0 = \dfrac{\mathrm{d}V_{z_G}}{\mathrm{dt}} & \implies V_{z_G} (t) = B \\ \end{cases} $$ Les conditions initiales pour la gymnaste ne sont pas explicitement données mais on sait qu’à chaque instant $$ \begin{cases} V_{x_G}(t) = V_1 & \implies V_{x_G}(0) = V_1 = A \\ & \\ V_{z_G} (t) = 0 & \implies V_{Z_G}(0) = 0 = B\\ \end{cases} $$ On en conclut donc que $$ \begin{cases} V_{x_G}(t) = V_1 & \\ & \\ V_{z_G} (t) = 0 & \\ \end{cases} $$
- Déterminer les équations horaires $x_G (t)$ et $z_G (t)$ du mouvement du centre d’inertie $G$ de la gymnaste par rapport au référentiel lié à la salle.
Réponse
$$ \begin{cases} V_{x_G} = V_1 = \dfrac{\mathrm{d} x_G}{\mathrm{dt}} & \implies x_G (t) = V_1 t + C \\ & \\ V_{z_G} = 0 = \dfrac{\mathrm{d} z_G}{\mathrm{dt}} & \implies z_G (t) = D \\ \end{cases} $$ On considère que la gymnaste se trouve à l’origine du repère à la date $t=0$. On a donc $$ \begin{cases} x_G(0) = V_1 \times 0 + C = 0 & \implies C = 0 \\ & \\ z_G (0) = D = z_{G0} & \implies D = z_{G0}\\ \end{cases} $$ Finalement $$ \begin{cases} x_G(t) = V_1 t & \\ & \\ z_G (t) = z_{G0} & \\ \end{cases} $$
Mouvement du ballon
- À partir des informations données dans l’énoncé indiquer comment la gymnaste lance le ballon, par rapport à un référentiel qui lui serait lié. La réponse à cette question n’est pas indispensable à la poursuite de cet exercice.
Réponse
Grâce au schéma donné, on constate que la vitesse initiale $\overrightarrow{V_0}$ que la gymnaste communique au ballon possède une composante horizontale $\overrightarrow{V_1}$, identique à la vitesse de la gymnaste. On peut donc en déduire que la gymnaste lance le ballon verticalement vers le haut (par rapport à elle-même).
- Écrire la deuxième loi de Newton pour le mouvement du ballon. On notera $\overrightarrow{a_B}$ l’accélération du ballon.
Comment peut-on qualifier le mouvement du ballon ?
Réponse
- Système = {ballon}
- Référentiel = {terrestre considéré galiléen}
- Interactions :
- Système - air : négligée ;
- Sytème - champ de pesanteur modélisée par le poids $\overrightarrow{P} = m \vec{g}$.
- Deuxième loi de Newton : $m \overrightarrow{a_G} = m \vec{g} \iff \overrightarrow{a_G} = \vec{g}$
Le ballon est en chute libre.
- En déduire les expressions $V_{x_B} (t)$ et $V_{z_B} (t)$ des composantes du vecteur vitesse du ballon.
Réponse
On projette la deuxième loi de Newton dans le repère $(O; \vec{i}, \vec{k})$ : $$ \begin{cases} a_{x_B} = 0 = \dfrac{\mathrm{d}V_{x_B}}{\mathrm{dt}} & \implies V_{x_B} (t) = E \\ & \\ a_{z_G} = -g = \dfrac{\mathrm{d}V_{z_B}}{\mathrm{dt}} & \implies V_{z_B} (t) = -gt + F \\ \end{cases} $$ Conditions initiales : $$ \begin{cases} V_{x_B}(0) = E = V_1 & \implies E = V_1 \\ & \\ V_{z_B}(0) = -g \times 0 + F = V_2 & \implies F = V_2\\ \end{cases} $$ Finalement $$ \begin{cases} V_{x_B} (t) = V_1 t & \\ & \\ V_{z_B} (t) = -gt + V_2 & \\ \end{cases} $$
- En déduire les équations horaires $x_B (t)$ et $z_B (t)$ du ballon.
Réponse
$$ \begin{cases} V_{x_B} (t) = V_1 = \dfrac{\mathrm{d}x_B}{\mathrm{dt}} & \implies x_B (t) = V_1 t + G \\ & \\ V_{z_B} = -gt + V_2 = \dfrac{\mathrm{d}z_B}{\mathrm{dt}} & \implies z_B (t) = -\dfrac{1}{2}gt^2 + V_2 t + H \\ \end{cases} $$ Conditions initiales : $$ \begin{cases} x_B(0) = V_1 \times 0 + G = x_0 & \implies G = x_0 \\ & \\ z_B(0) = -\dfrac{1}{2}g \times 0^2 + V_2 \times 0 + H = z_0 & \implies H = z_0\\ \end{cases} $$ Finalement $$ \begin{cases} x_B (t) = V_1 t + x_0 & \\ & \\ z_B (t) = -\dfrac{1}{2}gt^2 + V_2 t + z_0 & \\ \end{cases} $$
- Déterminer l’équation de la trajectoire du point $B$ et tracer, à la main, l’allure de la courbe correspondante sur votre feuille, en y faisant apparaître le vecteur $\overrightarrow{V_0}$.
Réponse
Pour déterminer l’équation de la trajectoire il faut éliminer le temps des équations horaires.
Comme $$t = \dfrac{x_B - x_0}{V_1}$$ l’équation est
$$
z_B = -\dfrac{1}{2}g\left( \dfrac{x_B - x_0}{V_1} \right)^2 + V_2 \left( \dfrac{x_B - x_0}{V_1} \right)+z_0
$$
- Quelles sont les caractéristiques du vecteur vitesse du point $B$ au sommet de sa trajectoire ? Quelle est la hauteur maximale atteinte par le point $B$ ?
Réponse
Au sommet de la trajectoire, la composante verticale de la vitesse s’annule. Le vecteur vitesse est alors horizontal.
Soit $t_S$ la date à laquelle le ballon atteint le sommet de la trajectoire. $t_S$ est donc telle que $$V_{x_B}(t_S) = 0$$ On a donc $$ 0 = -gt_S + V_2 \iff t_S = \dfrac{V_2}{g} $$ Si on injecte l’expression de $t_S$ dans l’équation horaire qui donne l’altitude du ballon, on obtient $$ z_B(t_S) = -\dfrac{1}{2}gt_S^2 + V_2 t_S + z_0 \iff z_B(t_S) = \dfrac{1}{2}\dfrac{V_2^2}{g} + z_0 $$
Rattraper du ballon par la gymnaste
- La gymnaste récupère le ballon lorsque son centre $B$ repasse à l’altitude $z_0$. Déterminer le temps de vol $t_V$ du ballon.
Comment la gymnaste peut-elle augmenter cette durée ?
Réponse
La date $t_V$ est telle que $z_B(t_V) = z_0$. On a donc $$ -\dfrac{1}{2}gt_V^2 + V_2 t_V + z_0 = z_0 \iff t_V \left( -\dfrac{1}{2}gt_V + V_2 \right) = 0 $$ L’équation admet deux solutions $$ \begin{cases} t_V = 0 & \text{C’est l’instant du lancer} \\ t_V = \dfrac{2V_2}{g} & \text{C’est la date recherchée} \\ \end{cases} $$ La gymnaste peut augmenter le temps de vol en lançant le ballon vers le haut avec une vitesse initiale $V_2$ plus grande.
- Déterminer la distance parcourue par le centre d’inertie $B$ du ballon suivant l’axe horizontal $(Ox)$ pendant le temps de vol.
De quel(s) paramètre(s) dépend cette distance ?
Réponse
À la date $t_V$ le ballon se trouve à l’abscisse $x_B(t_V)$ dont l’expression est : $$ x_B(t_V) = \dfrac{2V_1V_2}{g} + x_0 $$ Comme l’abscisse à laquelle se trouve le ballon à la date $t=0$ est $x_0$, la distance parcourue horizontalement pendant la durée $t_V$ est $$ x_B(t_V) - x_B(0) = \dfrac{2V_1V_2}{g} +x_0 - x_0 = \dfrac{2V_1V_2}{g} $$ On constate que la distance parcourue horizontalement pendant la durée $t_V$ dépend des deux composantes de la vitesse initiale communiquée par la gymnaste :
- plus elle va vite plus la distance parcourue est grande ;
- plus elle lance le ballon avec une vitesse verticale élevée, plus la distance parcourue est grande.
- Montrer que la distance parcourue par le centre d’inertie $G$ de la gymnaste pendant ce temps de vol est identique et qu’elle a donc de grandes chances de rattraper le ballon.
Réponse
On cherche à déterminer la distance parcourue par la gymnaste pendant le temps de vol du ballon.
À la date $t_V$, l’abscisse à laquelle se trouve la gymnaste est
$$
x_G (t_V) = V_1 t_V = \dfrac{2V_1V_2}{g}
$$
Elle parcourt donc la distance
$$
x_G (t_V) - x_G (0) = \dfrac{2V_1V_2}{g}
$$
La gymnaste parcourt la même distance que le ballon horizontalement. Elle a donc de fortes chances de le rattraper.