Chute libre verticale dans le champ de pesanteur uniforme, quelques tracés de courbes à l'aide de Python

L’objectif de ce document est de tracer les équations horaire ainsi que les expressions des différentes formes d’énergies à l’aide du langage de programmation Python. Il n’est pas question ici de redémontrer toutes les formules mais je vous encourage à le faire.

Les codes Python proposés sont loin d’être optimaux, mon objectif est que vous soyez capables de les comprendre. En fait, on réalise plusieurs fois les mêmes actions tout au long de cette activité ; il ne faut donc pas se laisser impressionner par la longueur du code.

Situation étudiée

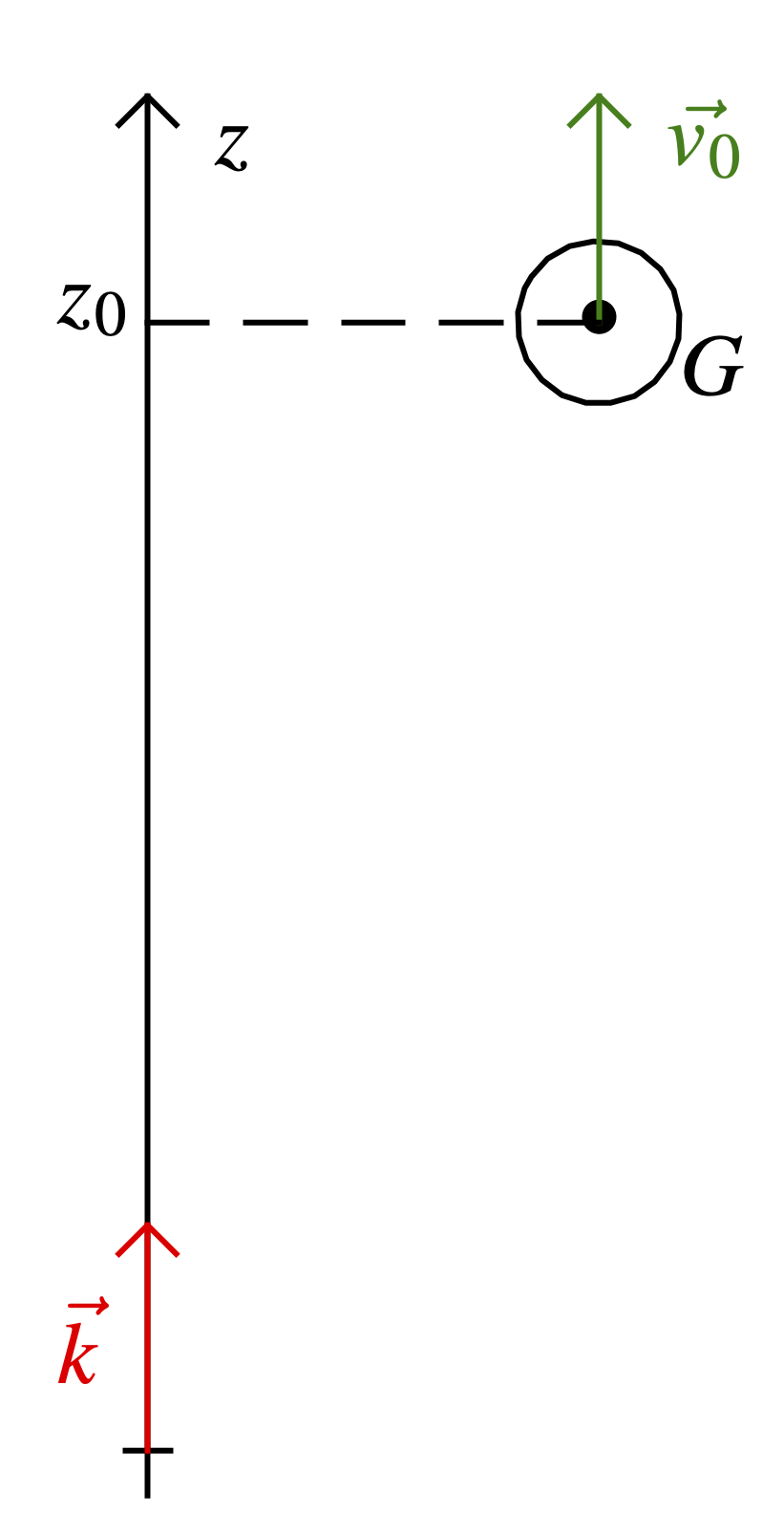
On lance une balle, de masse $m$, verticalement vers le haut depuis l’altitude $z_{0}$ au dessus de l’origine choisie.

On a démontré dans ce document que les équations horaires du mouvement ont pour expression : $$ \begin{aligned} a_z(t) &= -g\\ v_z(t) &= -g t + v_0\\ z(t) &= -\dfrac{1}{2}\, gt^2 + v_0t + h_0 \end{aligned} $$ et que les différentes formes d’énergies ont pour expression : $$ \begin{aligned} E_C &= \dfrac{1}{2}\, mv^2\\ E_{PP} &= mgz\\ E_M &= E_C + E_{PP} \end{aligned} $$

Remarque 1
L’expression de l’énergie potentielle de pesanteur suppose ici que $E_{PP}(0) = 0$ (l’énergie potentielle de pesanteur est nulle lorsque la variable $z$ est nulle).
Remarque 2
Le système étant en chute libre, l’interaction avec l’air est négligée et l’énergie mécanique se conserve.

Travail à réaliser

Un corrigé de cette activité se trouve à cette adresse. Essayez de répondre aux différentes questions avant de le consulter.

Remarque
Pour accéder au code, cliquez sur le bouton Show files.
Le programme réalise plusieurs tracés successivement. Il faut donc fermer chaque fenêtre qui affiche un tracé, en cliquant sur la croix en haut à droite de la fenêtre, pour pouvoir faire apparaître le suivant.

  1. Le fichier de travail se trouve à cette adresse. Cliquez sur le bouton Fork repl afin de copier la structure du code dans votre profil personnel sur Replit.com. Il vous sera demandé de vous connecter si vous ne l’avez pas fait au préalable.

  2. Dans la partie # Définition des paramètres du problème affecter les valeurs numérique suivantes aux différentes variables, ligne 154 et suivantes, sachant que $g= \pu{9.8 m.s-2}$, $v_0 = \pu{10 m.s-1}$ (vers le haut), $h_0 = \pu{15 m}$, $t_0 = \pu{0 s}$ (première date), $t_{max} = \pu{3 s}$ (dernière date), $dt = \pu{0.01 s}$ (écart entre deux dates successives), $m = \pu{0,2 kg}$ (masse de la balle).

Solution 
1
2
3
4
5
6
7

g = 9.8  # m.s^{-2}
v0 = 10  # m.s^{-1}
h0 = 15  # m
t0 = 0  # s
tmax = 3  # s
dt = 0.01  # s
m = 0.2  # kg
  1. La fonction creation_liste_des_dates crée la liste des dates auxquelles seront calculées les grandeurs physiques. La première date est t0, la dernière est inférieure ou égale à tmax et le pas entre deux dates est dt. Compléter les lignes de codes à partir de la ligne 52 qui permettent de construire cette liste.
Solution 
1
2
3
4
5
6

dates = []  # Création d'une liste vide

t = t0  # Initialisation du compteur
while t <= tmax:  # Tant que t <= tmax Faire
    dates.append(t)  # Ajout de t à la fin de la liste
    t = t + dt  # Incrémentation du compteur
  1. La fonction creation_liste_az crée la liste des valeurs de la composante $a_z$ de l’accélération $\vec{a}$ sur l’axe $(Oz)$ aux différentes dates.
Python 

Suggestions de lecture :