Les lois de Newton seules sont insuffisantes pour décrire l’équilibre des systèmes dans le cas général. Leur utilisation conduit cependant à la solution des problèmes dans les deux cas suivants :
- Le système est soumis à deux forces ayant même droite d’action ;
- Le système est soumis à plusieurs forces coplanaires et concourantes.
Exercice 1
- Un ressort, dont l’une des extrémités est liée à un point fixe, s’allonge proportionnellement à l’intensité de la force appliquée à son autre extrémité.
- $$F = k \cdot \Delta l$$
- où $\Delta l$ est l’allongement du ressort.
- Remarque.
- $k$, le coefficient de proportionnalité, est appelé constante de raideur du ressort ; son unité est le newton par mètre.
Appliquons cette caractéristique dans le cas particulier suivant : une masse $m = \pu{2 kg}$ est fixée à l’extrémité d’un ressort accroché au plafond. Quel est l’allongement de ce ressort ?
- Données :
- $k = \pu{1000 N.m-1}$ et $g = \pu{10 N.kg-1}$.
Solution
Exercice 2
- Théorème d’Archimède :
- Un corps immergé dans un fluide est soumis, de la part de ce fluide, à des actions équivalant à une force unique dirigée de bas en haut, égale au poids du fluide déplacé et appliquée au centre d’inertie du fluide déplacé.
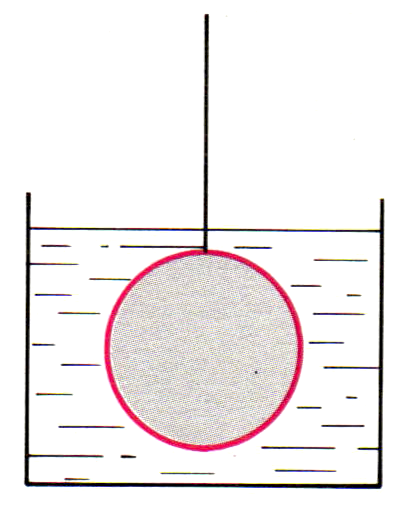
Appliquons ce théorème dans le cas particulier suivant (figure ci-dessous) : Une boule, de rayon $R=\pu{10 cm}$ et de masse $m = \pu{10 kg}$, est immergée dans l’eau. Elle est retenue par un fil relié à un dynamomètre. Quelle est l’indication du dynamomètre ?
- Données :
- $g = \pu{10 N.kg-1}$ ; masse volumique de l’eau $\rho = \pu{1,0e3 kg.m-3}$.
Solution
Exercice 3
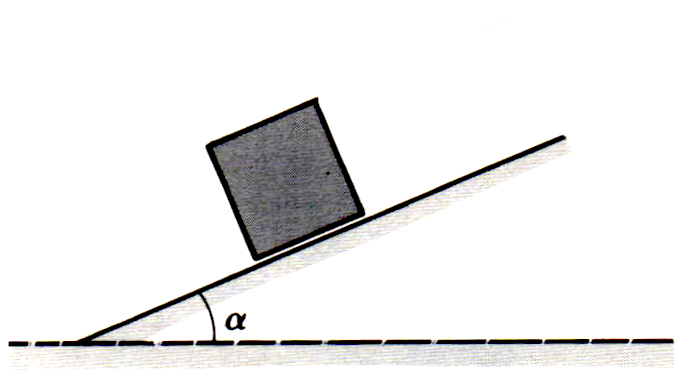
Un solide de masse $m=\pu{2 kg}$ est posé sur un plan incliné d’un angle $\alpha = 30 \text{°}$ par rapport à l’horizontale. Ce solide est immobile grâce aux forces de frottement solide. Calculer la valeur $f$ de la force de frottement solide.
- Donnée :
- $g = \pu{10 N.kg-1}$
Solution
Exercice 4
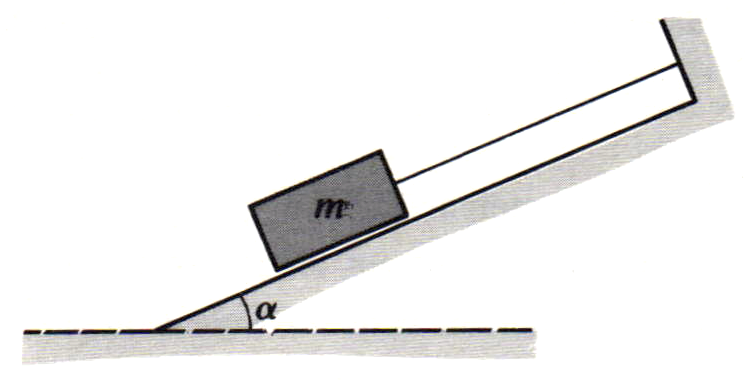
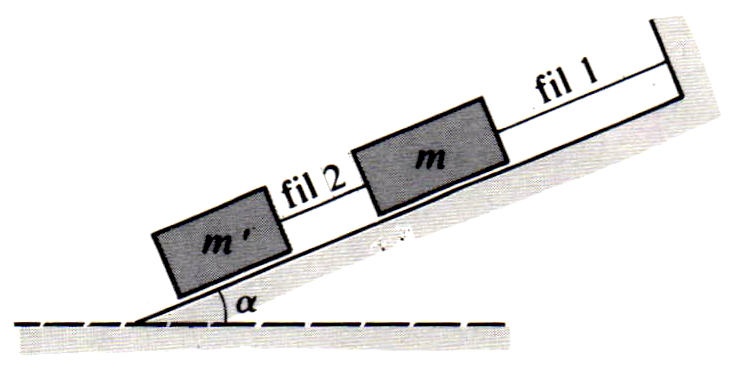
Un solide de masse $m = \pu{2 kg}$ peut glisser sans frottement le long de la plus grande pente d’un plan incliné faisant un angle $\alpha = 30 \text{°}$ avec l’horizontale. Ce solide est retenu par un fil de masse négligeable, parallèle au plan comme l’indique la figure ci-dessous. Déterminer :
- La valeur de la tension $T$ du fil.
- La valeur de la réaction du plan.
- Donnée :
- $g = \pu{10 N.kg-1}$
- À ce solide est accroché par un fil 2, et dans les mêmes conditions qu’à la question précédente, un deuxième solide, de masse $m’ = \pu{1 kg}$, comme l’indique la figure ci-dessous. Déterminer la tension de chacun des deux fils.
Solution
Exercice 5
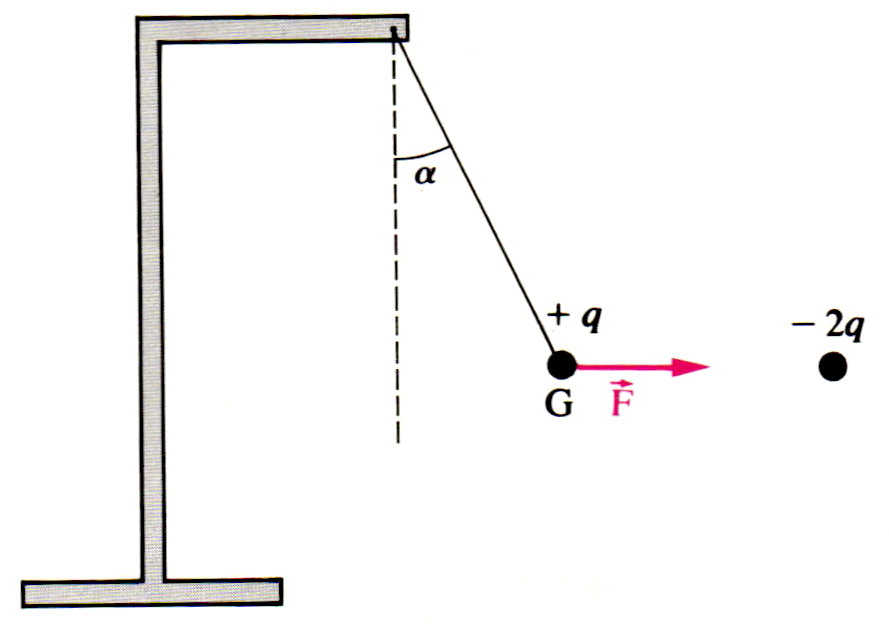
La boule d’un pendule électrostatique, de poids $\pu{0,02 N}$ portant une charge $+q$ est attirée par une charge électrique $-2q$. Les forces électriques exercées sur la boule sont équivalentes à une force horizontale, $\overrightarrow{F}$, de droite d’action passant par $G$ (centre d’inertie de la boule) et de norme $\pu{0,02 N}$. Déterminer :
- L’angle $\alpha$ que fait le fil avec la verticale.
- La force électrique exercée par la charge $+q$ sur la charge $-2q$ et la tension $\overrightarrow{T}$ du fil.
Solution
Exercice 6
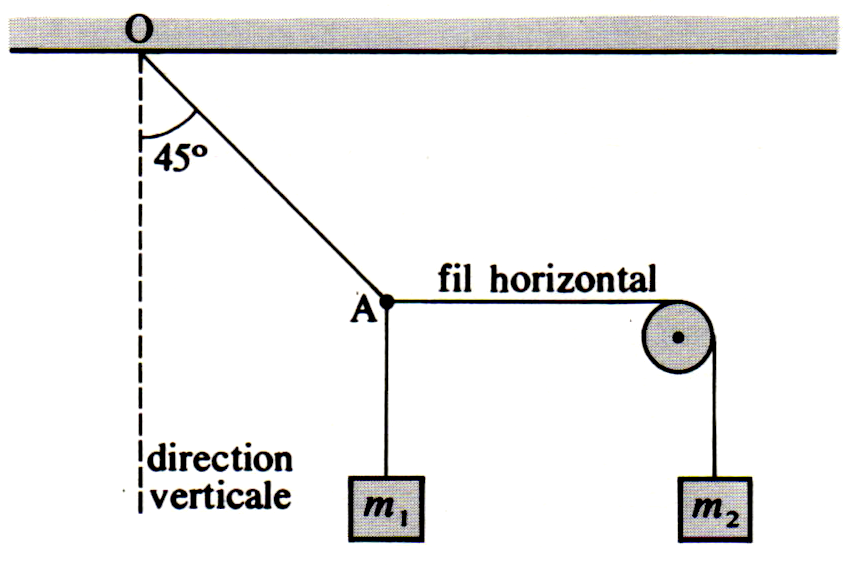
À l’équilibre, le fil inextensible (de masse négligeable) $OA$ (figure ci-dessous) fait un angle de 45° avec la verticale.
- Calculer la tension du fil $OA$.
- Calculer la valeur de la masse $m_2$ nécessaire pour réaliser cet équilibre.
- Cet équilibre dépend-il de la valeur de $g$ ?
- Données :
- Poids de $m_1$ : $\pu{4 N}$ ; $g = \pu{10 N.kg-1}$.
Solution
Exercice 7
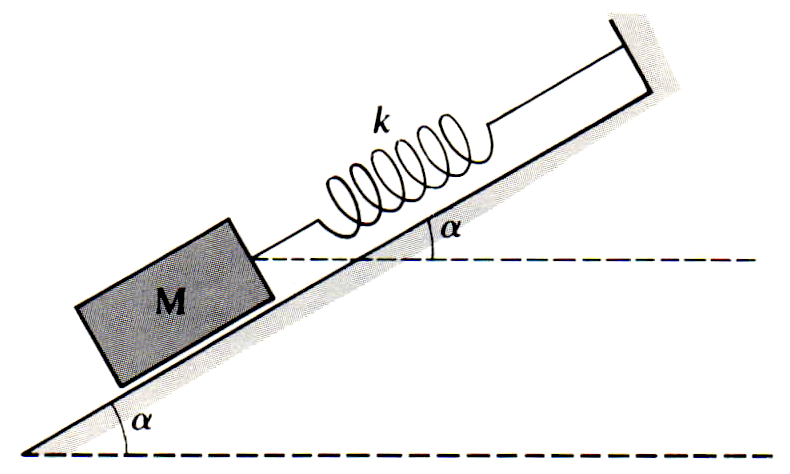
Un corps $M$, de masse $m=\pu{10 kg}$, est posé sur un plan incliné faisant un angle $\alpha$ avec l’horizontale. Ce corps est retenu, comme l’indique la figure ci-dessous, par un ressort de raideur $k = \pu{1000 N.m-1}$.
- Tracer le graphique de la fonction qui associe l’allongement du ressort au sinus de l’angle $\alpha$. On prendra $g = \pu{10 N.kg-1}$, et on ne tiendra pas compte des frottements.
- En déduire la valeur de l’allongement pour $\alpha = 30\text{°}$, puis $\alpha = 60\text{°}$.
- Si l’allongement est de $\pu{7 cm}$, que vaut $\alpha$ ?