La neige tombe, les mains commencent à s’engourdir et le refuge est encore loin. Le randonneur sort alors de son sac à dos une pochette en plastique, remplie d’un liquide transparent et appuie sur un petit disque métallique placé à l’intérieur : le liquide commence à se solidifier tout en dégageant une douce chaleur.
Ce dispositif nommé chaufferette chimique est constitué d’une enveloppe souple de plastique qui contient une solution aqueuse d’acétate de sodium à 20 % en masse minimum. La solidification s’amorce à partir du disque, localement la solution s’échauffe. L’énergie qu’il a fallu fournir au matériau pour le faire fondre est restituée […]. Après utilisation, on peut régénérer la chaufferette en faisant fondre le solide obtenu par chauffage. On laisse alors le matériau doucement refroidir…
Pour la Science (2008)
Après l’étude d’une solution d’éthanoate de sodium (ou acétate de sodium), on se propose de vérifier par un titrage pH-métrique que la solution contenue dans une chaufferette chimique est une solution saturée en éthanoate de sodium.
Données 
- Produit ionique de l’eau : $K_e = \dfrac{[\ce{H3O^+}] \cdot [\ce{HO^-}]}{C_0^2} = \pu{1,0e-14}$ à $\pu{25 °C}$ ;
- Constante apparaissant dans l’expression du pH et du produit ionique de l’eau : $C_0 = \pu{1,0 mol.L-1}$ ;
- Masse molaire de l’éthanoate de sodium : $M(\ce{CH3COONa}) = \pu{82,0 g.mol-1}$ ;
- La solubilité notée s d’une espèce chimique exprimée en $\pu{g.L-1}$ est la masse maximale de cette espèce que l’on peut dissoudre dans un litre de solution à une température donnée ;
- Solubilité de l’éthanoate de sodium dans l’eau à $\pu{25 °C}$ : $s = \pu{365 g.L-1}$ soit $\pu{4,5 mol.L-1}$.
Étude d’une solution aqueuse d’éthanoate de sodium
L’éthanoate de sodium $\ce{CH3COONa}$ est un solide blanc. En solution aqueuse, l’éthanoate de sodium se dissocie $$\ce{CH3COONa(s) ->[eau] CH3COO^-(aq) + Na^+(aq) }$$
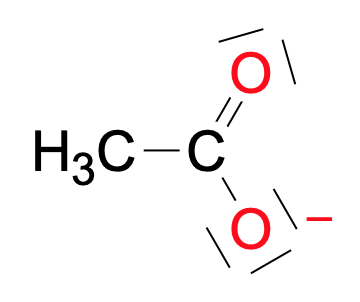
- Justifier, en s’appuyant sur la représentation de Lewis de l’ion, que l’ion éthanoate est une base selon Brönsted. En déduire le couple acido-basique correspondant.
Réponse
-
L’ion comporte un atome d’oxygène porteur d’une charge négative et de doublets non liants. Cette zone est donc un site riche en électrons, capable de réagir avec des atomes d’hydrogène déficitaires en électrons car liés à des atomes plus électronégatifs, dans une autre entité. C’est le comportement d’une base selon Brönsted.
-
Couple : $\ce{CH3COOH/CH3COO^-}$.
- Écrire l’équation de la réaction chimique entre l’ion éthanoate $\ce{CH3COO^-(aq)}$ et l’eau.
Réponse
$$\ce{CH3COO^-(aq) + H2O <=> CH3COOH + HO^- }$$
Lorsqu’on introduit dans un bécher un volume $V = \pu{100 mL}$ d’une solution $S$ d’éthanoate de sodium dont la quantité de matière en soluté apporté est $n = \pu{1,0e-2 mol}$, le pH mesuré de cette solution $S$ est égal à $\pu{8,9}$.
- Construire le tableau d’avancement de cette réaction en utilisant la quantité de matière $n$ et l’avancement $x$ de la réaction.
Réponse
| État | Av. | $\ce{CH3COO^-(aq)}$ | $\ce{H2O}$ | $\ce{CH3COOH}$ | $\ce{HO^-}$ |
|---|---|---|---|---|---|
| Initial | 0 | $n$ | excès | 0 | 0 |
| Interm. | $x$ | $n-x$ | excès | $x$ | $x$ |
| Final | $x_f$ | $n-x_f$ | excès | $x_f$ | $x_f$ |
| Final hypothétique | $x_{max}$ | $n-x_{max}$ | excès | $x_{max}$ | $x_{max}$ |
- Calculer la concentration $[\ce{H3O^+}]$ en ions oxonium $\ce{H3O^+}$ à l’équilibre dans la solution.
En déduire la valeur de la concentration en ions hydroxyde à l’équilibre $[\ce{HO^-}]$, à la température de $\pu{25 °C}$.
Réponse
-
$pH = -\log \left( \dfrac{[\ce{H3O^+}]}{C_0} \right) \Harr \boxed{[\ce{H3O^+}] = C_0 \cdot 10^{- pH}}$.
-
A.N. $[\ce{H3O^+}] = \pu{1,0 mol.L-1} \cdot 10^{- 8,9} = \pu{1,3e-9 mol.L-1}$.
-
$K_e = \dfrac{[\ce{H3O^+}] \cdot [\ce{HO^-}]}{C_0^2} \Harr \boxed{[\ce{HO^-}] = \dfrac{K_e \cdot C_0^2}{ [\ce{H3O^+}] }}$.
-
A.N. $[\ce{HO^-}] = \dfrac{\pu{1,0e-14} \times (\pu{1,0 mol.L-1})^2}{ \pu{1,3e-9 mol.L-1} } = \pu{7,9e-6 mol.L-1}$
- Pour la solution préparée, calculer l’avancement à l’équilibre $x_{eq}$.
Réponse
-
Le tableau d’avancement nous apprend que $[\ce{HO^-}] = \dfrac{x_f}{V} \leftrightarrow \boxed{ x_f = [\ce{HO^-}] \cdot V}$.
-
A.N. $ x_f = \pu{7,9e-6 mol.L-1} \times \pu{100e-3 L} = \pu{7,9e-7 mol.L-1}$.
- La transformation chimique est-elle totale ?
Réponse
-
À partir de la définition de l’avancement maximal $x_{max}$ et du tableau d’avancement, on peut écrire que $n - x_{max} = 0 \Leftrightarrow \boxed{ x_{max} = n }$.
-
A.N. $x_{max} = \pu{1,0e-2 mol}$.
-
$x_{max} \ggg x_f$, le système n’avance quasiment pas. La quantité de produits fabriqués est très petite.
Titrage de la solution d’éthanoate de sodium contenue dans une chaufferette chimique
Une chaufferette chimique contient une solution aqueuse $S_0$ d’éthanoate de sodium $(\ce{Na^+ + CH3COO^-})$. La solution a un volume $V_0 = \pu{100 mL}$ et une masse $m = \pu{130 g}$. La solution $S_0$ contenue dans la chaufferette chimique étant trop concentrée pour être dosée directement au laboratoire, on prépare une solution $S_1$ en diluant 100 fois le contenu de la chaufferette chimique.
Pour déterminer la concentration molaire $C_0$ en éthanoate de sodium apporté dans une chaufferette chimique, on place dans un bécher un volume $V_1 = \pu{25,0 mL}$ de solution $S_1$ à titrer.
On réalise le titrage avec suivi pH-métrique de la solution $S_1$ par une solution d’acide chlorhydrique $(\ce{H3O^+ + Cl^-(aq)})$ de concentration $C_A = \pu{2,0e-1 mol.L-1}$. On note $V_A$ le volume de la solution d’acide chlorhydrique versé.
- Écrire l’équation de la réaction chimique support de ce titrage.
Réponse
$$ \ce{ CH3COO^-(aq) + H3O^+ -> CH3COOH(aq) + H2O } $$
On obtient les courbes de la figure 5 ci-dessous :
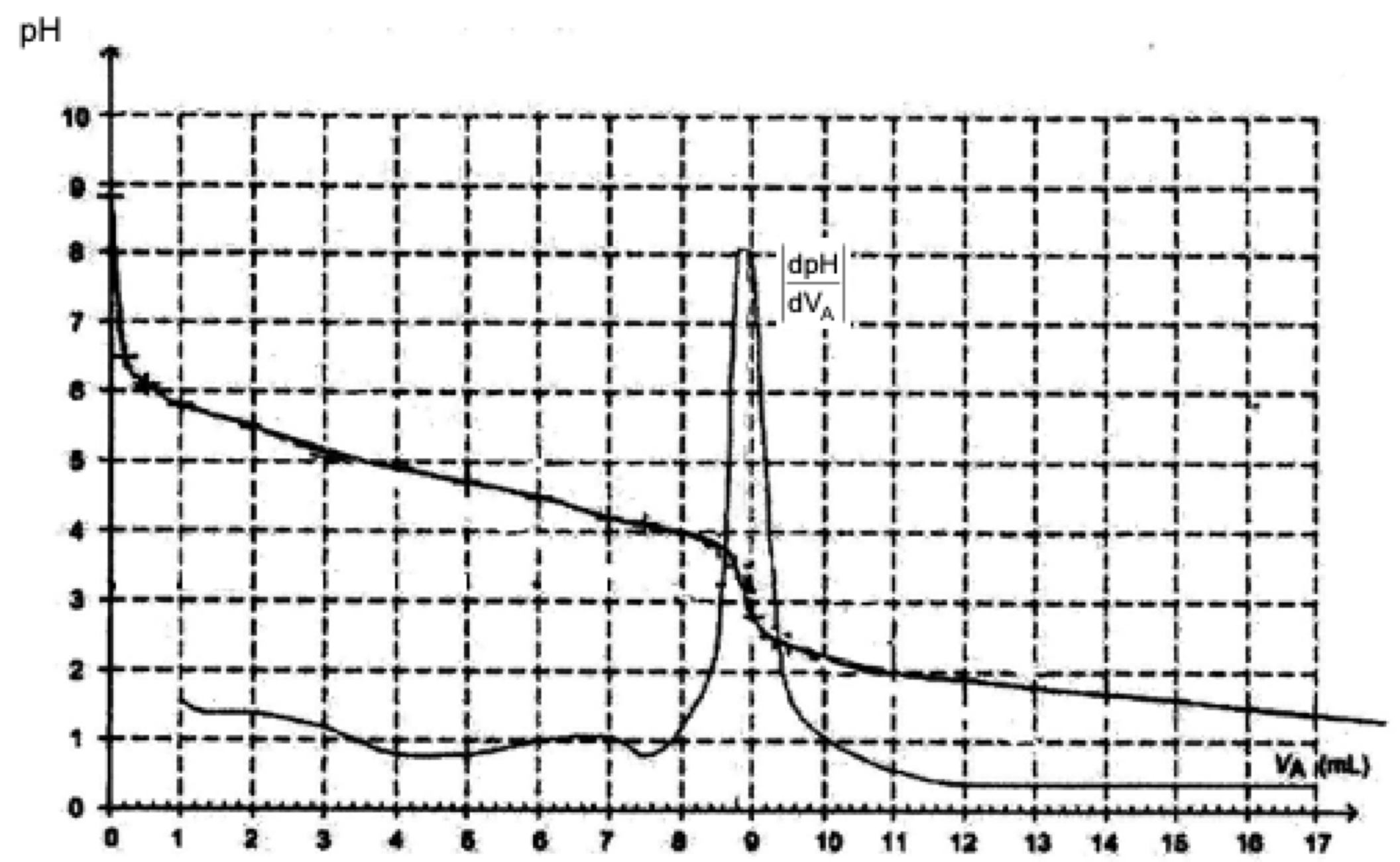
Remarque : Image à télécharger
- Schématiser et légender le dispositif de titrage.
Réponse
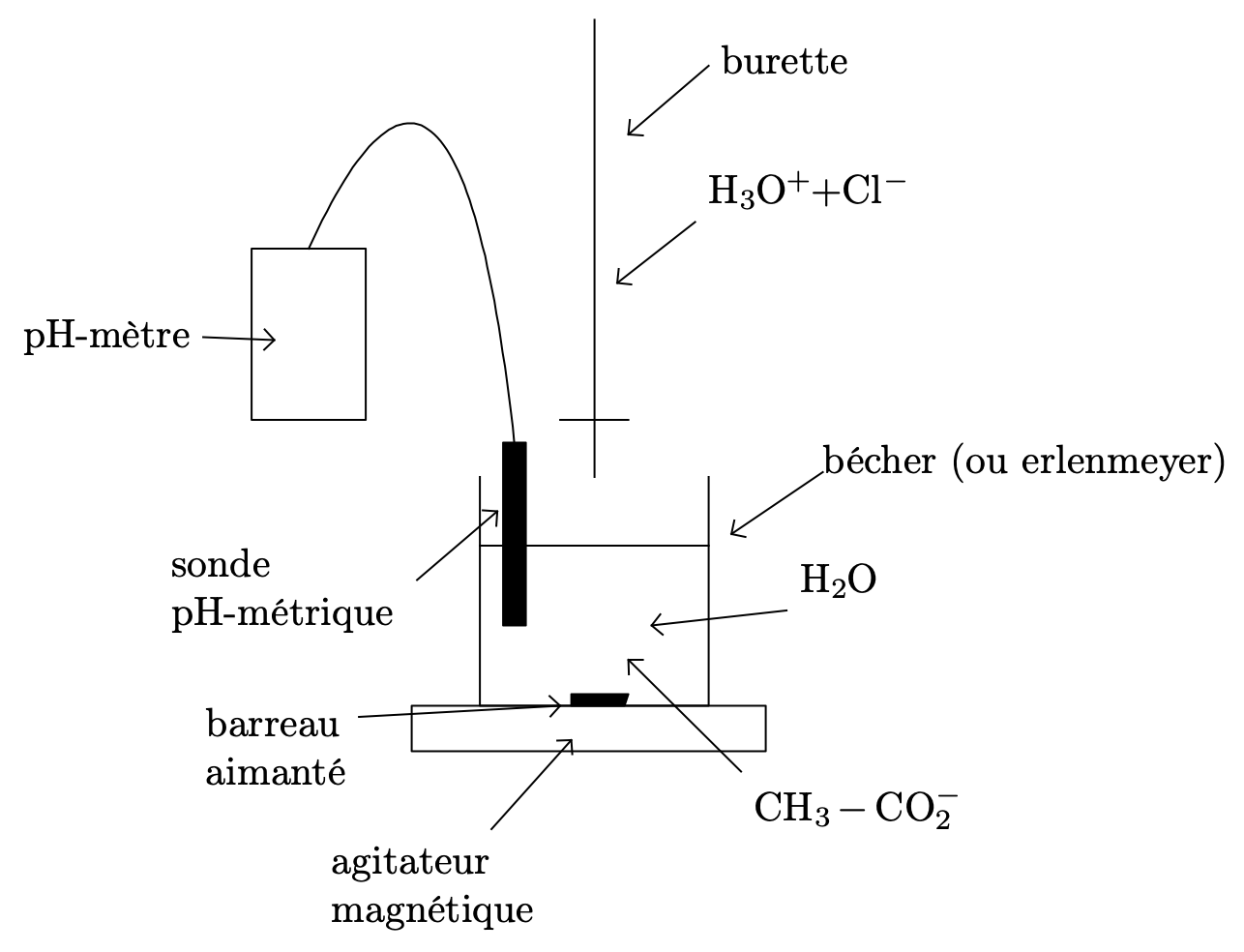
- Donner la définition de l’équivalence d’un titrage.
Réponse
L’équivalence d’un titrage est l’instant du titrage où on change de réactif limitant.
- Écrire la relation entre la quantité de matière d’ions éthanoate $n_i(\ce{CH3COO^-})$ présente initialement dans le bécher et la quantité de matière d’ions oxonium $n_E(\ce{H3O^+})$, qui permet d’atteindre cette équivalence. On pourra éventuellement s’aider d’un tableau d’avancement.
Réponse
L’utilisation d’un tableau d’avancement permet d’écrire qu’à l’équivalence :
- $n_i(\ce{CH3COO^-}) - x_E = 0$
- $n_E(\ce{H3O^+}) - x_E = 0$
donc $x_E = n_i(\ce{CH3COO^-}) = n_E(\ce{H3O^+})$.
- Déterminer le volume à l’équivalence $V_{AE}$ en expliquant la méthode utilisée.
Réponse
Pour déterminer la valeur de $V_{AE}$, on utilise la méthode de la dérivée, sur le graphique donnant l’évolution du pH au cours du temps. Il faut noter que le concepteur du sujet a décidé de tracer $ \left\lvert \dfrac{\mathrm{d}pH}{\mathrm{dV_A}} \right\rvert $. C’est la raison pour laquelle les valeurs de cette fonction sont toutes positives alors que la dérivée est, elle, négative puisque la fonction $pH = f(V_A)$ est décroissante. $V_{AE} = \pu{8,8 mL}$.
- Calculer la concentration $C_1$ en ions éthanoate de la solution dosée.
Réponse
-
$x_E = n_i(\ce{CH3COO^-}) = n_E(\ce{H3O^+}) \Leftrightarrow \boxed{ C_1V_1 = C_A V_{AE} }$.
-
Finalement $\boxed{ C_1 = C_A \dfrac{V_{AE}}{V_1} }$.
A.N. $C_1 = \pu{2,0e-1 mol.L-1} \times \dfrac{\pu{8,8 mL}}{\pu{25,0 mL}} = \pu{7,0e-2 mol.L-1}$.
- Calculer la concentration $C_0$ en éthanoate de sodium apporté dans la solution contenue dans la chaufferette. La solution d’éthanoate de sodium contenue dans la chaufferette est-elle saturée ?
Réponse
- $C_O = 100 C_1$, donc $C_0 = 100 \times \pu{7,0e-2 mol.L-1} = \pu{7,0 mol.L-1}$.
- L’énoncé annonce que la solubilité de l’éthanoate de sodium est égale à $s = \pu{4,5 mol.L-1} < \pu{7,0 mol.L-1}$. La solution est donc saturée.
- Calculer la masse d’éthanoate de sodium dans la chaufferette.
Réponse
- Concentration massique en éthanoate de soldium : $m(\ce{CH3COONa}) = C_0 \, V\, M(\ce{CH3COONa}) = \pu{7,0 mol.L-1} \times \pu{1,00e-1 L} \times \pu{82,0 g.mol-1} = \pu{5,8e1 g}$.
- La solution aqueuse de masse $\pu{130 g}$ contenue dans la chaufferette est-elle au moins à 20 % en masse d’éthanoate de sodium comme l’indique le texte introductif ?
Réponse
- $\dfrac{ m(\ce{CH3COONa}) }{ m } = \dfrac{ \pu{5,8e1 g} }{ \pu{130 g} } = \pu{0,44} $ soit 44 %. Ce pourcentage est supérieur à 20 %, l’énoncé est donc correct.