La pièce de 5 centimes d’euro est composée d’un centre en acier (constitué essentiellement de fer et de carbone) entouré de cuivre. Elle a un diamètre de $\pu{21,25 mm}$, une épaisseur de $\pu{1,67 mm}$ et une masse de $\pu{3,93 g}$.
On cherche par une méthode spectrophotométrique à déterminer la teneur en cuivre d’une telle pièce.
Le cuivre, de masse molaire $\pu{63,5 g.mol-1}$, est un métal qui peut être totalement oxydé en ions cuivre (II) par un oxydant puissant tel que l’acide nitrique selon la réaction d’équation :
$$
\ce{3 Cu(s) + 8 H^+(aq) + 2 NO3^-(aq) -> 3 Cu^{2+}(aq) + 4 H2O(l) + 2 NO(g)}
$$
Les ions cuivre (II) formés se retrouvent intégralement dissous en solution ; le monoxyde d’azote $\ce{NO}$ est un gaz peu soluble dans l’eau.
En pratique, on dépose une pièce de 5 centimes dans un erlenmeyer de $\pu{100 mL}$, on place cet erlenmeyer sous la hotte et on met en fonctionnement la ventilation. Équipé de gants et de lunettes de protection, on verse dans l’erlenmeyer $\pu{20 mL}$ d’une solution d’acide nitrique d’une concentration environ égale à $\pu{7 mol.L-1}$.
La pièce est alors assez vite oxydée et on obtient une solution notée $S_1$.
On transfère intégralement cette solution $S_1$ dans une fiole jaugée de $\pu{100 mL}$ et on complète cette dernière avec de l’eau distillée jusqu’au trait de jauge. On obtient une solution $S_2$ qui contient également des ions fer (III) provenant de la réaction entre l’acide nitrique et le fer contenu dans le centre d’acier de la pièce.
L’absorbance de la solution $S_2$ à $\pu{800 nm}$ est mesurée, elle vaut $A = \pu{0,575}$.
Étalonnage
- Déterminer, en argumentant votre réponse, les couleurs attendues pour une solution d’ions cuivre(II) et pour une solution d’ions fer (III). Pour quelle raison choisit-on de travailler à une longueur d’onde de 800 nm ?
Réponse
Dans le cas où une solution absorbe dans un seul domaine de longueur d’onde, sa couleur perçue est la couleur complémentaire de celle des radiations absorbées. Ainsi, une solution d’ions cuivre (II) est de couleur bleu-vert car elle absorbe principalement dans le rouge (entre 647 et 850 nm). De même, une solution d’ions fer (III) est de couleur jaune-vert car elle absorbe principalement dans le violet (entre 400 et 424 nm).
En travaillant à 800 nm, on est sûr que les ions fer (III) n’absorbent pas la lumière et donc que l’absorbance mesurée est uniquement due aux ions cuivre (II).
- On fait subir à différents échantillons de métal cuivre pur le même traitement que celui décrit ci-dessus pour la pièce. On obtient alors des solutions d’ions cuivre (II) dont on mesure l’absorbance à 800 nm.
Montrer, en utilisant le document 2 et en complétant l’ANNEXE À RENDRE AVEC LA COPIE, que la loi de Beer-Lambert est vérifiée pour ces solutions d’ions cuivre (II).
Réponse
Lorsque la loi de Beer-Lambert est vérifiée, l’absorbance de la solution est proportionnelle à la concentration de l’espèce colorée : $A = k \cdot c$.
En traçant la courbe $A=f(\text{concentration})$, on obtient une droite passant par l’origine, ce qui correspond bien à une situation de proportionnalité.
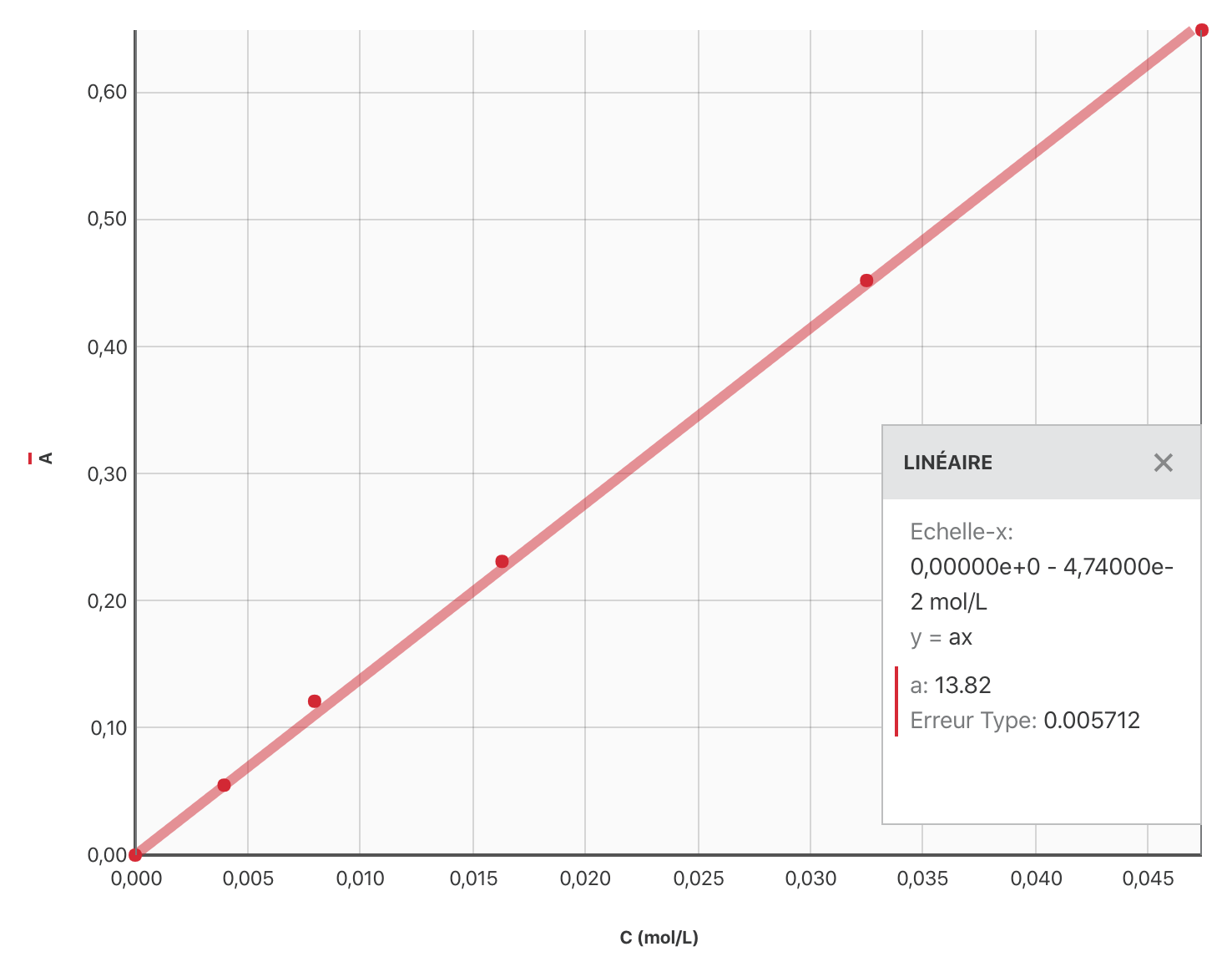
Détermination de la teneur en cuivre dans la pièce
- Déterminer la masse de cuivre contenue dans la pièce de 5 centimes d’euro.
Réponse
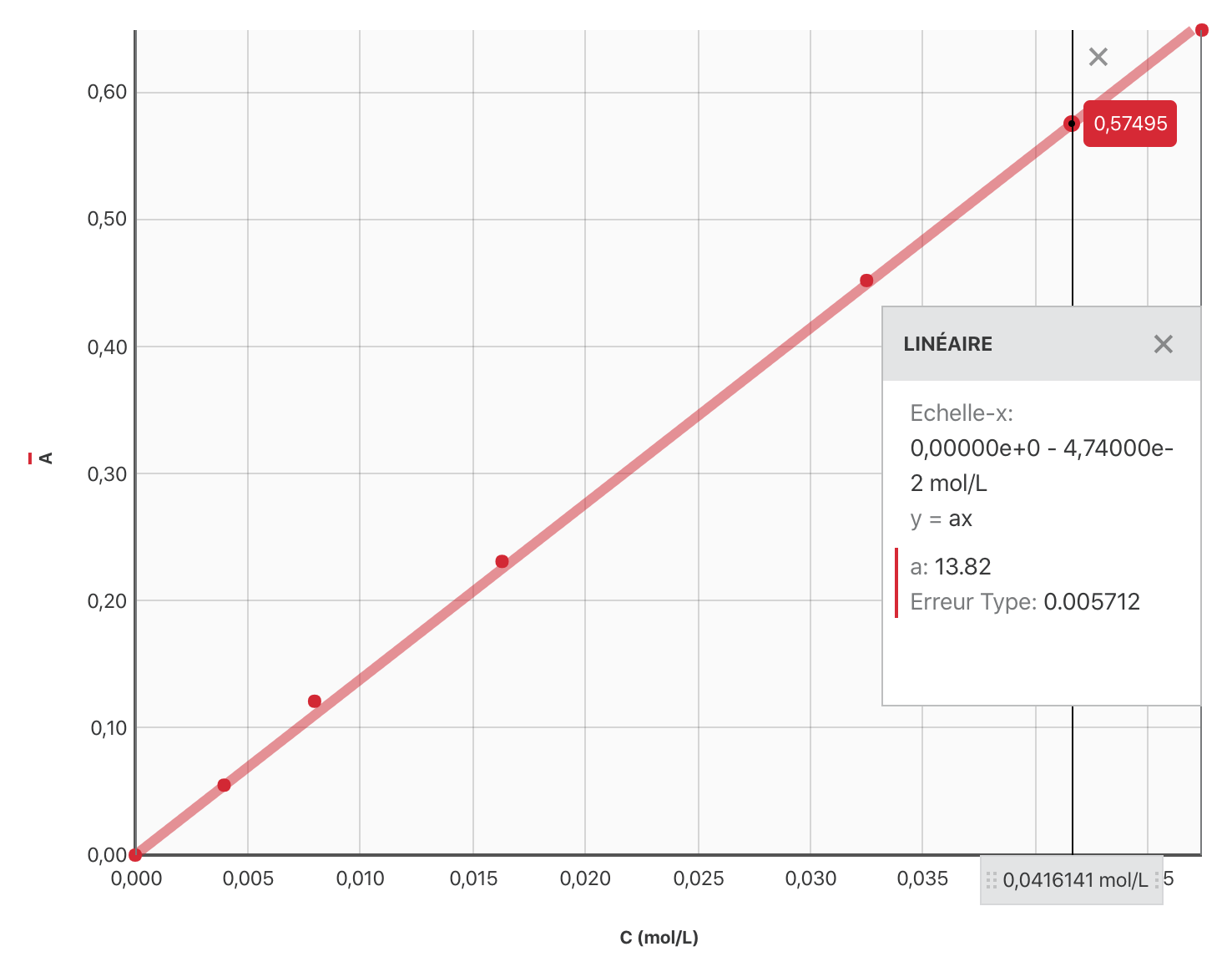On constate donc que $[ \ce{Cu^{2+}} ]_f = \pu{4,2e-2 mol.L-1}$.
Comme la transformation chimique est totale, un bilan de matière, à l’aide d’un tableau d’avancement, donne :
- $n_f (\ce{Cu}) = n_0 (\ce{Cu}) - 3 x_{text{max}} = 0$ ;
- $n_f (\ce{Cu^{2+}}) = 3 x_{text{max}} = [ \ce{Cu^{2+}} ]f \cdot V{\text{sol}} $ où $V_{\text{sol}}$ est le volume de la solution $S_2$.
Donc $n_0 (\ce{Cu}) = [ \ce{Cu^{2+}} ]_f \cdot V_{\text{sol}} $ et $m_0 (\ce{Cu}) = [ \ce{Cu^{2+}} ]_f \cdot V_{\text{sol}} \cdot M(\ce{Cu}) $. A.N. $m_0 (\ce{Cu}) = \pu{4,2e-2 mol.L-1} \times \pu{100e-3 L} \times \pu{63,5 g.mol-1} = \pu{2,7e-1 g}$.
- En déduire la teneur (ou « pourcentage massique ») en cuivre dans la pièce.
Réponse
$t = \dfrac{m(\ce{Cu})}{m_{\text{pièce}}}$. Donc $t = \dfrac{ \pu{2,7e-1 g} }{ \pu{3,93 g}} = \pu{6,9e-2}$ soit 6,9 %.
Incertitude
10 groupes d’élèves ont déterminé expérimentalement la masse de cuivre présente dans 10 pièces de 5 centimes de même masse. Leurs résultats sont les suivants :
| Groupe | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Masse de cuivre (mg) | 260 | 270 | 265 | 263 | 264 | 265 | 262 | 261 | 269 | 267 |
- Déterminer, grâce aux valeurs trouvées par les élèves, l’incertitude élargie $U(m)$ (pour un niveau de confiance de 95 %) sur la mesure de la masse de cuivre dans une pièce.
Réponse
- La moyenne des dix mesures vaut $\bar{m} = \pu{264,6 mg}$ ;
- L’écart-type des 10 mesures vaut $\sigma_{n-1} = \pu{3,31 mg}$. Comme $U(m) = k \dfrac{\sigma_{n-1}}{\sqrt{n}}$, avec $k$ le coefficient d’élargissement pour un niveau de confiance de 95 %, $U(m) = \pu{2,26} \times \dfrac{\pu{3,31 mg}}{\sqrt{10}} = \pu{2,4 mg} = \pu{3 mg}$.
- En déduire l’intervalle dans lequel devrait se situer le résultat du mesurage de la masse de cuivre avec un niveau de confiance de 95 %.
Réponse
À partir de la réponse à la question précédente, on peut conclure que $m = \pu{265 \pm 3) mg}$. L’encadrement de la solution est donc $\pu{262 mg} \leqslant m \leqslant \pu{268 mg}$.
Documents
Spectres d’absorption des ions cuivre (II) et fer (III) dans l’eau
On donne ci-dessous les spectres d’absorption d’une solution d’ions cuivre (II) et d’une solution d’ions fer (III), ainsi qu’un tableau reliant longueur d’onde d’absorption et couleur complémentaire. Le « blanc » a été fait avec de l’eau pure.
Solution aqueuse d’ions cuivre (II) $\ce{Cu^{2+}}$ de concentration $\pu{7,5e-3 mol.L-1}$.
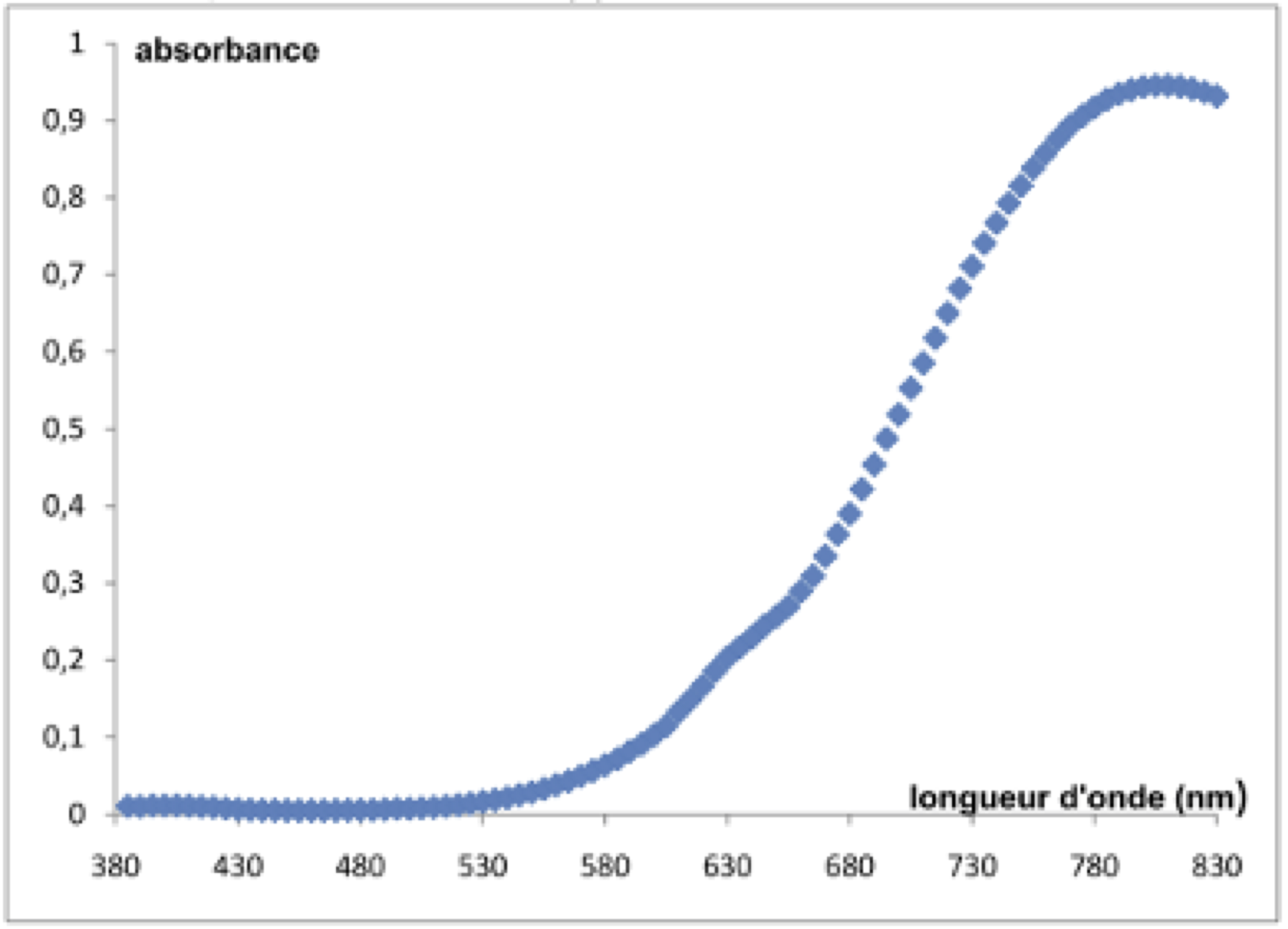
Solution aqueuse d’ions fer (III) $\ce{Fe^{3+}}$ de concentration $\pu{5,0e-2 mol.L-1}$.
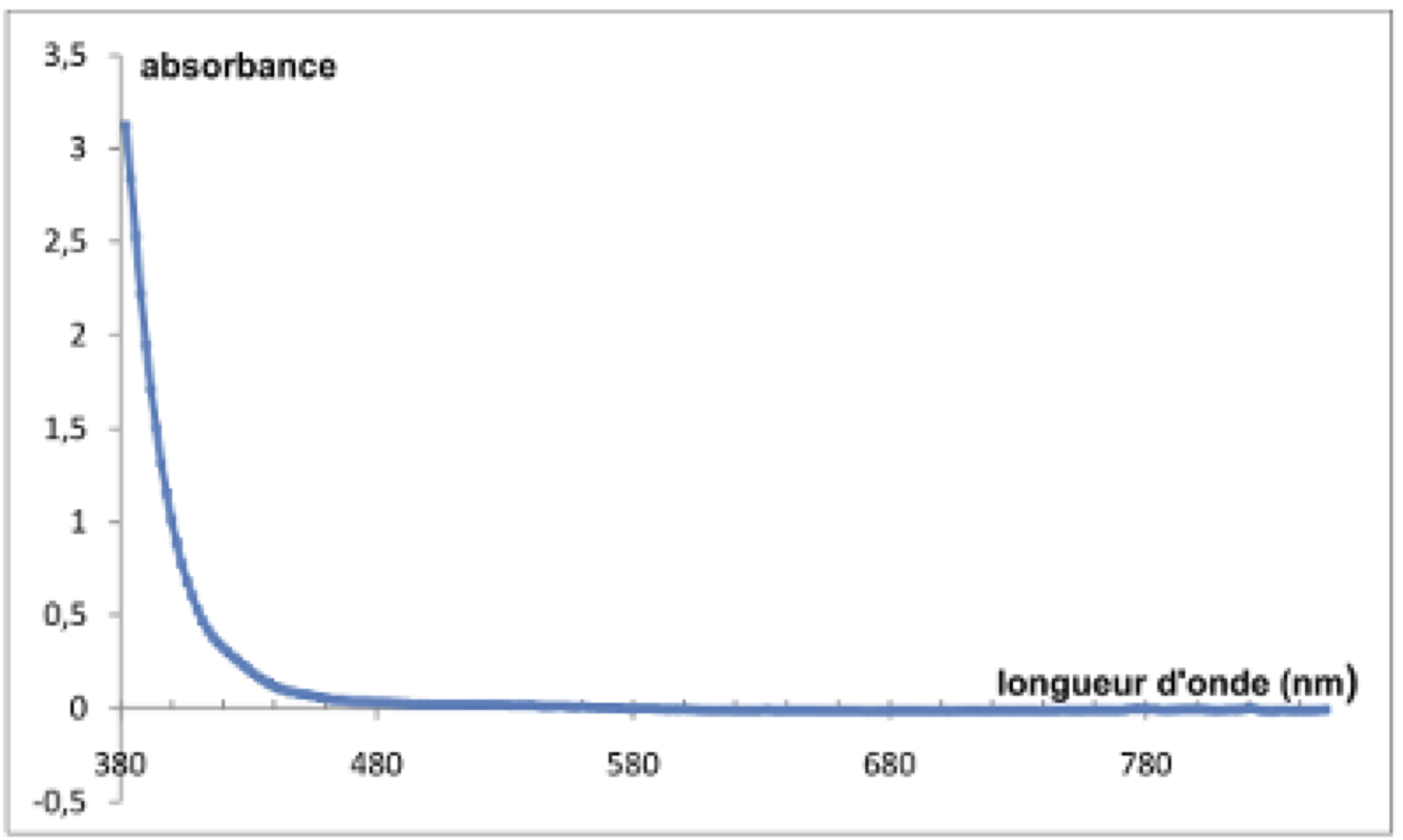
| Couleur absorbée | violet | bleu | vert | jaune | orange | Rouge |
|---|---|---|---|---|---|---|
| Longueur d’onde d’absorption (nm) | 400-424 | 424-491 | 491-575 | 575-585 | 585-647 | 647-850 |
| Couleur complémentaire | jaune-vert | jaune | pourpre | bleu | vert-bleu | bleu-vert |
Courbe d’étalonnage
Tableau donnant l’absorbance $A$ à $\pu{800 nm}$ de solutions aqueuses contenant des ions cuivre (II), obtenues à partir de divers échantillons de métal cuivre pur :
| Masse de l’échantillon de cuivre (mg) | 0 | 25,1 | 50,6 | 103,8 | 206,2 | 300,6 |
| Concentration ($\pu{mol.L-1}$) | $\pu{0,00}$ | $\pu{3,95e-3}$ | $\pu{7,97e-3}$ | $\pu{1,63e-2}$ | $\pu{3,25e-2}$ | $\pu{4,74e-2}$ |
| Absorbance | 0 | 0,055 | 0,121 | 0,231 | 0,452 | 0,649 |
Incertitude sur un mesurage
On rappelle les différentes formules intervenant dans la détermination de l‘incertitude sur le résultat du mesurage d’un ensemble de $n$ valeurs ${x_1, x_2, \ldots, x_n}$ :
- Écart-type : $\sigma_{n-1} = \sqrt{ \dfrac{ \sum_{i=1}^{n} (x_i - \bar{x})^2 }{ n-1 } }$
- Incertitude-type sur la moyenne : $ u(\bar{x}) = \dfrac{ \sigma_{n-1} }{ \sqrt{n} }$
- Incertitude élargie sur la moyenne : $ U(\bar{x}) = k\, u(\bar{x}) $ avec :
- $k = 1$ pour un niveau de confiance de 68 % ;
- $k = 2$ pour un niveau de confiance de 95 % ;
- $k = 3$ pour un niveau de confiance de 98 %.