L’objectif de ce document est de comprendre pourquoi l’effet photoélectrique est une preuve expérimentale de l’existence du photon.
« La découverte et l’étude du phénomène photoélectrique a réservé aux physiciens une très grande surprise. Ce phénomène consiste en ceci qu’un morceau de matière exposé à l’action d’une radiation de longueur d’onde suffisamment courte projette souvent autour de lui des électrons en mouvement rapide. La caractéristique essentielle du phénomène est que l’énergie des électrons expulsés est uniquement fonction de la fréquence de la radiation incidente et ne dépend nullement de son intensité. Seul le nombre des électrons dépend de l’intensité incidente. Ces lois empiriques simples rendaient très pénibles l’interprétation théorique du mécanisme élémentaire aboutissant à la libération des électrons photoélectriques, des photoélectrons comme on dit aujourd’hui. La théorie ondulatoire de la lumière qui paraissait vers 1900 reposait sur des bases inébranlables conduit à considérer l’énergie radiante comme répartie uniformément dans l’onde lumineuse. Un électron frappé par une onde lumineuse reçoit donc l’énergie radiante d’une façon continue et la quantité d’énergie qu’il reçoit ainsi par seconde est proportionnelle à l’intensité de l’onde incidente et ne dépend nullement de la longueur d’onde. Les lois de l’effet photoélectrique paraissaient donc bien difficiles à expliquer.
M. Einstein a eu, en 1905, l’idée très remarquable que les lois de l’effet photoélectrique indiquent l’existence pour la lumière d’une structure discontinue où les quanta interviennent. […] M. Einstein a donc admis que toute radiation monochromatique est divisée en grains dont l’énergie a une valeur proportionnelle à la fréquence, la constante de proportionnalité étant bien entendu la constante de Planck. Dès lors, les lois de l’effet photoélectrique s’interprètent aisément. Lorsqu’un électron contenu dans la matière recevra un grain de lumière, il pourra absorber l’énergie de ce grain et sortir de la matière où il était enfermé, à condition toutefois que l’énergie du grain de lumière soit supérieure au travail nécessaire à l’électron pour sortir de la matière. L’électron ainsi expulsé par l’action de la lumière possédera donc une énergie cinétique égale à l’énergie du grain de lumière absorbée diminuée du travail dépensé pour sortir de la matière : cette énergie cinétique sera donc une fonction linéaire de la fréquence de la radiation incidente, le coefficient angulaire de la droite qui la représente en fonction de la fréquence étant numériquement égal à la constante de Planck. Toutes ces prévisions se sont montrées en parfait accord avec l’expérience. ».
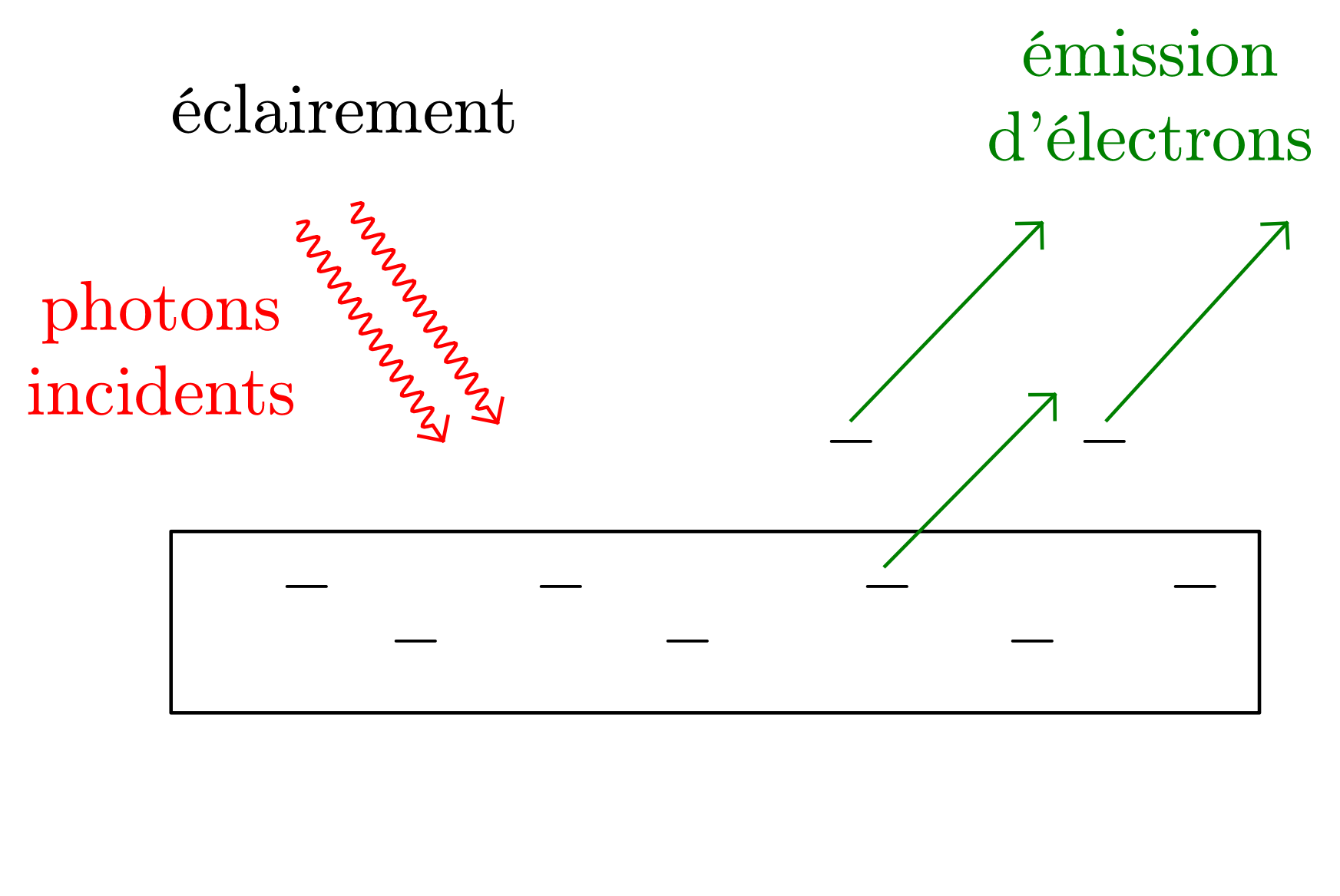
- Pourquoi l’effet photoélectrique décrit dans le texte ne peut-il pas être interprété de manière satisfaisante en physique « classique » ?
Solution
En physique classique l’énergie peut s’accumuler. Si elle n’est initialement pas suffisante, en attendant suffisamment longtemps elle finit par le devenir. Ce n’est pas le cas ici, pour arracher un électron il faut posséder la bonne quantité d’énergie dès le début.
Analogie : pour franchir $\pu{6 m}$ en saut à la perche, il faut posséder la bonne quantité d’énergie au début du saut, on ne peut pas additionner les énergies de 6 sauts de $\pu{1 m}$.
- Comment appelle-t-on les grains d’énergie dont parle Einstein ? Décrire le mécanisme d’échange d’énergie entre le « grain d’énergie » et un atome.
Solution
Un grain d’énergie est un photon. Les photons peuvent être absorbés par les atomes si l’énergie qu’ils transportent est égale à la différence d’énergie entre deux niveaux d’énergie au sein de cet atome.
- On constate expérimentalement que l’effet photoélectrique ne se produit qu’à partir d’une fréquence seuil $\nu_0$ du rayonnement incident. Comment relier l’énergie d’extraction $W_{\text{extraction}}$ de l’électron et la fréquence seuil $\nu_0$ pour un métal donné ?
Solution
Il faut $E_{r_0} = W_{\text{extraction}}$. Comme $E_{r_0}= h\, \nu_0$, $$ h\, \nu_0 = W_{\text{extraction}} \iff \nu_0 =\dfrac{W_{\text{extraction}}}{h} $$
- Justifier l’expression de l’énergie cinétique d’un électron émis par effet photoélectrique : $$ E_C= h\, \nu - W_{\text{extraction}} $$ Indiquer comment Millikan a pu en déduire une valeur précise de la constante de Planck.
Solution
Si $E_r > E_{r_0} \iff E_r - E_{r_0} > 0 \iff h\, \nu - W_{\text{extraction}} > 0$. L’énergie que communique le photon à l’électron est supérieure à l’énergie nécessaire à l’extraction de cet électron du métal. Ce supplément d’énergie se retrouve sous forme d’énergie cinétique : $E_C= h\, \nu - W_{\text{extraction}}$.
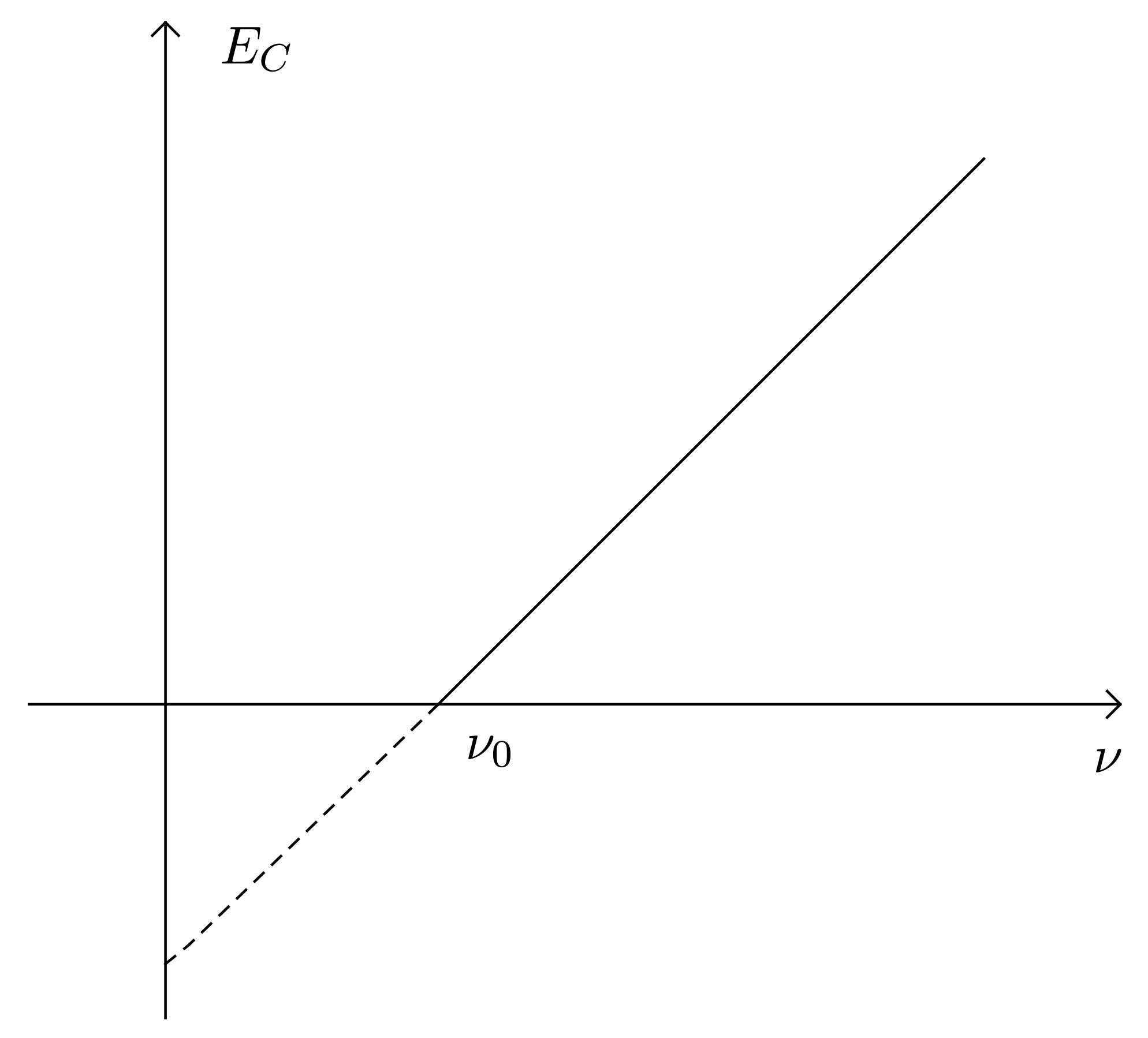
La constante de Planck $k$ représente le coefficient directeur de la droite sur le graphe $E_C = f(\nu)$.
- L’intensité de la lumière étant exprimée en $\pu{W.m-2}$, comment interpréter cette grandeur en termes de « grains d’énergie » ? Comment évolue la quantité d’électrons émis quand on augmente l’intensité du faisceau lumineux incident ?
Solution
L’intensité lumineuse est le nombre de photons qui atteignent une surface de $\pu{1 m2}$ par unité de temps.
Lorsqu’on augmente l’intensité lumineuse d’une source de lumière on augmente le nombre de photons qui sont émis chaque seconde par cette source ; on n’augmente pas l’énergie que transporte chacun de ces photons.