Rayonnement électromagnétique et transfert thermique
Émission, absorption, réflexion, diffusion
Émission
Il s’agit du rayonnement électromagnétique émis par un corps porté à une certaine température. Cette émission est spontanée et a pour cause les mouvements des porteurs de charge de la matière (électrons, etc.) dus à l’excitation thermique. L’énergie interne est ainsi convertie en énergie radiative. Nous notons $\varphi_e$ le flux surfacique correspondant à cette émission.
Absorption
Il s’agit du phénomène inverse. Le rayonnement absorbé par la matière est converti en énergie interne. Nous noterons $\varphi_a$ le flux surfacique absorbé.
Réflexion et diffusion
Le rayonnement incident sur une paroi peut être renvoyé par la paroi dans une autre direction dans le milieu d’incidence par interaction avec la paroi mais sans absorption. Les phénomènes concernés peuvent être la simple réflexion (obéissant aux lois de Descartes) ou la diffusion qui consiste à un renvoi étalé dans toutes les directions même pour une direction incidente unique. Le verre dépoli, le papier, les tissus, etc. sont des substances diffusantes. Réflexion et diffusion s’effectuent sans changement de fréquence des ondes. Notons $\varphi_r$, Ie flux surfacique de retour dans le milieu d’incidence.
Milieux transparents. Milieux opaques
Milieu transparent
Un milieu est dit totalement transparent s’il transmet intégralement le rayonnement qu’il reçoit. Il n’y a donc ni absorption, ni réflexion/diffusion.
Milieu opaque
À l’inverse un milieu est dit totalement opaque s’il ne transmet aucune fraction de rayonnement qu’il reçoit. Le rayonnement incident est donc soit absorbé, soit réfléchi/diffusé, soit les deux.
- Remarque
- En fait, on n’observe jamais une transparence ou une opacité totale sur l’ensemble des fréquences du spectre. Pour un milieu donné, il convient de définir les intervalles de fréquences (ou de longueur d’onde), pour lesquelles on pourra considérer le milieu comme à peu près transparent ou opaque. Ainsi le verre, par exemple, pourra être considéré comme transparent dans l’intervalle $\pu{0,3 \mu m} < \lambda < \pu{3 \mu m}$ et opaque au contraire dans l’intervalle $\pu{4 \mu m} < \lambda < \pu{30 \mu m}$.
Équilibre radiatif d’un corps opaque
Flux surfacique incident
Le flux surfacique incident $\varphi_i$ est la puissance surfacique du rayonnement incident au point considéré. Le corps étant opaque au rayonnement, ce rayonnement incident est soit absorbé, soit réfléchi/diffusé, ces processus pouvant avoir lieu simultanément. La conservation de l’énergie exige dans ces conditions que : $$ \varphi_i = \varphi_a + \varphi_r $$
Flux surfacique partant
Le flux surfacique partant $\varphi_p$ cumule le flux $\varphi_r$, mais aussi le flux émis $\varphi_e$ par le corps au voisinage de la frontière. La conservation de l’énergie implique que : $$ \varphi_p = \varphi_e + \varphi_r $$
- Remarque
- L’équilibre radiatif ne suppose pas l’équilibre thermodynamique pour les corps opaques, leurs températures peuvent être différentes.
Rayonnement d’équilibre
- Remarque
- L’équilibre thermodynamique nécessite l’équilibre radiatif des corps opaques avec le rayonnement dans lequel ils baignent.
Loi de Stefan pour le rayonnement d’équilibre d’un corps noir
Corps noir
Un corps noir est défini comme un absorbeur intégral sur la totalité du spectre : tout rayonnement thermique incident est absorbé quel que soit sa longueur d’onde et quelle que soit sa direction incidente.
Le concept d’absorbeur intégral est un concept idéal. L’absorption totale ou quasi totale pour une substance donnée n’est observée, dans la pratique, que dans certains domaines spectraux ou « fenêtres spectrale ».
Le flux partant d’un corps noir est totalement d’origine émissive : il n’y a pas de contribution due au rayonnement réfléchi ou diffusé.
Loi de Stefan
La loi de Joseph Stefan fut découverte expérimentalement en 1879 lors de son étude du rayonnement d’équilibre du corps noir. Elle stipule que le flux émis par un corps noir est proportionnel à sa température élevée à la puissance 4. $$ \varphi_e = \sigma T^4 $$ avec $\sigma = \pu{5,670e8 W.m-2.K-4}$.
Un corps noir émet un flux surfacique, à toutes les longueurs d’ondes, d’autant plus grand que sa température est élevée.
Bilan radiatif pour un corps noir
Le bilan radiatif d’un corps noir en équilibre radiatif et thermodynamique est : $$ \varphi_e = \varphi_a = \sigma T^4 $$ avec $\sigma = \pu{5,670e-8 W.m-2.K-4}$.
- Remarque
- On attribue souvent les propriétés des corps noirs en équilibre radiatif et thermodynamique aux corps noirs en équilibre radiatif à température localement constante (mais pas uniforme). Si on considère, par exemple, le soleil, l’étude du rayonnement qu’il émet montre qu’il est voisin de celui d’un corps noir de température de l’ordre de $\pu{6000 °C}$. La couche superficielle responsable de l’émission est appelée photosphère. Sa température d’équilibre local est voisine de cette valeur. Quant aux rayonnements émis par les couches profondes du soleil (dont la température est beaucoup plus élevée, de l’ordre de $\pu{10^7 K}$) ils sont totalement absorbés par la photosphère.
Effet de serre
On étudie l’effet de serre produit par l’interposition d’une vitre au-dessus d’une plaque qui reçoit le rayonnement solaire. La plaque est noircie et assimilée à un corps noir. Le verre est supposé totalement transparent au rayonnement solaire. La vitre est en revanche totalement absorbante pour le rayonnement infrarouge émis par la plaque (et l’atmosphère) qui absorbe le rayonnement solaire. On désigne par $\varphi_s$ le flux solaire surfacique supposé arriver normalement à la vitre et à la plaque, par $\varphi_{CN}$ le rayonnement émis par la plaque et par $\varphi_1$ le rayonnement émis par la vitre.
Donnée
- $\varphi_s = \pu{0,600 kW⋅m−2}$.
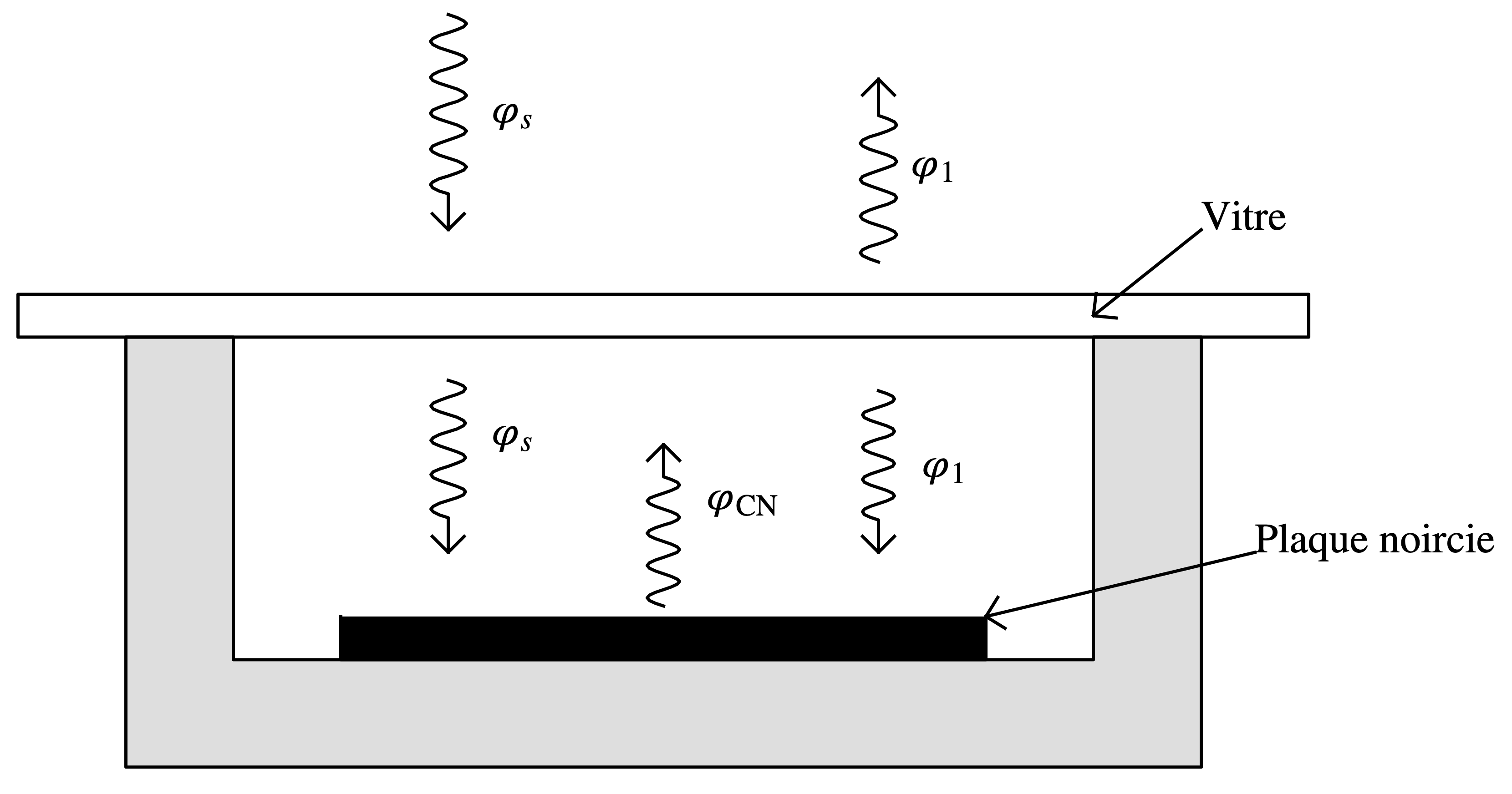
- On suppose l’équilibre radiatif de la plaque. Écrire l’équation qui traduit cet équilibre.
Réponse
Puisque la plaque peut être considérée comme un corps noir,
- le flux surfacique incident sur la plaque est $\varphi_i = \varphi_s + \varphi_1$ ;
- le flux surfacique partant sur la plaque est $\varphi_p = \varphi_{CN}$
L’équilibre radiatif de la plaque impose donc $$ \varphi_s + \varphi_1 = \varphi_{CN} $$
- On suppose l’équilibre radiatif de la vitre. Écrire l’équation qui traduit cet équilibre.
Réponse
Puisque la vitre peut être considérée comme un corps noir pour le rayonnement IR,
- le flux surfacique incident est $\varphi_i’ = \varphi_{CN}$ ;
- le flux surfacique partant est $\varphi_p’ = 2 \varphi_1$. Le flux $\varphi_1$ intervient deux fois car la vitre présente deux surfaces au niveau desquelles elle peut rayonner.
L’équilibre radiatif de la vitre impose donc $$ 2 \varphi_1 = \varphi_{CN} $$
- Calculer la température $T$ de la plaque noircie.
Réponse
Si on considère $\varphi_s$ comme une donnée du problème, les équations précédentes constituent un système de deux équations à deux inconnues : $\varphi_1$ et $\varphi_{CN}$. Par substitution, on détermine que $$ \varphi_{CN} = 2\varphi_s $$ Si on applique la loi de Stefan à la plaque, corps noir en équilibre radiatif et thermique local, on peut écrire $$ \varphi_{CN} = \sigma T^4 $$ donc $$ T= \left( \dfrac{2 \varphi_s}{σ} \right)^{1/4} $$
A.N. $ T= \left( \dfrac{2 \times \pu{0,600e3 W⋅m-2} }{\pu{5,670e-8 W⋅m-2⋅K-4}} \right)^{1/4} = \pu{380 K} $.
- En déduire la température $T_1$ de la vitre.
Réponse
L’équation (2) indique que
$$ \varphi_{1} = \dfrac{\varphi_{CN}}{2} $$
Si on applique la loi de Stephan à la vitre, corps noir en équilibre thermodynamique et local pour le rayonnement IR, on peut écrire
$$ \varphi_{1} = \sigma T_{1}^4 $$
donc
$$ T_{1} = \left( \dfrac{\varphi _{1}}{\sigma} \right)^{1 / 4} = \left( \dfrac{\varphi _{CN}}{2 \sigma} \right)^{1 / 4} = \left( \dfrac{T}{2} \right)^{1 / 4} $$
A.N. $T_{1} = \left( \dfrac{\pu{380 K}}{2} \right)^{1 / 4} = \pu{320 K}$.
- On superpose maintenant deux vitres (avec une couche d’air entre ces vitres). Reprendre les questions précédentes et déterminer la nouvelle température de la plaque.
Réponse
Les bilans radiatifs sont les suivants :
- Pour la vitre extérieure : $$ 2 \varphi _{2} = \varphi _{1} $$
- Pour la vitre interieure : $$ 2 \varphi _{1} = \varphi _{2} + \varphi _{CN} $$
- Pour la plaque : $$ \varphi _{CN} = \varphi _{s} + \varphi _{1} $$
On en déduit
$$\varphi_2 = \varphi_s$$ $$\varphi_1=2 \varphi_s$$ $$\varphi_{CN} = 3\varphi_s$$
Si on applique la loi de Stefan à la plaque, corps noir en équilibre radiatif et thermique local, on peut écrire
$$ \varphi _{CN} = \sigma T^4 $$
donc
$$ T = \left( \dfrac{3 \varphi _{s}}{\sigma} \right)^{1 / 4} $$
L’application numérique donne $T = \pu{422 K}$.
- Généraliser le cas précédent à la situation où on utiliserait $n$ vitres.
Réponse
Si on utilise $n$ vitres, $\varphi _{CN} = (n + 1) \varphi _{s}$ et $T = \left( \dfrac{(n + 1) \varphi _{s}}{\sigma} \right)^{1 / 4} $.
- Remarque
- Dans la réalité, chaque vitre réfléchit et absorbe une partie du rayonnement solaire. On peut montrer qu’il faut 4 à 5 vitres pour que la température $T$ soit maximale.