Une solution commerciale $S_0$ d’ammoniac $\ce{NH3 (aq)}$ de concentration $C_0 = \pu{1,1 mol.L-1}$ peut être utilisée, après dilution, comme produit nettoyant (éviers, lavabos, …) ou comme produit détachant (moquette, tapis, …).
On se propose d’étudier la solution $S$ d’ammoniac de concentration $C_S$ : $S$ étant 100 fois plus diluée que $S_0$.
Données :
-
Produit ionique de l’eau : $K_e = \pu{1,0e–14}$.
-
$\text{pK}_a$ de quelques couples acide/base :
- $\ce{H3O+/H2O}$ : $\text{pK}_{a1} = \pu{0,0}$ ;
- $\ce{NH4^+/NH3}$ : $\text{pK}_{a2} = \pu{9,2}$ ;
- $\ce{H2O/HO–}$ : $\text{pK}_{a3} = \pu{14,0}$.
-
Valeurs des conductivités molaires ioniques (en $\pu{S.m2.mol-1}$) :
- $\lambda(\ce{HO–}) = \pu{199e–4 S.m2.mol-1}$ ;
- $\lambda(\ce{NH4^+}) = \pu{73,4e–4 S.m2.mol-1}$.
Préparation de la solution diluée $S$
- Faire la liste de la verrerie nécessaire pour préparer précisément un volume $V = \pu{1,00 L}$ de $S$ à partir de $S_0$.
Titrage de la solution diluée $S$
On se propose de vérifier la valeur de la concentration $C_0$ de $S_0$.
Pour cela, la solution $S$ est titrée par une solution d’acide chlorhydrique de concentration $C_a = \pu{0,015 mol.L-1}$.
Dans un volume $V_S = \pu{20 mL}$ de la solution $S$, on verse progressivement la solution d’acide chlorhydrique et on mesure après chaque ajout le $\text{pH}$ du mélange.
On peut alors tracer la courbe d’évolution du $\text{pH}$ en fonction du volume de solution acide ajoutée $V_a$ à l’aide d’un logiciel approprié. On trace aussi la courbe
d’évolution de la dérivée $\dfrac{\mathrm{dpH}}{\mathrm{dV}_a}$ en fonction de $V_a$.
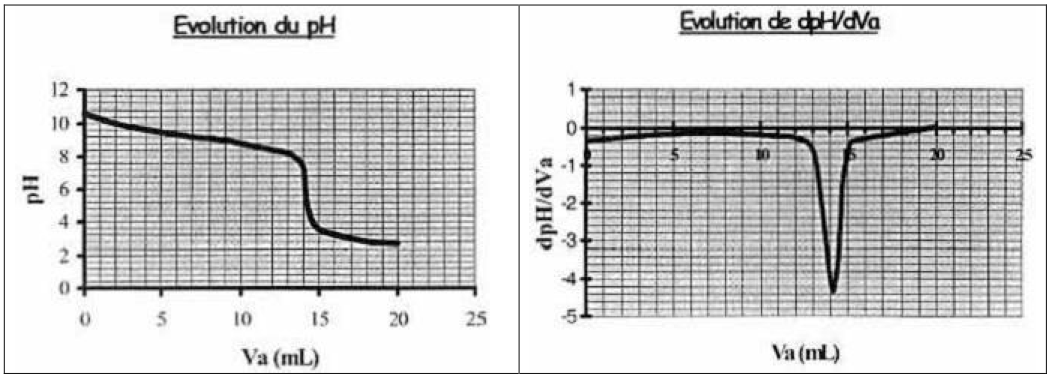
-
Faire un schéma légendé du dispositif expérimental de titrage.
-
Écrire l’équation bilan de la réaction de titrage (1) de la solution d’ammoniac $S$.
-
À partir des données expérimentales, déterminer le volume de solution acide versé à l’équivalence $V_{aE}$.
Préciser la méthode employée. -
En déduire la valeur de la concentration $C_S$ de la solution diluée $S$.
Déterminer alors la valeur de la concentration $C_0$ de la solution $S_0$.
Comparer la valeur trouvée à la valeur $C_0$ donnée au début de l’énoncé.
- Remarque :
- Pour la suite de l’exercice, on utilisera la valeur de $C_0$ donnée au début de l’énoncé et la valeur correspondante de $C_S$.
- Parmi les indicateurs colorés du tableau ci-dessous, déterminer celui qu’il faut ajouter à la solution pour procéder le plus efficacement possible au titrage précédent par une méthode colorimétrique. Justifier ce choix.
Qu’observe-t-on autour de l’équivalence dans ce cas ?
| Indicateur coloré | Teinte acide | Zone de virage | Teinte basique |
|---|---|---|---|
| Bleu de bromophénol | Jaune | 3,0 – 4,6 | Bleu-Violet |
| Rouge de méthyle | Rouge | 4,2 – 6,2 | Jaune |
| Rouge de Crésol | Jaune | 7,2 – 8,8 | Rouge |
Étude de l’équilibre dans la solution diluée $S$
On considère maintenant un volume $U_S = \pu{1,0 L}$ de la solution $S$.
L’équation bilan, notée (2), de la réaction entre l’ammoniac et l’eau est : $$ \ce{NH3 (aq) + H2O (l) <=> NH4^+ (aq) + HO– (aq)} $$
-
Donner l’expression littérale de la constante d’équilibre $K$ associée à l’équation de la réaction (2).
-
Exprimer $K$ en fonction de $K_e$ et $K_{a2}$.
Calculer $K$. -
Établir le tableau d’avancement de la réaction en faisant apparaître les état initial (avancement nul) et final (avancement $x_f$).
- Remarques :
- À l’état initial, $[\ce{NH3}]_i = C_S$ (concentration de la solution $S$).
- Le volume de la solution $U_S$ est supposé constant (la dilution est négligée).
- En supposant que $x_f$ est négligeable par rapport au produit $C_S\cdot U_S$, montrer que :
$$ K \approx \dfrac{x_f^2}{C_S\cdot U_S^2 \cdot C^o} $$ où $C^o = \pu{1,00 mol.L-1}$.
- En déduire la valeur $x_f$. L’hypothèse est-elle justifiée ?
La valeur de la conductivité de la solution diluée $S$ est $\sigma = \pu{8,52e–3 S.m-1}$.
-
En déduire la valeur commune de la concentration (en $\pu{mol.L-1}$) des ions $\ce{NH4^+ (aq)}$ et $\ce{HO– (aq)}$ dans la solution $S$.
-
Déterminer alors la valeur du $\text{pH}$ de la solution $S$. Ce résultat est-il en accord avec les données expérimentales ?