Intensité sonore, niveau sonore

Point mathématique : le logarithme décimal

Logarithme

Le logarithme décimal est la fonction réciproque de la fonction $f$ telle que $f(x) = 10^x$ : $$ \forall x>0, y = \log (x) \Leftrightarrow x = 10^y $$ Le logarithme décimal est une fonction croissante et continue. De plus, $$ \lim_{x \to 0^+} = -\infty \text{ et } \lim_{x \to \infty} = +\infty $$

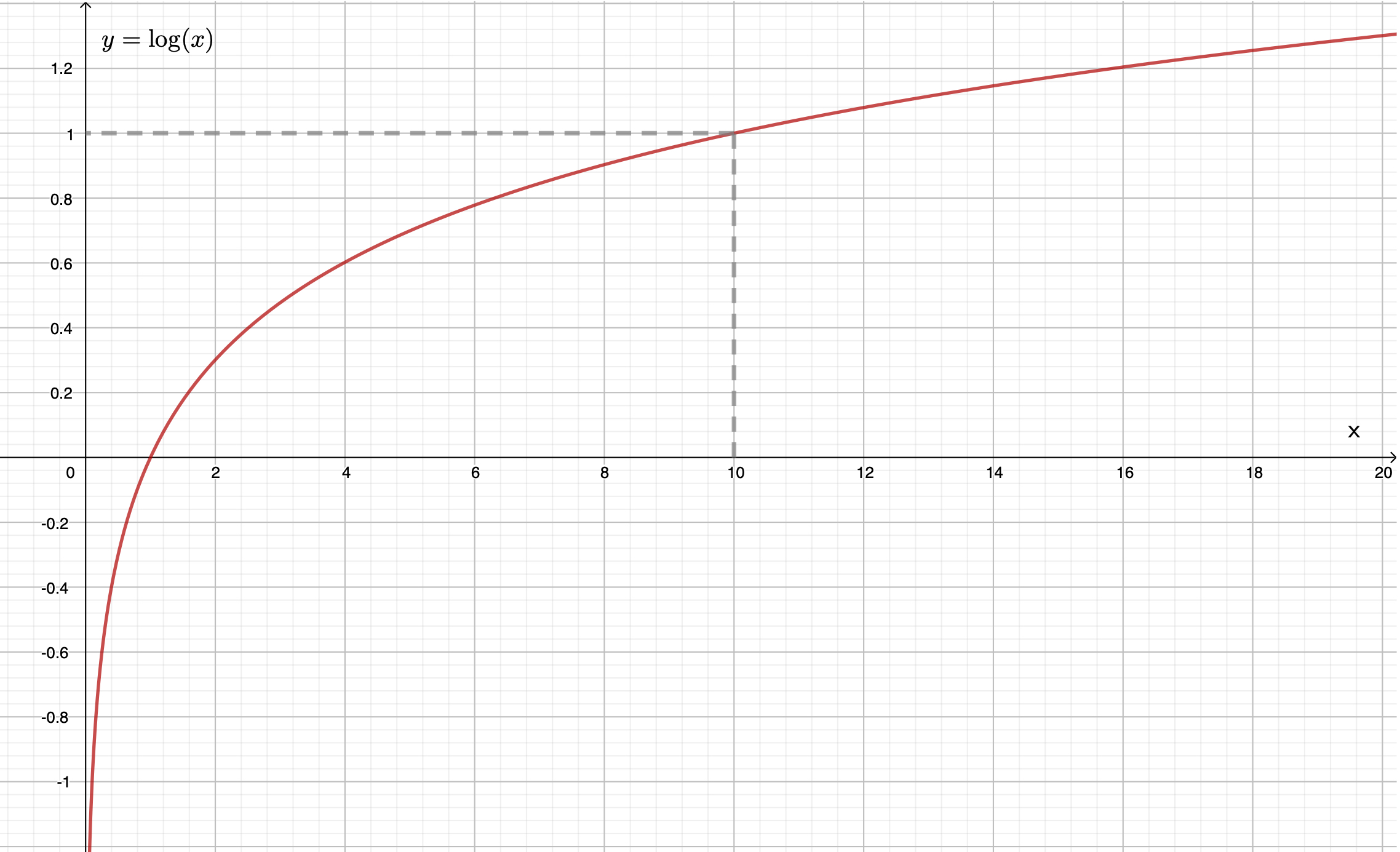> Graphique de la fonction « logarithme décimal »
  1. Commenter l’évolution de la pente de la tangente à la fonction « logarithme décimal » lorsque la valeur de la variable $x$ augmente.
Réponse

La pente, ou coefficient directeur, de la tangente diminue lorsque la variable $x$ augmente.

  1. En déduire comment compléter la phrase suivante : « Pour une variation $\Delta x$ donnée, plus $x$ est grand ……………………… augmente $\log(x)$ (ou plus $\Delta\log (x)$ est ………………..) ».
Réponse

La pente de la tangente est égale à la valeur de la dérivée de la fonction au point considéré, donc :

  • moins vite
  • petit

Propriétés du logarithme décimal

Le logarithme (décimal) est la fonction qui transforme un produit en somme et qui vaut 1 en 10. Ainsi, $$ \log(a\cdot b) = \log(a) + \log(b) $$

$$ \log(10^1) = 1 $$

En utilisant seulement les propriétés du logarithme décimal énoncées ci-dessus, développer les expressions suivantes :

  1. $\log(a^n) = \ldots$
Réponse

$ \log(a^n) = \log(\overbrace{a\times \ldots \times a}^{n \text{fois}}) = \log(a) + \ldots + \log(a) = n\, \log(a)$

  1. $\log(a/b) = \ldots $
Réponse

$\log(a/b) = \log(a \cdot b^{-1}) = \log(a) + \log(b^{-1}) = \log(a) - \log(b)$

  1. $\log(1) = \ldots $
Réponse

$\log(1) = \log(10^0) = 0 \times \log(10) = 0$

  1. $\log(1000) = \ldots $
Réponse

$\log (1000) \log (10^3) = 3 \times \log(10) = 3$

  1. $\log(\pu{0.01}) = \ldots $
Réponse

$\log(\pu{0.01}) = \log(10^{-2}) = -2 \times \log(10) = -2$

  1. Si $x$ est multiplié par 100, alors il faut …………………. …………….. au logarithme de $x$ pour trouver le logarithme du nouveau nombre ($100\, x$).
Réponse

Si $y = 100\, x$, $\log (y) = \log (100\, x) = \log(100) + \log (x) = \log(10^2) + \log(x) = 2 + \log (x)$. Il faut donc « ajouter 2 au $\ldots$ ».

  1. Si $x$ est multiplié par 100000, alors il faut …………………. …………….. au logarithme de $x$ pour trouver le logarithme du nouveau nombre ($100000\, x$).
Réponse

Si $y = 100000\, x$, $\log (y) = \log (100000\, x) = \log(100000) + \log (x) = \log(10^5) + \log(x) = 5 + \log (x)$. Il faut donc « ajouter 5 au $\ldots$ ».

  1. Si $x$ est divisé par 1000, alors il faut …………………. …………….. au logarithme de $x$ pour trouver le logarithme du nouveau nombre ($x/1000$).
Réponse

Si $y = \dfrac{x}{1000}$, $\log (y) = \log (\dfrac{x}{1000}) = \log (x) - \log(1000) = \log (x) - \log(10^3) = \log (x) - 3$. Il faut donc « retirer 3 au $\ldots$ ».

  1. Si $x$ est divisé par 10, alors il faut …………………. …………….. au logarithme de $x$ pour trouver le logarithme du nouveau nombre ($x/10$).
Réponse

Si $y = \dfrac{x}{10}$, $\log (y) = \log (\dfrac{x}{10}) = \log (x) - \log(10) = \log (x) - \log(10^1) = \log (x) - 1$. Il faut donc « retirer 1 au $\ldots$ ».

Application

On peut trouver très facilement une approximation, du nombre $\log(x)$ en utilisant, pour $x$ , la notation scientifique.

  1. Sachant que $\log(\pu{1,2}) = \pu{0,079}$, calculer, sans calculatrice, la valeur de $\log(120)$ : $\ldots$
Réponse

$\log (120) = \log (\pu{1,2e2}) = \log (\pu{1,2}) + \log (10^2) = \pu{0,079} + 2 = 2,079$.

  1. Sachant que $\log (\pu{3,14}) = \pu{0,497}$, calculer, sans calculatrice, la valeur de $\log(\pu{0,00314})$ : $\ldots$
Réponse

$\log (\pu{0,00314}) = \log (\pu{3,14e-3}) = \log (\pu{3,14}) + \log (10^{-3}) = \pu{0,497} -3 = -\pu{2,503}$.

Intensité sonore, niveau sonore

Intensité sonore

L’intensité sonore caractérise la puissance énergétique de l’onde en un point de l’espace, c’est à dire l’énergie que peut transmettre, chaque seconde, l’onde à un récepteur placé en ce point.
L’intensité sonore est donc une puissance surfacique et elle s’exprime en watt par mètre carré ($\pu{W/m2})$.

L’intensité sonore perceptible par l’oreille humaine est comprise entre une valeur minimale $I_0 = \pu{1,00e-12 W/m2}$ (seuil d’audition) et une valeur maximale (seuil de douleur) $I_{\text{max}} = \pu{25 W/m2}$.

Niveau d’intensité sonore

La sensation physiologique au niveau de l’oreille n’évolue pas proportionnellement à l’intensité sonore, car l’oreille n’est pas un récepteur linéaire.

Pour traduire correctement cette sensation physiologique, on définit donc une grandeur appelée niveau d’intensité sonore $L$ telle que : $$ L = 10 \log \left( \dfrac{I}{I_0} \right) $$ avec $I_0 = \pu{1,00e-12 W/m2}$. L’unité de $L$ est le décibel, de symbole $\pu{dB}$.

Le niveau sonore présente donc deux particularités :

  • Il est relatif à la sensibilité de l’oreille humaine ;
  • Son évolution est logarithmique.
  1. Si $I$ est multipliée par 100, alors le niveau sonore …………………. …………….. dB.
Réponse

Si $I’ = 100\, I$, $L’ = 10 \log \left( \dfrac{100\, I}{I_0} \right) = 10 \log (100) + 10 \log \left( \dfrac{I}{I_0} \right) = 20 + L$. Le niveau sonore augmente donc de $\pu{20 dB}$.

  1. Si $I$ est multipliée par 2, alors le niveau sonore …………………. …………….. dB.
Réponse

Si $I’ = 2\, I$, $L’ = 10 \log \left( \dfrac{2\, I}{I_0} \right) = 10 \log (2) + 10 \log \left( \dfrac{I}{I_0} \right) = 3,0 + L$. Le niveau sonore augmente donc de $\pu{3,0 dB}$.

  1. Au bord d’une voie ferrée, on mesure un niveau d’intensité sonore égal à $\pu{100 dB}$ au passage d’un train. Quelle est l’intensité sonore correspondante ?
Réponse

$L = 10 \log \left( \dfrac{I}{I_0} \right) \Harr I = I_0 \times 10^{L/10}$.
A.N. $ I = \pu{1,00e-12 W/m2} \times 10^{100/10} = \pu{1,00e-2 W/m2}$.

Les intensités sonores s’ajoutent mais pas les niveaux sonores !

Atténuation de l’intensité d’une onde sonore

Dans le cas d’une onde à la surface de l’eau, l’énergie fournie par la source se répartit sur des rides circulaires de rayon croissant. La hauteur des ondulations diminue progressivement.
Cette atténuation de l’amplitude de la perturbation existe, dans les milieux à deux ou trois dimensions, alors que l’énergie transportée par la perturbation peut rester constante.

Dans un milieu non absorbant

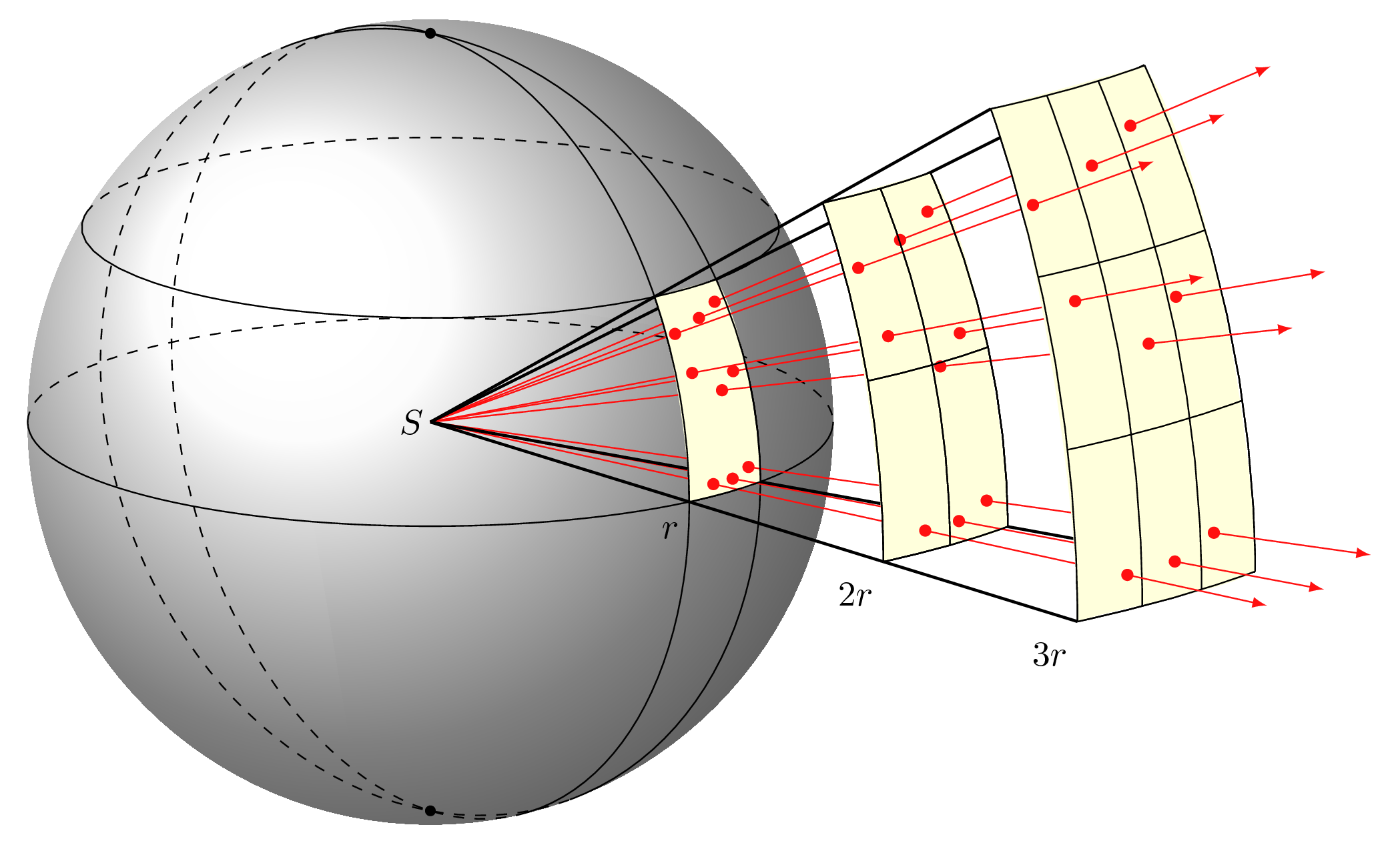
L’atténuation d’une onde n’est pas forcément due à une absorption de l’énergie par le milieu dans lequel l’onde se propage. Au fur et à mesure de la propagation, l’énergie fournie par la source se répartit sur un front d’onde de plus en plus grand. L’énergie reçue en chaque point de chacun de ces fronts d’onde diminue donc et l’amplitude de l’onde diminue ; on parle d’atténuation géométrique.

Dans un milieu absorbant

Lorsqu’une onde sonore se propage dans un milieu absorbant, une partie de l’énergie est transférée au milieu. Ainsi, l’intensité sonore décroît entre l’entrée de l’onde dans le milieu et sa sortie. Cette atténuation s’ajoute à l’atténuation géométrique.

Lorsqu’une onde sonore se propage dans un milieu absorbant, on définit l’attténuation de l’onde par : $$ A = L_{\text{sortie}} - L_{\text{entrée}} = 10\, \log \left( \dfrac{I_{\text{sortie}}}{I_{\text{entrée}}} \right) $$ avec $L_{\text{sortie}}$ le niveau d’intensité sonore en sortie (dB), $L_{\text{entrée}}$ le niveau d’intensité sonore en entrée (dB), $I_{\text{sortie}}$ l’intensité sonore en sortie ($\pu{W.m^{-2}}$) et $I_{\text{entrée}}$ l’intensité sonore en entrée ($\pu{W.m^{-2}}$).

Entraînement

Le son d’un diapason

Un son pur est un son qui ne possède pas d’harmonique, c’est à dire une onde sinusoïdale. Un diapason émet un son pur de fréquence $f = \pu{880 Hz}$.

Donnée :
vitesse du son dans l’air à $\pu{20 °C}$, $v_{\text{son}} = \pu{340 m/s}$.
  1. Quelle est la longueur d’onde $\lambda_{\text{air}}$ de ce son dans l’air ?
  2. Au bout de quelle durée ce son est-il perçu par une personne située à $\pu{10 m}$ du diapason ?
  3. L’intensité sonore perçue par cette personne vaut $\pu{1,0e-10 W/m2}$. Quel est le niveau d’intensité sonore $L$ correspondant ?
  4. Quel serait le niveau d’intensité sonore pour cette personne si trois diapasons émettaient simultanément un son de même intensité ?
Réponses

  1. La longueur d’onde d’une onde sinusoïdale est la distance parcourue par cette onde pendant la durée $T$, donc $\lambda_{\text{son}} = v_{\text{son}} \cdot T_{\text{son}}$. Comme $T = \dfrac{1}{f}$, $\lambda_{\text{son}} = \dfrac{v_{\text{son}}}{f_{\text{son}}}$. A.N. $\lambda_{\text{son}} = \dfrac{\pu{340 m/s}}{\pu{880 Hz}} = \pu{3,86e-1 m}$.

  2. L’onde parvient au niveau avec un certain retard $\tau$ : durée nécessaire à la propagation du signal, $\tau = \dfrac{d}{v_{\text{son}}}$. A.N. $\tau = \dfrac{\pu{10 m}}{\pu{340 m/s}} = \pu{2,9e-2 s} = \pu{29 ms}$.

  3. A.N. $L = 10 \log \left( \dfrac{\pu{1,0e-10 W/m2}}{\pu{1,00e-12 W/m2}} \right) = \pu{20 dB}$.

  4. Les intensités sonores s’ajoutent mais pas les niveaux sonores !
    Si $I’ = 3\, I$, $L’ = 10 \log \left( \dfrac{3\, I}{I_0} \right) = 10 \log (3) + 10 \log \left( \dfrac{I}{I_0} \right) = \pu{4,78 dB} + \pu{20 dB} = \pu{25 dB}$.

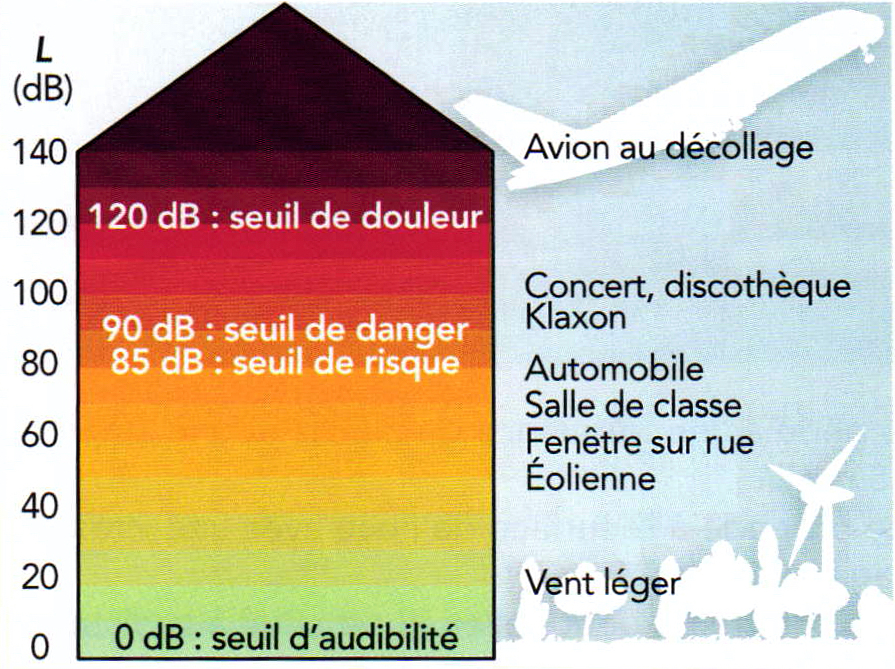
L’oreille humaine en concert

Pour régler le niveau sonore de la salle de concert, un ingénieur du son connaît certaines règles. Par exemple, s’il fait ses réglages pour avoir un son de $\pu{98 dB}$ pour des spectateurs situés à $\pu{16 m}$ d’une enceinte, il sait que l’intensité sonore sera quatre fois plus grande pour les spectateurs situés à $\pu{8 m}$ de l’enceinte. Il sait aussi que l’intensité sonore est doublée s’il place côte à côte deux enceintes identiques. Pour ces réglages cet ingénieur doit tenir compte des seuils de risque, de danger et de douleur. En effet l’exposition à un niveau sonore trop élevé peut provoquer des acouphènes. L’acouphène est un bourdonnement ou sifflement parasite qu’une personne entend sans que ce bruit existe réellement.

  1. Montrer que l’intensité $I_1$, du son à 16 mètres de l’enceinte vaut $I_1 = \pu{6.3e-3 W/m2}$.
  2. Si l’ingénieur place dix enceintes identiques côte à côte sur la scène, quel est le niveau d’intensité sonore $L_2$ à $\pu{16 m}$ ?
  3. Montrer que le niveau d’intensité sonore augmente de $\pu{6 dB}$ chaque fois que l’on divise la distance par deux.
  4. À partir de quelle distance des enceintes le son est-il douloureux à écouter ?
Réponses

  1. $L_1 = 10 \log \left( \dfrac{I_1}{I_0} \right) \Harr I_1 = I_0\, 10^{L_1/10}$.
    A.N. $ I_1 = \pu{1,00e-12 W/m2} \times 10^{98/10} = \pu{6,3e-3 W/m2}$.

  2. Les intensités sonores s’ajoutent mais pas les niveaux sonores !
    Si $I_2 = 10\, I_1$, $L_2 = 10 \log \left( \dfrac{10\, I_1}{I_0} \right) = 10 \log (10) + 10 \log \left( \dfrac{I_1}{I_0} \right) = \pu{10 dB} + L_1 = \pu{10 dB} + \pu{98 dB} = \pu{108 dB}$.

  3. L’énergie émise par la source se répartit sur des fronts d’onde qu’on suppose sphériques, donc si on note $P_0$ la puissance sonore de la source, à la distance $r_1$, l’intensité sonore $I_1$, qui est la puissance surfacique, est égale à $\dfrac{P_0}{S_1}$ où $S_1$ est la surface de ce front d’onde. Comme $S_1 = 4\pi r_1^2$, $I_1 = \dfrac{P_0}{4 \pi r_1^2}$. De même, à la distance $r_2$, l’intensité sonore a pour expression : $I_2 = \dfrac{P_0}{4 \pi r_2^2}$. On en déduit donc que $P_0 = 4 \pi r_1^2\, I_1 = 4 \pi r_2^2\, I_2$ ou $\dfrac{I_1}{I_2} = \dfrac{r_2^2}{r_1^2}$.
    Si $r_1 = 2 r_2$, $\dfrac{I_1}{I_2} = \dfrac{r_2^2}{4 r_2^2} = \dfrac{1}{4}$ ou $I_2 = 4\, I_1$. Lorsqu’on divise la distance par 2 l’intensité sonore est multipliée par 4.
    $L_2 = 10 \log \left( \dfrac{I_2}{I_0} \right) = 10 \log \left( \dfrac{4\, I_1}{I_0} \right) = 10 \log(4) + L_1 = \pu{6,0 dB} + L_1$. Lorsqu’on divise la distance par 2 l’intensité sonore est multipliée par 4 et le niveau d’intensité sonore est augmenté de $\pu{6,0 dB}$.

  4. À $d=\pu{16,0 m}$, on a calculé que le niveau sonore est égal à $L_2 = \pu{108 dB}$. De plus, à la question précédente, on a démontré que chaque fois qu’on divise la distance la distance par 2, le niveau sonore augmente de $\pu{6,0 dB}$, donc à $\pu{8,0 m}$ le niveau sonore vaut $\pu{108 dB} + \pu{6,0 dB} = \pu{114 dB}$ et à $\pu{4,0 m}$ le niveau sonore vaut $\pu{114 dB} + \pu{6,0 dB} = \pu{120 dB}$. C’est le seuil de douleur ; personne ne doit donc se rapprocher à moins de $\pu{4,0 m}$ des enceintes.

Autre démonstration : puisque $\dfrac{I_1}{I_2} = \dfrac{r_2^2}{r_1^2}$, $I_2 = I_1 \, \left( \dfrac{r_1}{r_2} \right)^2$ et $L_2 = 10 \log \left( \dfrac{I_2}{I_0} \right) = 10 \log \left( \dfrac{I_1 \, \left( \dfrac{r_1}{r_2} \right)^2}{I_0} \right) = 10 \log \left( \dfrac{I_1}{I_0} \right) + 20 \log \left( \dfrac{r_1}{r_2} \right)$.

Finalement $ L_2 = L_1 + 20 \log \left( \dfrac{r_1}{r_2} \right) \Leftrightarrow r_2 = r_1 \times 10^{\frac{-(L_2 - L_1)}{20}}$.

A.N. $r_2 = \pu{16,0 m} \times 10^{\frac{-(120 - 108)}{20}} = \pu{4,0 m}$.

Casque anti-bruit

Sur un chantier de travaux publics, un ouvrier est placé à une distance $d=\pu{1,0 m}$ d’un engin émettant un bruit dont la puissance sonore est $P=\pu{15 mW}$.

Données

  • Expression de l’atténuation géométrique : $I = \dfrac{P}{4\pi\, d^2}$ ;
  • Seuil de danger pour le système auditif : $L_{\text{danger}} = \pu{85 dB}$.

  1. Vérifier si le bruit perçu par cet ouvrier présente un danger pour son système auditif.

  2. L’ouvrier met un casque anti-bruit dont l’atténuation est de $\pu{−20 dB}$. Préciser si le danger persiste.

  3. L’ouvrier retire son casque et s’éloigne pour se positionner à 10 m de l’engin. Conclure quant à la dangerosité de cette exposition au bruit.

Réponses
Intensité sonore  Ondes  Logarithme  Niveau sonore 

Suggestions de lecture :