Caractéristiques des ondes mécaniques progressives

Qu’est ce qu’une onde progressive ?

Étude de quelques simulations de propagation d’ondes mécaniques

Onde progressive se propageant le long d'une corde

Onde mécanique progressive

Une perturbation/déformation correspond à la modification d’une propriété mécanique (vitesse, position, …) des constituants d’un milieu matériel.

On appelle onde mécanique progressive le phénomène de propagation d’une perturbation dans un milieu matériel, de proche en proche, sans transport de matière mais avec transport d’énergie.

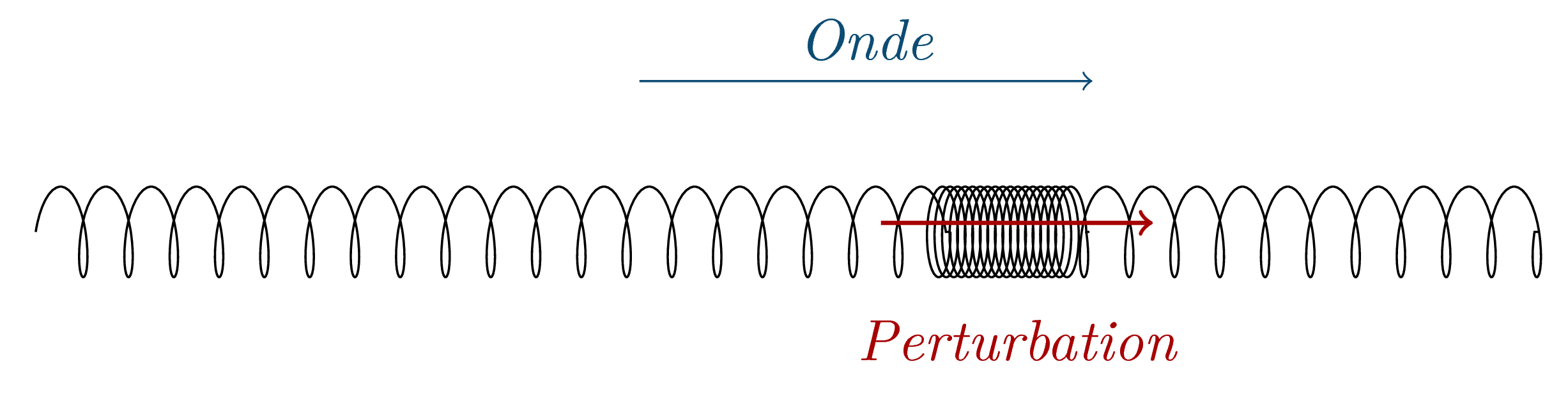
Onde progressive longitudinale

Une onde progressive est dite longitudinale lorsqu’elle se propage selon une direction parallèle à la direction de la déformation. Onde longitudinale le long d'un ressort

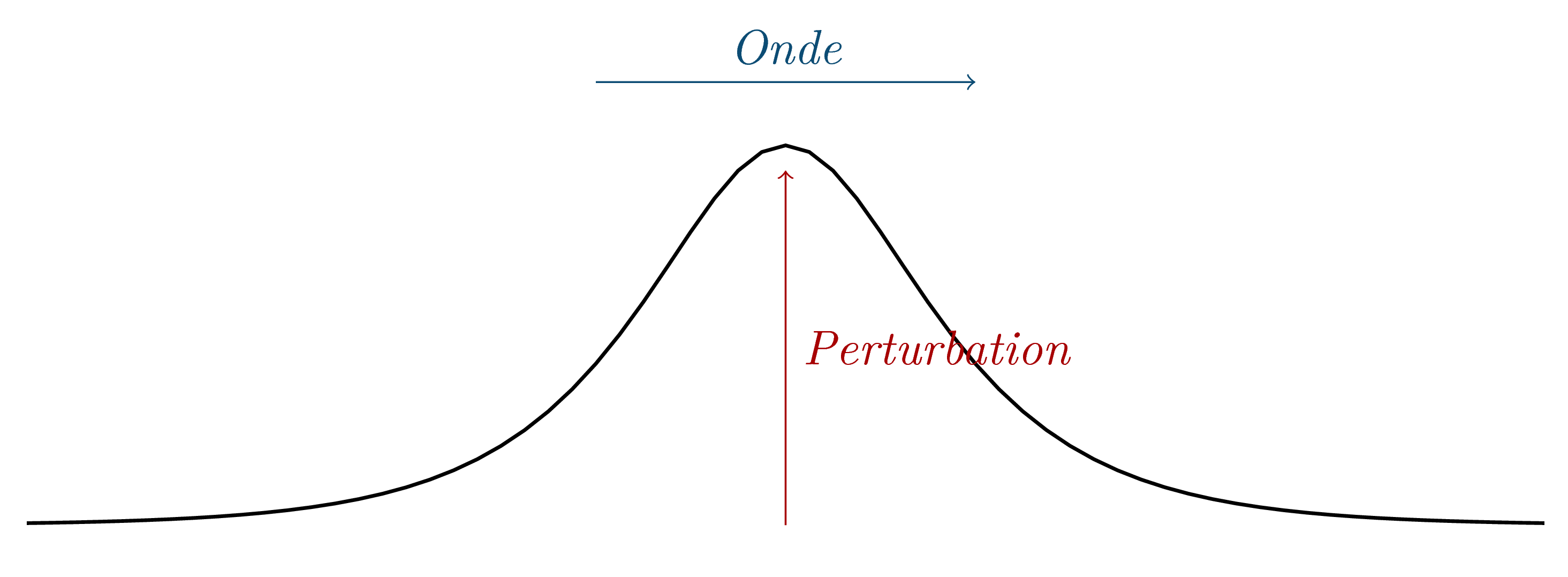
Onde progressive transversale

Une onde progressive est dite transversale (ou transverse) lorsqu’elle se propage selon une direction perpendiculaire à la direction de la déformation. Onde transverale le long d'une corde

Une onde mécanique se transmet de proche en proche

Une onde mécanique se propage de « proche en proche », chaque point du milieu reproduit le mouvement de son voisin immédiat avec un léger retard.

Une onde mécanique se propage sans transport de matière

Chaque point du milieu dans lequel se propage l’onde reprend sa position initiale après le passage de l’onde.

Transport d’énergie

Une onde transporte l’énergie fournie par la source de proche en proche.

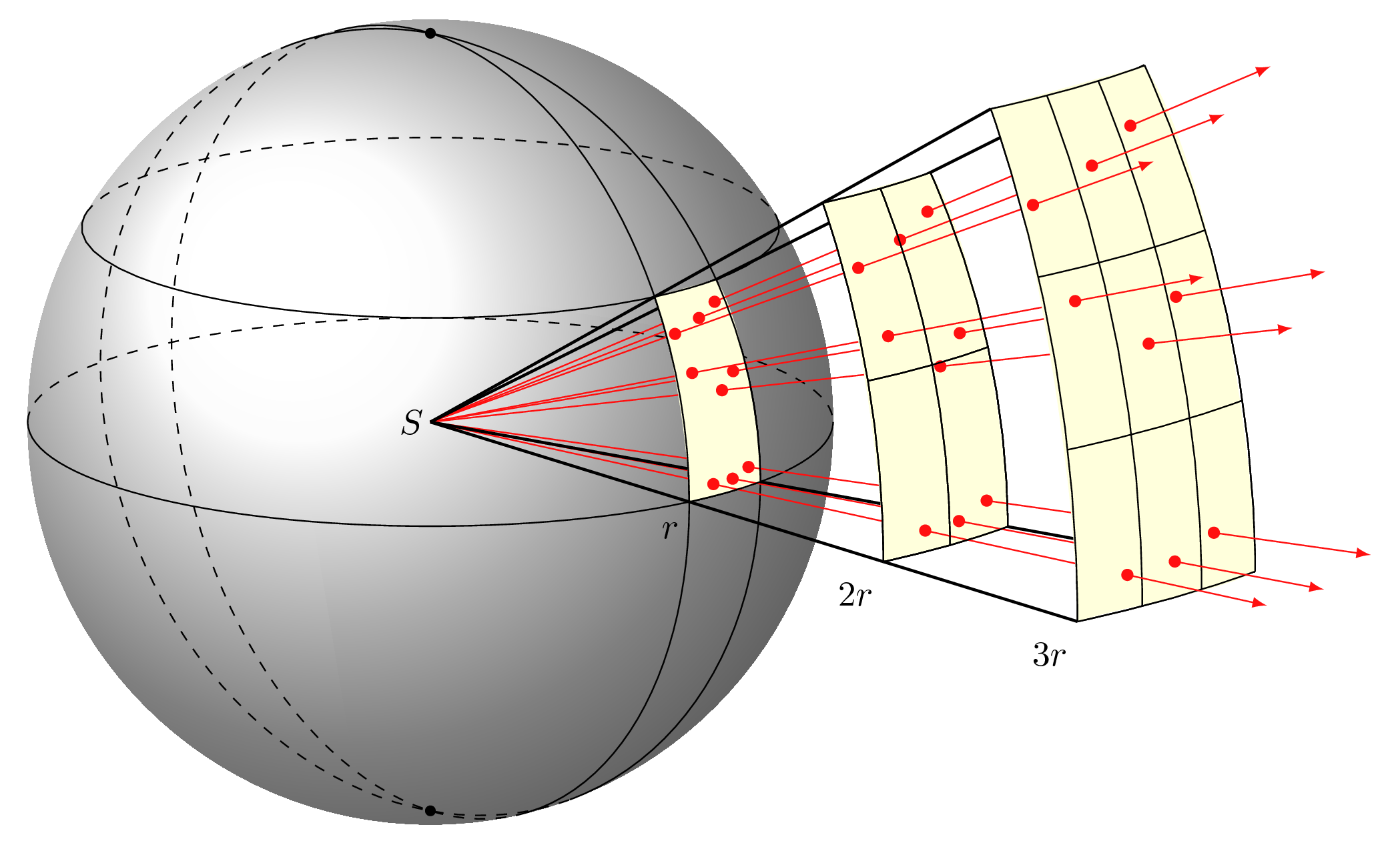
Atténuation d’une onde

Dans le cas d’une onde à la surface de l’eau, l’énergie fournie par la source se répartit sur des rides circulaires de rayon croissant. La hauteur des ondulations diminue progressivement.
Cette atténuation de l’amplitude de la perturbation existe, dans les milieux à deux ou trois dimensions, alors que l’énergie transportée par la perturbation peut rester constante.

L’atténuation d’une onde n’est pas forcément due à une absorption de l’énergie par le milieu dans lequel l’onde se propage. Au fur et à mesure de la propagation, l’énergie fournie par la source se répartit sur un front d’onde de plus en plus grand. L’énergie reçue en chaque point de chacun de ces fronts d’onde diminue donc et l’amplitude de l’onde diminue.

Remarques

Seules les ondes progressives longitudinales se propagent dans les fluides.
Les solides transmettent les ondes progressives longitudinales et transversales.
Les ondes mécaniques nécessitent la présence d’un milieu et ne peuvent donc pas se propager dans le vide.

Célérité d’une onde

Pour bien souligner que les caractéristiques d’une onde ne sont pas celles d’un objet matériel, on appelle célérité la vitesse de déplacement de la déformation d’un milieu. C’est aussi la vitesse de déplacement de l’énergie.

De quoi dépend la célérité d’une onde ?

La célérité d’une onde qui se propage dans un milieu non dispersif est caractéristique de ce milieu.
La célérité d’une onde progressive ne dépend pas (sauf cas particulier) de la valeur de l’élongation (importance de la déformation) de cette onde.

Remarques

Plus le milieu est rigide, plus la célérité est grande.
- Sur une corde, la célérité d’une onde est d’autant plus grande que la corde est tendue.
- La célérité du son est plus grande dans un solide que dans l’eau et elle est plus grande dans l’eau que dans l’air.
Plus l’inertie du milieu est grande, plus la célérité diminue.
- Sur une corde, la célérité est d’autant plus grande que la masse linéique est faible.
- Sur une échelle de perroquet, la célérité est d’autant plus petite que la longueur des barreaux est grande.

Notion de retard

Retard d’une onde

Dans un milieu non absorbant et non dispersif, chaque point de l’espace atteint par une onde progressive reproduit exactement le mouvement de la source un peu plus tard dans le temps.
On appelle retard la durée nécessaire à la propagation de l’onde entre deux points étudiés.

Expression du retard

- Le retard avec lequel l'onde atteint le point d'abscisse $x_2$ est, si on note $v$ la célérité de l'onde : $$ \tau = \dfrac{x_2 - x_1}{v}$$ - La la date $t_2$ à laquelle l'onde atteint cette abscisse est alors : $$ t_2 = t_1 + \tau$$

Qu’est-ce qu’une onde progressive périodique ?

Phénomène périodique

Un phénomène est dit périodique (dans le temps) s’il se reproduit identique à lui-même à intervalles de temps égaux.

> Fig. 1 — Mouvement dans le temps d'une source $S$ (à la position $x=0$, par exemple). Bien remarquer que l'axe des abscisses représente le temps.

Remarque

Un phénomène périodique n’a ni début ni fin ; c’est un modèle.

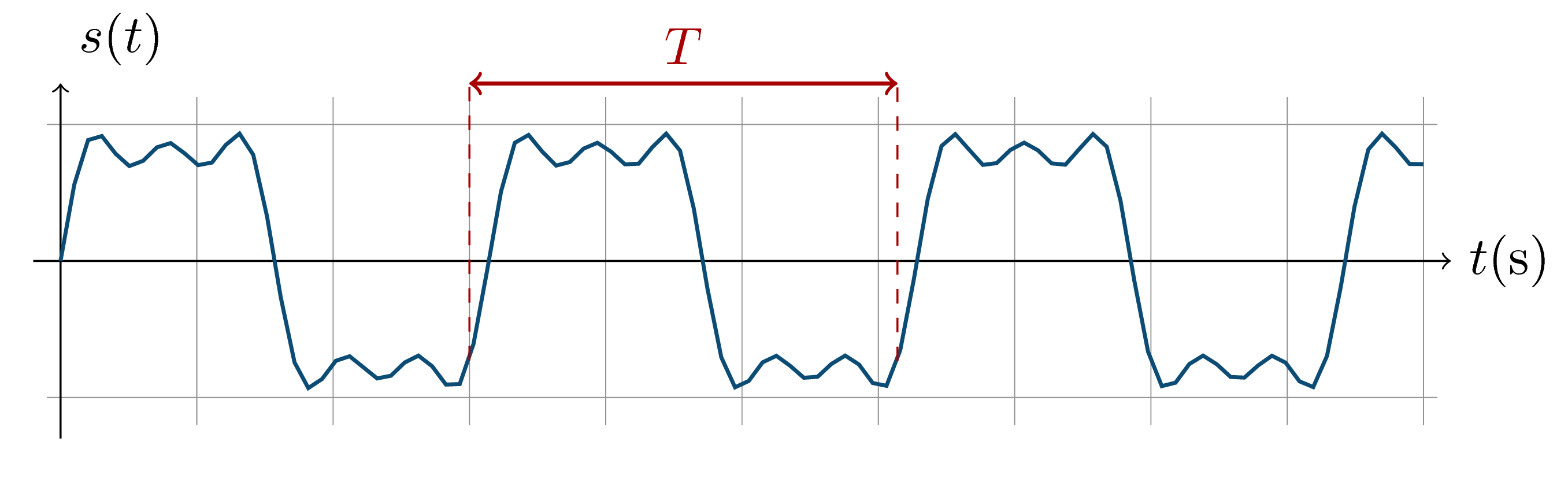La période (temporelle) $T$ d’un phénomène périodique est la plus petite durée au bout de laquelle ce phénomène se reproduit identique à lui-même.

> Fig. 2 — Période $T$ d'un phénomène périodique. Bien remarquer que l'axe des abscisses représente le temps.

Le fréquence $f$ d’un phénomène périodique est le nombre de fois que ce phénomène se reproduit identique à lui-même pendant la durée d’une seconde.
La fréquence $f$ est donc aussi égale au nombre de périodes $T$ du phénomène périodique durant une seconde : $$f = \dfrac{1}{T}$$ avec $f$ en hertz (Hz) et $T$ en seconde (s).

Remarque

$$\pu{1 Hz} = \pu{1 s-1}$$

Périodicité temporelle d’une onde progressive périodique

Chaque point matériel atteint par l’onde reproduisant le mouvement de la source avec un certain retard, si la source possède un mouvement périodique dans le temps, chaque point possède le même mouvement périodique mais décalé dans le temps.
La période (temporelle) de chaque point du milieu est identique à celle de la source (propriété de linéarité du milieu).
La période temporelle d’une onde progressive est identique à celle de la source qui lui donne naissance.

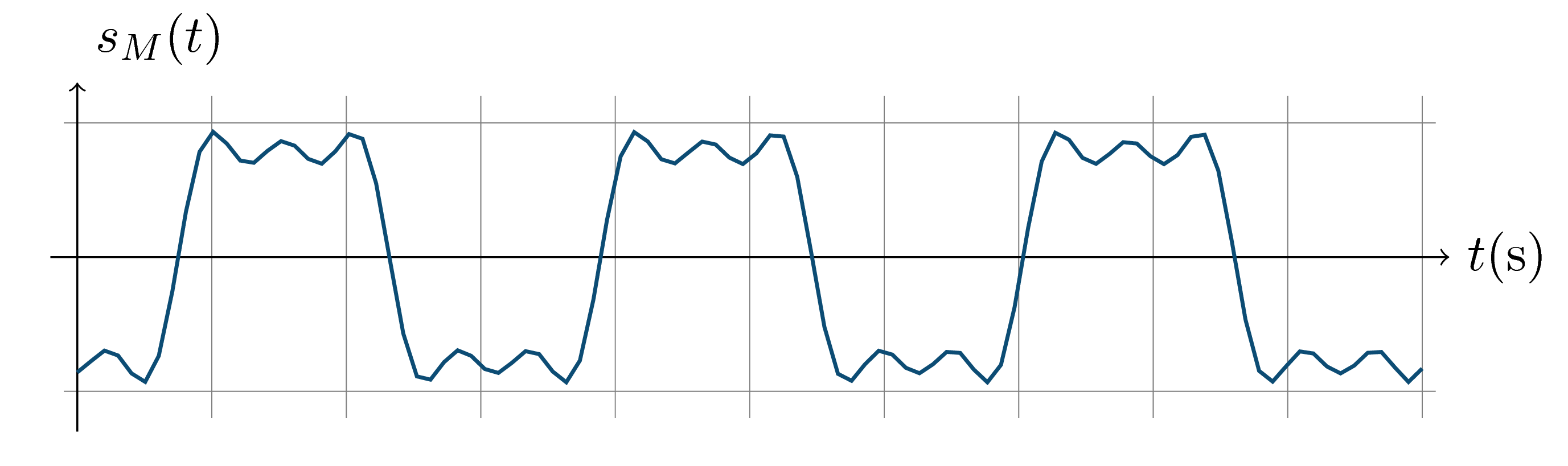> Fig. 3 — Mouvement dans le temps d'un point quelconque $M$ atteint par l'onde (à la position $x=a$ par exemple). Noter le **déphasage** par rapport au mouvement de la source (en $x=0$), sur la figure 1. Bien remarquer que l'axe des abscisses représente le temps.

Comment déterminer la période temporelle d’une onde ?

Rester immobile, ce qui revient à fixer les coordonnées d’espace, et laisser s’écouler le temps.

Périodicité spatiale d’une onde progressive périodique

Déphasage entre le mouvement de deux points distincts

Deux points matériels situés à des distances différentes de la source, atteints par une onde progressive, le sont avec des retards différents. Les mouvements dans le temps de ces deux points sont déphasés — les valeurs des élongations de l’onde en chacun des points sont différentes.

Période spatiale

Lorsqu’on prend une photo instantanée du milieu, l’image obtenue présente un motif (spatial) qui se répète, identique à lui-même. On dit que l’onde progressive périodique présente une périodicité spatiale.

Remarques

C’est le déphasage entre tous les points que l’onde périodique atteint qui est à l’origine de la périodicité spatiale.
La périodicité spatiale d’une onde périodique non sinusoïdale (cf. section suivante) ne porte aucun nom.

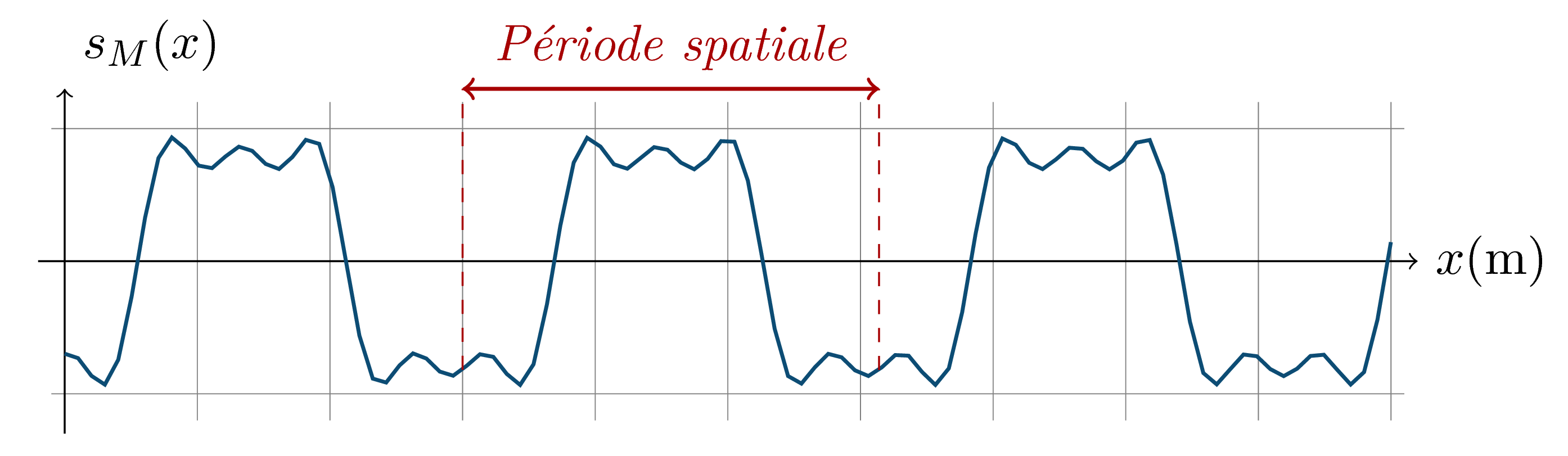> Fig. 4 — Cartographie de l'espace à une date quelconque. Bien remarquer que l'**axe des abscisses représente l'espace**. La période spatiale s'exprime en mètre (m).

Comment déterminer la période spatiale d’une onde ?

Prendre une photo instantanée du milieu, ce qui revient à fixer les coordonnées de temps, et explorer l’espace.

Qu’est-ce qu’une onde progressive sinusoïdale ?

Onde progressive sinusoïdale

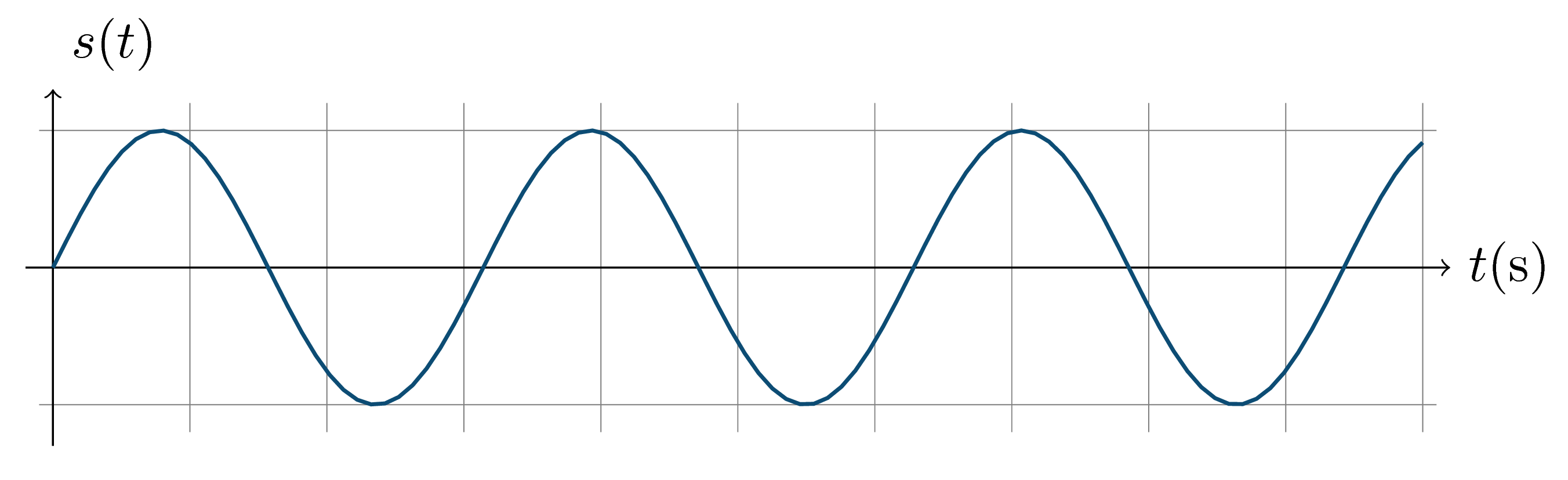Une onde progressive sinusoïdale est une onde progressive périodique créée par une source possédant un mouvement périodique sinusoïdal (dans le temps), de période $T$.

> Fig. 5 — Mouvement sinusoïdal d'une source $S$ (à la position $x=0$ par exemple).

Puisque chaque point matériel atteint par l’onde reproduit le mouvement de la source avec un certain retard, si cette dernière possède un mouvement sinusoïdal dans le temps, ces points possèdent le même mouvement sinusoïdal, déphasé dans le temps.
La période (temporelle) des mouvements de ces points est identique à celle de la source.

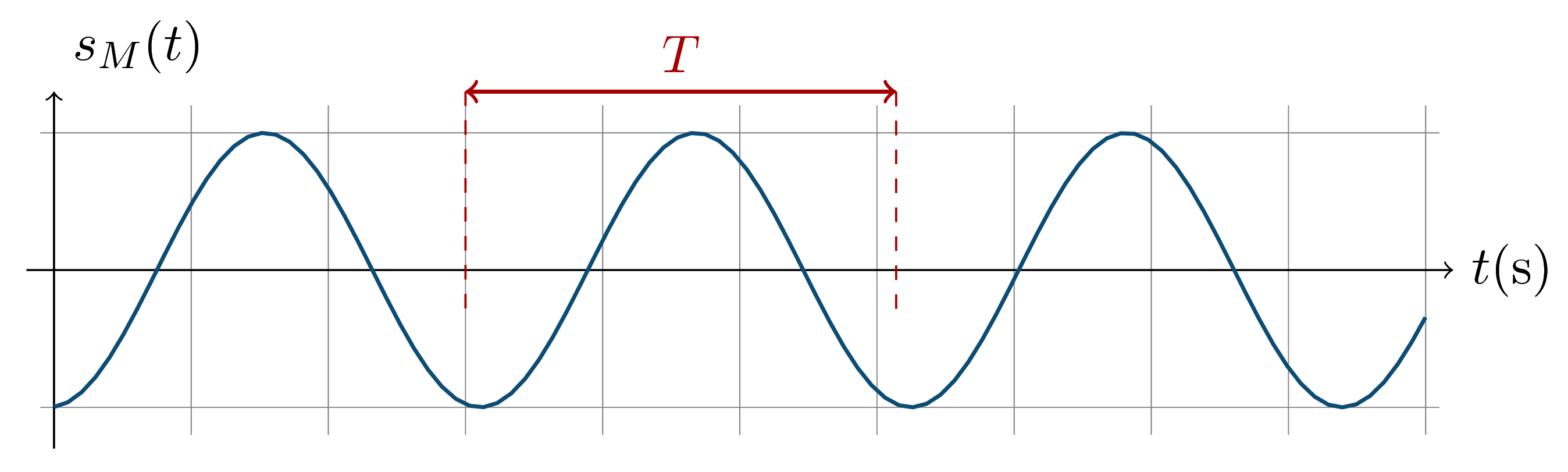> Fig. 6 — Mouvement dans le temps d'un point quelconque $M$ atteint par l'onde (à la position $x=a$ par exemple). Noter le déphasage par rapport au mouvement de la source (en $x=0$) sur la figure 5. Bien remarquer que l'**axe des abscisses représente le temps**.

Longueur d’onde

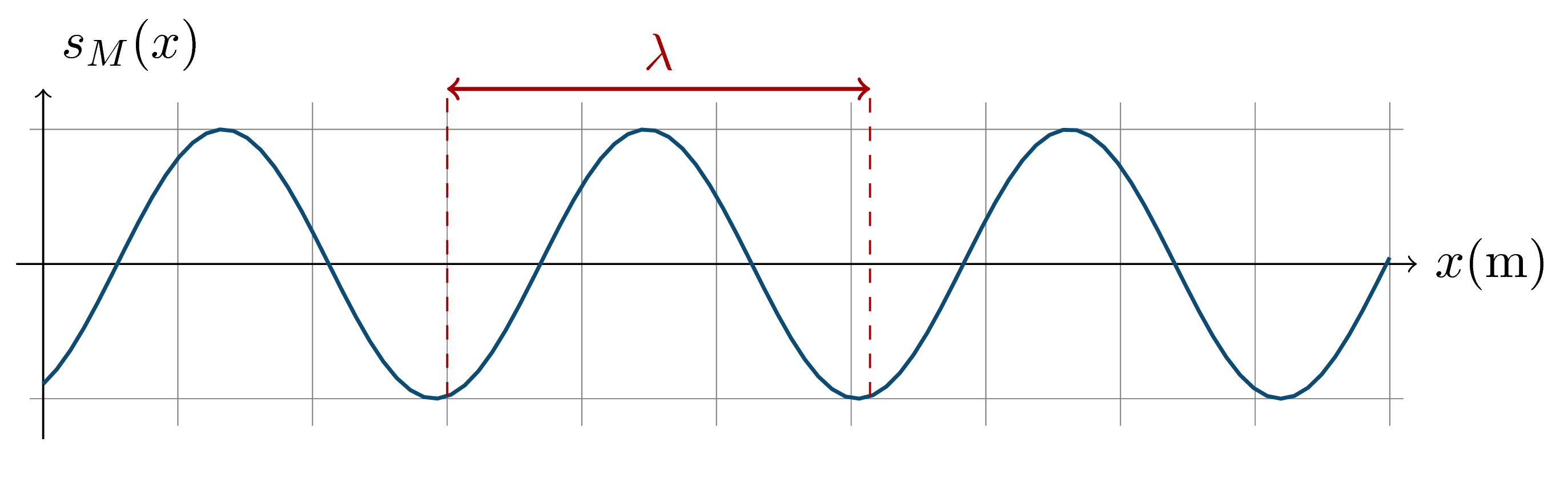On appelle longueur d’onde la période spatiale d’une onde progressive sinusoïdale. La longueur d’onde se note $\lambda$ et s’exprime en mètre (m).

> Cartographie de l'espace à une date quelconque. Bien remarquer que l'**axe des abscisses représente l'espace**.

Relation entre la longueur d’onde et la période temporelle

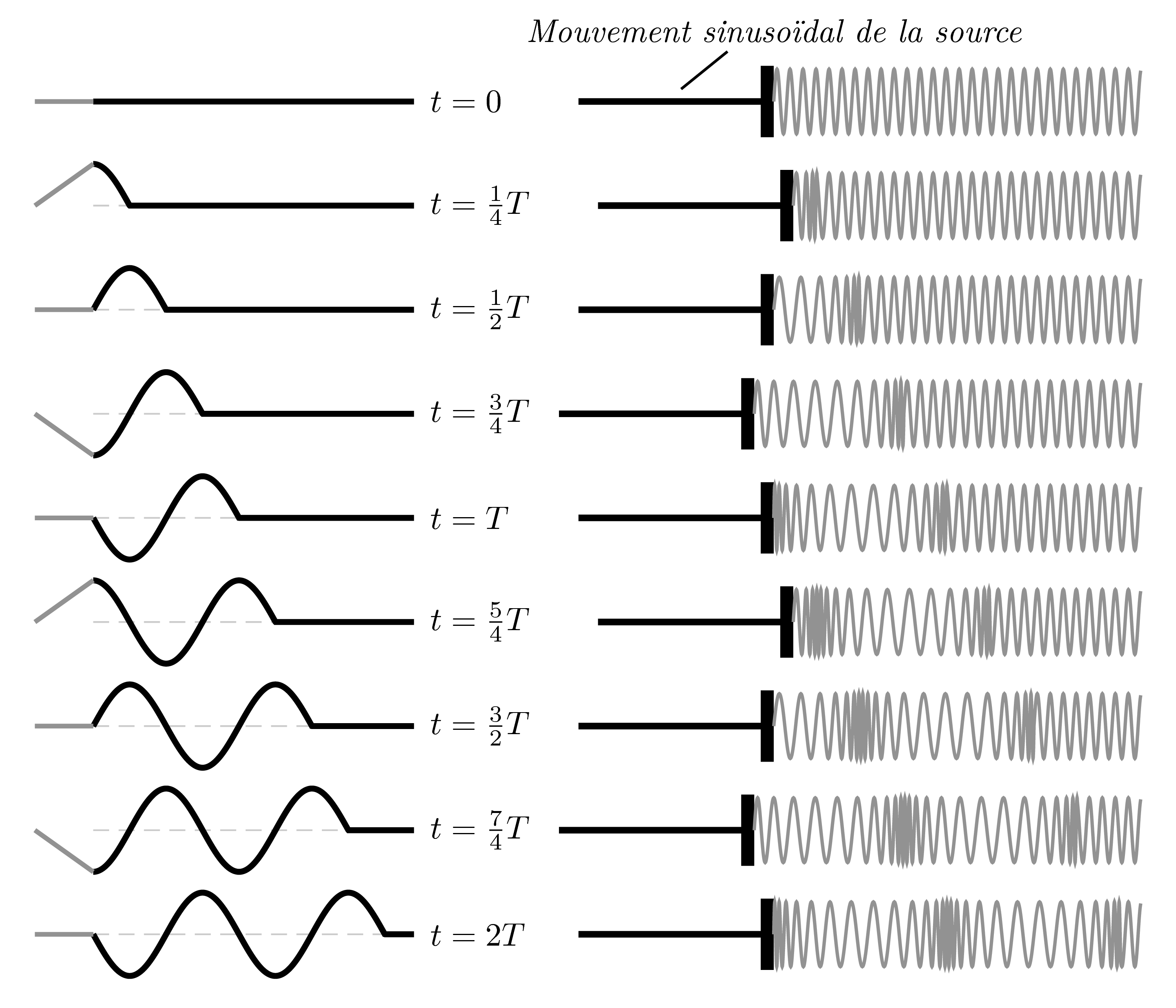> Allures d'une corde et d'une tranche d'air (ou d'un ressort) à différentes dates. La signification de la longueur d'onde apparaît clairement : c'est la distance parcourue par l'onde pendant la durée $T$ à la vitesse $v$.

La longueur d’onde $lambda$ d’une onde sinusoïdale est la distance parcourue par l’onde pendant une durée égale à sa période temporelle $T$ à la vitesse $v$.
Donc $$\lambda = v\, T$$