Rappels d'algorithmique

Algorithmique

Un algorithme est une suite finie et non ambiguë d’opérations ou d’instructions à réaliser afin de résoudre un problème.

En informatique, pour qu’un algorithme puisse être implémenté, il est nécessaire de s’assurer que la « suite finie et non ambiguë d’opérations ou d’instructions à réaliser » s’effectue en une durée finie .

Lorsqu’on élabore ou étudie un algorithme, il est donc nécessaire de vérifier :

  • Sa finitude : Il doit se terminer en un temps fini.
  • Sa correction : Il doit (généralement) donner le bon résultat.
  • Sa performance : Plusieurs algorithmes peuvent permettre de résoudre une même classe de problèmes. Ils ne nécessiteront cependant pas tous l’utilisation de la même quantité de mémoire ou le même nombre d’étapes de calcul, donc la même durée.

Remarques

  • Ce n’est pas toujours une mauvaise nouvelle si certains algorithmes ont besoin d’un « temps infini » pour résoudre un problème : certains choix en cryptographie reposent sur l’idée que « casser » la protection nécessite une durée de calcul trop grande, pour le matériel dont on dispose aujourd’hui.
  • Pour certains problèmes on doit se contenter d’une solution approchée et pas d’une solution exacte.
La performance d’un algorithme porte sur deux aspects : la durée du calcul et la quantité de mémoire nécessaires à la résolution du problème. Malheureusement ces deux points s’opposent . Il est souvent nécessaire d’occuper davantage de mémoire pour gagner en temps de calcul, ou d’écrire plus d’instructions, et donc faire plus de calculs, pour aboutir à une gestion de la mémoire optimale.

Conformément au programme, on limite la performance algorithmique à la complexité algorithmique.

Notion de complexité algorithmique

Introduction

La complexité algorithmique donne des informations sur la durée du calcul nécessaire à la résolution du problème. Plus la complexité algorithmique est petite, moins de calculs sont effectués et plus l’algorithme est performant (sous réserve que la gestion de l’espace mémoire utilisé par l’implémentation de l’algorithme ne constitue pas un problème).
On exprime la complexité d’un algorithme en fonction de la taille (nombre) des données qu’il manipule en considérant que chaque instruction élémentaire s’effectue en temps constant.

Il existe plusieurs méthodes pour analyser la complexité d’un algorithme, comme :

  • L’analyse moyenne : Il s’agit d’évaluer comment varie la durée moyenne des calculs à effectuer en fonction du nombre de données manipulées.

  • L’analyse optimiste Il s’agit d’évaluer comment varie le nombre de calculs à effectuer, dans le scénario le plus favorable, en fonction du nombre de données manipulées.
    Par exemple, on cherche une valeur dans une liste et c’est la première qui apparaît lors de cette recherche.

  • L’analyse pessimiste (ou du pire cas) : Il s’agit d’évaluer comment varie le nombre de calculs à effectuer, dans le scénario le moins favorable, en fonction du nombre de données manipulées. Par exemple, on cherche une valeur dans une liste alors qu’elle n’est pas présente dans la liste.

Lorsqu’on utilise le résultat de l’analyse du « pire cas », aucune mauvaise surprise ne peut intervenir, le pire cas à été envisagé à l’avance.

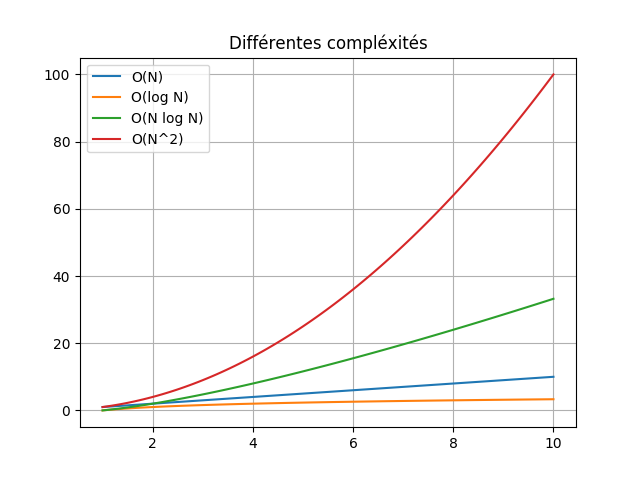
Les complexités des différents algorithmes varient beaucoup. On peut néanmoins regrouper les algorithmes en quelques grandes familles :

  • Complexité constante : Leur notation est de la forme $O(1)$. Ces algorithmes sont indépendants du nombre de données à traiter.
La complexité constante apparaît dans la recherche par index dans un tableau.
La complexité constante est la plus « performante ».
  • Les algorithmes logarithmiques : Leur notation est de la forme $O(\log N)$. Ces algorithmes sont très performants en temps de traitement. Le nombre de calculs dépend du logarithme du nombre de données à traiter.
    Sur la Figure ci-dessous, on peut constater que, plus le nombre de données $N$ à traiter est important, moins le nombre de calcul à effectuer augmente rapidement — la valeur de la dérivée est de moins en moins grande.
    La fonction logarithme à utiliser dépend du problème étudié mais, comme la complexité est définie à un facteur près, la base du logarithme n’a pas d’importance.
La complexité logarithmique apparaît dans les problèmes dans lesquels l’ensemble des données peut être décomposé en deux parties égales, qui sont elles-mêmes décomposées en 2 (recherche par dichotomie, recherche dans un arbre binaire, etc.).
La complexité logarithmique est très « performante ».
Le logarithme à utiliser est alors la fonction réciproque de $f : x \longmapsto 2^x$, c’est à dire $\log_{2}$ (aussi appelé logarithme entier).
Le logarithme entier d’un nombre $x$ supérieur ou égal à 1 est le nombre de fois qu’il faut le diviser par deux pour obtenir un nombre inférieur ou égal à 1.
  • Les algorithmes linéaires : Leur notation est de la forme $O(N)$. Ces algorithmes sont rapides. Le nombre de calculs dépend, de manière linéaire, du nombre de données initiales à traiter.
La complexité linéaire apparaît dans les problèmes dans lesquels on parcourt séquentiellement l’ensemble des données pour réaliser une opération (recherche d’une valeur, par exemple).
La complexité linéaire est considérée comme « efficace ».
  • Les algorithmes linéaires et logarithmiques (quasi-linéaire) : Leur notation est de la forme $O(N \log N)$.
La complexité linéaire et logarithmique apparaît dans des problèmes dans lesquels on découpe répétitivement les données en deux parties, que l’on parcourt séquentiellement ensuite (tri Quicksort par exemple).
La complexité quasi-linéaire est considérée comme « assez efficace ».
  • Les algorithmes de type polynomiale : Leur notation est de la forme $O(N^k)$ où $k$ est la puissance.
Une complexité quadratique apparaît, par exemple, lorsqu’on parcourt un tableau à deux dimensions, lorsqu’on effectue un tri par comparaison, etc.
La complexité polynomiale est considérée comme « moyennement efficace ».
  • Les algorithmes exponentiels ou factoriels : Leur notation est de la forme $O(e^N)$ ou $O(N!)$. Ce sont les algorithmes les plus complexes.
    Le nombre de calculs augmente de façon exponentielle ou factorielle en fonction du nombre de données à traiter. Un algorithme de complexité exponentielle traitera, dans le pire des cas, un ensemble de 10 données en effectuant 22026 calculs ; un ensemble de 100 données en effectuant $\pu{2,688e43}$ calculs !!! On dit généralement que les problèmes produisant ce type d’algorithmes sont « non calculables ».
On rencontre les algorithmes de type exponentiels ou factoriels dans les problématiques liées à la programmation de fonctions humaines comme la vision, la reconnaissance des formes ou l’intelligence artificielle.
Complexité Durée pour $N = 10^6$
Logarithmique : $O(log N)$ 10 ns
Linéaire : $O(N)$ 1 ms
Quadratique : $O(N^2)$ 1/4 heure
Polynomiale : $O(N ^k)$ 30 ans si $k=3$
Exponentielle : $O(2^N)$ plus de $10^{300000}$ milliards d’années

Ordres de grandeur des durées d’exécution d’un problème de taille $10^6$ sur un ordinateur à un milliard d’opérations par seconde (« Informatique pour tous en CPGE », éditions Eyrolles).

Quelques règles simples permettant de déterminer la complexité d’un algorithme

Nous allons introduire, dans cette partie, quelques règles simples qui permettent de se faire une idée de l’efficacité d’un algorithme :

  • Une affectation ou l’évaluation d’une expression ont un temps d’exécution petit. Cette durée constitue souvent l’unité de base dans laquelle on mesure le temps d’exécution d’un algorithme.
  • Le temps pris pour exécuter une séquence d’instrutions p q est la somme des temps pris pour exécuter les instructions p puis q.
  • Le temps pris pour exécuter un test Si (b) Alors p Sinon q FinSi est inférieur ou égal au maximum des temps pris pour exécuter les instructions p et q, plus une unité qui correspond au temps d’évaluation de l’expression b.
  • Le temps pris pour exécuter une boucle Pour i variant de 1 à m par pas de 1 Faire p FinPour est $m$ fois le temps pris pour exécuter l’instruction p si ce temps ne dépend pas de la valeur de i. En particulier, quand deux boucles sont imbriquées, le corps de la boucle interne est répété à cause de cette boucle, mais aussi parce qu’elle-même est répétée dans son intégralité. Ainsi, si les deux boucles sont répétées respectivement $m$ et $m\rq$ fois, alors le corps de la boucle interne est exécuté $m \times m\rq$ fois en tout.
    Quand le temps d’exécution du corps de la boucle dépend de la valeur de l’indice $i$, le temps total d’exécution de la boucle est la somme des temps d’exécution du corps de la boucle pour chaque valeur de $i$.
  • Le cas des boucles Tantque est plus complexe puisque le nombre d’itérations n’est en général pas connu à priori. Il doit être évalué au cas par cas.

Pour chacun des programmes suivants, dire en fonction de $n$ quel est le nombre d’opérations op que le programme effectue. Justifier votre résultat.

1
2

Pour i de 1 à n Faire 
    op

1
2

Pour i de 1 à n Faire 
    op; op

1
2
3

Pour i de 1 à n Faire
    Pour j de 1 à n Faire 
        op

1
2
3
4

Pour i de 1 à n Faire 
    Pour j de 1 à n Faire
        Pour k de 1 à n Faire
            op

1
2
3
4
5
6

Pour i de 1 à n Faire 
    op; op
     Pour j de 1 à n Faire
         op
         Pour k de 1 à n Faire 
            op

1
2
3

Pour i de 1 à n Faire
    Pour j de 1 à i Faire 
        op

1
2
3
4
5
6

i ⟵ 1
j ⟵ 1
TantQue (i ≤ m) et (j ≤ n) Faire
    op
    i ⟵ i + 1 
    j ⟵ j + 1

1
2
3
4
5
6

i ⟵ 1
j ⟵ 1
TantQue (i ≤ m) ou (j ≤ n) Faire
    op
    i ⟵ i + 1 
    j ⟵ j + 1

1
2
3

Tant que n > 0 Faire 
    op
    n ⟵ n // 2

Comment illustrer l’influence du nombre d’éléments passés en entrée

Quelques complexités à tout de suite identifier

En utilisant la fonction time du module time, écrire le code de fonctions qui :

  1. montre que le temps d’accès à un élément d’une liste est en $O(1)$ ;
  2. montre que la recherche linéaire dans une liste est en $O(N)$ ;
  3. met en évidence la complexité de l’opérateur Python in ;
  4. montre que la recherche linéaire dans une liste à deux dimensions est en $O(N^2)$ ;
  5. montre que la recherche dichotomique dans une liste triée est en $O(\log(N))$.

Terminaison d’un algorithme itératif : variant de boucle

La structure qui généralement doit retenir l’attention lors de l’analyse de la terminaison d’un algorithme est la structure de boucle.

On appelle variant d’une boucle une fonction qui a pour variables les variables du problème, qui retourne une valeur entière positive et qui décroît à chacune des itérations de la boucle, jusqu’à s’annuler ou prendre une valeur constante négative qui dépend de la condition d’arrêt de la boucle.

La découverte d’un variant de boucle permet de conclure que la boucle se termine puisqu’il n’existe aucune suite infinie strictement décroissante d’entiers naturels.

Exemple 1 : Calcul de la plus petite puissance de deux supérieure ou égale à un entier $n$

Algorithme 1

Fonction : plusPetitePuissance(n)
Entrée : entier naturel n
Sortie : entier naturel $p$ dont la valeur est égale à la plus petite puissance de deux supérieure ou égale à $n$.
Début
$p \longleftarrow 1$
TantQue $p < n$ Faire
$p \longleftarrow 2 p$
FinTantQue
Fin

La fonction $f$ d’expression $f(p) = n - p$ est-elle un variant de boucle ?

  • $f(p)$ est un entier positif.
  • Tant que $p < n$, $f(p) > 0$
  • $f$ décroît sur l’ensemble des valeurs de $p$ puisque $$f(p_{i+1}) - f(p) = n - p_{i+1} - n + p_{i} = p_{i} - p_{i+1} = p_{i} - 2p_{i} = - p_{i} <0$$
  • Condition d’arrêt : $p_{max} \geqslant n$, donc $f (p_{max}) \leqslant 0$.

La fonction $f$ est un variant de boucle et la boucle se termine donc bien.

Exemple 2 : Palindrome

Algorithme 2

Fonction : palindrome(m)
Entrée : chaîne de caractères m
Sortie : booléen Vrai si la chaîne de caractères m est un palindrome, Faux sinon
Début
$i \longleftarrow 0$
$j \longleftarrow \text{longueur} (m) - 1$
TantQue $i \leqslant j$ Faire
Si $m[i] = m[j]$ Alors
$i \longleftarrow i + 1$
$j \longleftarrow j - 1$
Sinon
Renvoyer Faux
FinSi
FintantQue
Renvoyer Vrai
Fin

  1. Décrire au moyen d’un tableau indiquant l’évolution des valeurs des variables le fonctionnement de l’algorithme 2 pour la chaîne de caractères « sauras » puis pour la chaîne de caractères « radar ».
    Remarque : Le premier élément d’une chaîne a pour indice 0.
Réponse

  • Pour l’entrée « sauras » :
    $i$ : 0, 1, 2
    $j$ : 5, 4, 3
    La fonction retourne Faux.

  • Pour l’entrée « radar » :
    $i$ : 0, 1, 2, 3
    $j$ : 4, 3, 2, 1
    La fonction retourne Vrai.

  1. Montrer que $f(i, j) = j - i$ est un variant de la boucle TantQue.
Réponse

$f(i, j) = j - i$ est-elle un variant de boucle ?

  • Tant que $j > i$, $f(i, j)$ est un entier positif et $f(i, j) = j - i > 0$.
  • $f (i+1, j-1) = j - 1 - (i + 1) = j - 1 - i - 1 = j - i - 2 = f(i, j) - 2 < f(i, j)$.
    La fonction est donc décroissante sur l’ensemble des valeurs de $i$ et de $j$.
  • Condition d’arrêt : $i > j$, donc $f(i, j) = j - i < 0$
  1. En déduire que la boucle TantQue se termine.
Réponse

La fonction $f$ est un variant de boucle. La boucle se termine donc bien.

Correction d’un algorithme itératif : invariant de boucle

On appelle invariant d’une boucle une propriété qui, si elle est vraie avant l’exécution d’une itération, le demeure après l’exécution de l’itération. Un invariant de boucle doit être vrai avant de commencer la boucle et est alors garanti de rester correct après chaque itération de la boucle. En particulier, l’invariant sera toujours vrai à la fin de la boucle.

Les boucles et la récursivité étant fondamentalement similaire, il y a peu de différence entre démontrer un invariant de boucles et prouver qu’un programme est correct en utilisant un raisonnement par récurrence.

Exemple 3 : Calcul de $2^n$

Algorithme 3

Fonction : calculPuissanceDeux(n)
Entrée : entier naturel $n$
Sortie : entier naturel $p$ dont la valeur est égale à $2^n$
Début
$p \longleftarrow 1$
Pour $k$ allant de 1 à $n$ faire
$p \longleftarrow 2 p$
FinPour
Fin

La propriété « À chaque tour de boucle $p$ est une puissance de 2 » est un invariant de boucle. En effet :

  • Initialisation : Avant d’entrer dans la boucle : $p = 1 = 2^0$.

  • Conservation : On suppose l’invariant vérifié au tour $i$ de la boucle : $p = 2^i$. Au tour $i + 1$, $p_{i + 1} = p_{i} \times 2 = 2^i \times 2 = 2^{i + 1}$.

  • Terminaison : La boucle réalise $n$ tours ; au dernier tour $p = 2^{n - 1} \times 2 = 2^n$

La proposition est donc bien un invariant de boucle et on peut conclure que l’algorithme est correct.

Exemple 4 : Quotient et reste de la division euclidienne d’un entier positif par un entier strictement

Algorithme 4

Fonction : division(a, b)
Entrée : entiers naturels $a$ et $b$
Sortie : Quotient $q$ et reste $r$ de la division euclidienne de l’entier naturel $a$ par l’entier naturel $b$
Début
$q \longleftarrow 0$
$r \longleftarrow a$
TantQue $r \geqslant b$ Faire
$q \longleftarrow q + 1$
$r \longleftarrow r - b$
FinTantQue
Renvoyer $q, r$
Fin

  1. Décrire le fonctionnement de l’algorithme pour l’entrée (a = 17, b = 5) au moyen d’un tableau indiquant l’évolution des valeurs des variables au fil des itérations.
Réponse

$$ \begin{array}{c : c : c : c : c} a & 17 & 17 & 17 & 17\cr \hdashline b & 5 & 5 & 5 & 5 \cr \hdashline q & 0 & 1 & 2 & 3 \cr \hdashline r & 17 & 12 & 7 & 2 \cr \end{array} $$

  1. Montrer que la boucle TantQue se termine en utilisant un variant de boucle.
Réponse

La fonction $f(r) = r - b$ peut-elle être un variant de boucle ?

  • $f(r) = r -b$ est un entier.
  • Pour n’importe quel tour de boucle $r \geqslant b$, donc $f(r) = r -b \geqslant 0$.
  • Soit $r_2 = r_1 - b$.
    $f(r_2) = r_2 - b = r_1 - b - b = f(r_1) - b \leqslant f(r_1)$.
    La fonction $f$ est décroissante.
  • Condition d’arrêt : $r < b$, donc $f(r, b) = r - b < 0$.

La fonction $f$ est bien un variant de boucle et cette boucle se termine.

  1. Montrer que la propriété $a =bq+ r$ est un invariant de la boucle TantQue, en déduire que l’algorithme produit le résultat attendu.
Réponse

Si la propriété $a =b q+ r$ est un invariant de boucle, elle doit être vraie avant d’entrer dans la boucle, à chaque tour de boucle et une fois la boucle terminée.

  • Initialisation : Avant d’entrer dans la boucle, $q=0$ et $r=a$. Donc on a bien $a = 0 \times b + a$.
  • Conservation : On suppose la propriété vraie au rang $k$ quelconque de la boucle : $a = b q_k + r_k$.
    Au rang $k+1$, $q_{k+1} = q_{k} + 1$ et $r_{k+1} = r_k - b$. Donc $a = b q_{k+1} + r_{k+1} = b q_{k} + b + r_k - b = b q_k + r_k$.
  • Terminaison : La boucle s’arrête lorsque $r < b$. Au dernier tour de la boucle on a donc bien $a=b q + r$.

La propriété $a =bq+ r$ est bien un invariant de boucle et le programme est correct.

  1. Écrire le code Python implémentant l’algorithme 4. La spécification de la fonction est la suivante :
1
2
3
4
5

def division_euclidienne(a: int, b: int) -> tuple[int, int]:
    """
    Calcule la division euclidienne de l'entier naturel a par l'entier naturel b.
    Retourne les entiers naturels q et r, quotient et reste de cette division.
    """
Réponse 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def division_euclidienne(a: int, b: int) -> tuple[int, int]:
    """
    Calcule la division euclidienne de l'entier naturel a par l'entier naturel b.
    Retourne les entiers naturels q et r, quotient et reste de cette division.
    """
    q = 0
    r = a
    while r >= b:
        q = q + 1
        r = r - b
    return q, r
  1. Écrire un jeu de tests pour la fonction division_euclidienne.
Réponse 
1
2
3

assert division_euclidienne(1, 2) == (0, 1)
assert division_euclidienne(2, 1) == (2, 0)
assert division_euclidienne(17, 5) == (3, 2)

Exercices

Exercice

On considère la fonction suivante :

1
2
3
4
5
6
7

def power(n: int) -> int:
    p = 1
    i = 0
    while i < n:
        p = p * 2
        i = i + 1
    return p

  1. Quel calcul ce code réalise-t-il ?

  2. Écrire un jeu de test pour cette fonction.

  3. Démontrer que l’algorithme se termine.

  4. Démontrer que l’algorithme est correct.

  5. Déterminer la complexité de cet algorithme.

Réponses

  1. power calcule $2^n$.

1
2
3

assert power(0) == 0
assert power(1) == 2
assert power(10) == 1024

  1. $f(i) = n - i$ est-il un variant de boucle ?

    • $f(0) = n$ est un entier naturel.
    • $f(i+1) - f(i) = n - i - 1 - n + i = -1$
      La suite est strictement décroissante.
    • $i_{max} = n$ donc $f(i_{max}) = n - i_{max} = n - n = 0$.
      $f(i)$ est un variant de boucle, l’algorithme se termine.

  2. Invariant de boucle : “À l’issue de chaque itération, $p=2^i$.”

    • Initialisation : À l’entrée de la boucle, $i=0$, $2^i = 2^0 = 1 = p$.
    • Conservation : On suppose qu’à l’issue du tour de boucle de compteur $k$, $p_k = 2^k$.
      $p_{k+1} = p_k \times 2 = 2^k \times 2 = 2^{k+1}$.
    • Terminaison : Lors du dernier tour de boucle, $i = n - 1$, le calcul effectué est donc $p = 2^{n-1} \times 2= 2^n$.
      L’algorithme est correct.

Exercice

On considère la suivante :

1
2
3
4
5
6
7

def maxer(s: list[float]) -> float:
    while len(s) > 1:
        if s[0] > s[1]:
            s.pop(1)
        else:
            s.pop(0)
    return s.pop(0)

  1. Quelle opération ce code réalise-t-il ?

  2. Écrire un jeu de test pour cette fonction.

  3. Démontrer que l’algorithme se termine.

  4. Démontrer que l’algorithme est correct.

  5. Déterminer la complexité de cet algorithme.

  6. Existe-t-il un ou des algorithmes qui réalisent la même opération plus efficacement ?

Réponses

  1. la fonction trouve le plus grand élément dans la liste passée en argument.

  3. $f(i) = i - 1$ avec $i=\text{len}(s)$ est-il un variant de boucle ?

    • $f(i_0) = len(s) - 1$ est un entier naturel si la liste s n’est pas vide.
    • $f(i_{k+1}) - f(i_k) = len(s[1:]) - 1 - len(s) + 1 = len(s[1:]) - len(s) < 0$
      La fonction $f$ est strictement décroissante.
    • $i_{der} = 1$, $f(i_{der}) = 1 - 1 = 0$.
      $f$ est un variant de boucle et la boucle se termine.

  4. Invariant de boucle :

Exercice

On considère la fonction somme_premiers_entiers qui implémente l’algorithme :

Algorithme 5

Fonction : somme_premiers_entiers(n)
Entrée : entier naturel $n$
Sortie : somme des n premiers entiers naturels
Début
$\text{somme} \longleftarrow 0$
$i \longleftarrow 1$
TantQue $i \leqslant n$ Faire
$\text{somme} \longleftarrow somme + 1$
$i \longleftarrow i + 1$
FinTantQue
Renvoyer somme
Fin

  1. Implémenter en Python l’algorithme proposé. Ne pas oublier la spécification de la fonction.

  2. Écrire un jeu de test pour cette fonction.

  3. Prouver que la boucle se termine à l’aide du variant de boucle $f(n, i) = n - i$ où $i$ est le compteur de la boucle.

  4. Prouver que la proposition : « au début du tour du kième tour de la boucle, la variable somme est égale à la somme des $k-1$ premiers entiers naturels » est un invariant de boucle. En déduire que l’algorithme est correct.

  5. Quelle est la complexité de cet algorithme ?

Réponses 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def somme_premiers_entiers(n: int) -> int:
    """
    Calcule la somme des n premiers entiers.
    
    HYPOTHÈSE : n entier naturel
    """
    somme = 0
    i = 0
    while i <= n:
        somme = somme + i
        i = i + 1
    return somme

1
2
3

assert somme_premiers_entiers(0) == 0
assert somme_premiers_entiers(1) == 1
assert somme_premiers_entiers(12) == 12 * (12 + 1) / 2
  • Pour n’importe quel tour de boucle, on a $i \leqslant n$. Donc $f(n, i) = n - i \geqslant 0$ ;
  • Au rang $k+1$, $i_{k+1} = i_k + 1$ donc $f(n, i_{k+1}) = n - i_{k+1} = n - i_k - 1 = f(n, i_k) - 1 < f(n, i_k)$. La fonction $f$ décroit lorsque la boucle progresse.
  • condition d’arrêt : $i>n$, donc $f(n,i) = n - i < 0$.

La fonction $f$ est positive, décroissante lorsque la boucle « tourne » et finalement prend une valeur négative lorsque la boucle est terminée ; c’est un variant de boucle.
La présence d’un variant de boucle nous assure que la boucle se termine.

  • Initialisation : Avant d’entrer dans la boucle, $\text{somme} = 0$.
  • Conservation : On suppose que $\text{somme} = 0 + 1 + \ldots + k -1$ au début de la kième boucle. Pendant la kième boucle, on a $\text{somme} = \text{somme} + k = 0 + 1 + \ldots + k -1 + k$.
    Au début de la $k+1$ième boucle, on a donc bien $\text{somme} = 0 + 1 + \ldots + k$.
  • Terminaison : La boucle s’arrête dès que $i > n$. Donc au début du $n+1$ième tour (tour de boucle qui n’aura jamais lieu), on a bien $\text{somme} = 0 + 1 + \ldots + n$.

La proposition est bien un invariant de boucle, elle nous assure que le programme est corret.

Algorithmique  Complexité  Terminaison  Invariant  Variant  Correction 

Suggestions de lecture :