Listes Chaînées, présentation

... et implémentation à l'aide d'une classe

Tableaux

  • Un tableau est une structure de données dans laquelle les éléments, tous de même type, occupent des positions contiguës en mémoire.
  • Le nombre d’éléments qu’un tableau peut contenir est déterminé à la création d’un tableau.
Type Python Type Opération Exemple Complexité
N’existe pas Tableau Accès à un élément tab[i] $O(1)$
Modification d’un élément tab[i] = x $O(1)$
Effacement d’un élément retire(tab, i) $O(n)$
Insertion d’un élément insere(tab, x, i) $O(n)$
Recherche d’un élément est_dans(tab, x) $O(n)$
  • La structure de données appelée « liste » dans le langage Python est implémentée à l’aide de tableaux dynamiques.

Remarque : Dans la suite de ce document, on va considérer que la liste Python tab, créé par l’instruction tab = [i for i in range(20)] est de longueur fixe. Elle se comporte alors comme un tableau.

Pourquoi la recherche d’un élément dans un tableau quelconque (non trié donc) est en $O(N)$ ?

  1. Écrire le prédicat est_dans de spécification :
1
2
3
4
5
6

def est_dans(tab: List[int], n: int) -> bool:
    """
    Recherche si la valeur n est présente au moins une fois
    dans le tableau tab.
    Algorithme itératif.
    """

  1. Écrire un jeu de tests.

  2. (Facultatif) Écrire le prédicat est_dans_rec de spécification :

1
2
3
4
5
6

def est_dans_rec(tab: List[int], n: int, i: int = 0) -> bool:
    """
    Recherche si la valeur n est présente au moins une fois
    dans le tableau tab.
    Algorithme récursif, i est l'indice de recherche.
    """
  1. Quelle est la complexité des algorithmes précédents en fonction de $N$, la taille du tableau ?
Réponse
  • Dans l’algorithme itératif, dans le pire des cas (valeur absente du tableau) $N$ tours de boucle sont effectués.
  • Dans l’algorithme récursif, $N$ appels récursifs sont effectués.

L’algorithme est donc en $O(N)$.

Pourquoi l’insertion d’un élément dans un tableau est en $O(N)$ ?

Dans cette partie, on imagine que le tableau a cette allure :

1 1 2 3 4 5 vide vide vide

Si on introduit, en position 1, la valeur 7. Le tableau est alors :

7 1 1 2 3 4 5 vide vide
Cette opération n’est possible, sans crainte de perdre des données, que si toutes les cellules du tableau ne contiennent pas des données. Toute fonction permettant l’insertion de valeurs doit donc avertir un utilisateur dans le cas contraire.

Remarque : Dans le code ci-dessous, les cellules seront considérées vides si elles contiennent la valeur None.

  1. Écrire la fonction insere dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def insere(tab: List[int], n: int, i: int) -> None:
    """
    Insère la valeur n à l'indice i du tableau tab.
    Algorithm itératif et en place.

    Lève une exception si le tableau est déjà plein.

    HYPOTHÈSE : la gestion des "trous" n'est pas assurée,
    l'algorithme se contente de décaler les valeurs vers 
    la droite.
    """
  1. (Facultatif) Écrire la fonction insere_rec dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def insere_rec(tab: List[int], n: int, i: int, k: int) -> None:
    """
    Insère la valeur n à l'indice i du tableau tab.
    Algorithm récursif et en place. k est l'indice de recherche. Sa première valeur doit être len(tab) - 1.

    Lève une exception si le tableau est déjà plein.

    HYPOTHÈSE : la gestion des "trous" n'est pas assurée,
    l'algorithme se contente de décaler les valeurs vers 
    la droite.
    """
  1. Quelle est la complexité des algorithmes précédents en fonction de $N$, la taille du tableau ?
Réponse
  • Dans le pire des cas (insertion à la première place du tableau), on déplace $N-1$ valeurs.

L’algorithme est donc en $O(N)$.

Structure de liste chaînée

Les listes chaînées constituent une structure de données :

  • de longueur modifiable ;
  • plus efficace que les tableaux lorsqu’il s’agit d’ajouter ou de retirer un élément (il n’est pas nécessaire de faire de la place en déplaçant les éléments) ;
  • qui servira de brique à l’élaboration d’autres structures de données.

Une liste chaînée permet de représenter une liste ; chaque élément de cette liste est une cellule contenant :

  • la valeur de l’élément à stocker ;
  • l’adresse mémoire de la cellule représentant l’élément suivant.

Remarque : le symbole $\perp$ marque la fin de la liste dans les schémas.

Comment implémenter une cellule ?

En langage Python, on peut implémenter une cellule à l’aide d’une classe, de listes ou de tuples.

  1. Définir la classe Cellule dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Cellule():
    """
    Implémentation d'une cellule de liste chaînée
    de nombres entiers.

    Attributs
    ---------
    valeur : int
        Valeur à stocker dans la liste
    suivante : Cellule
        Addresse de la cellule suivante (chaînée)
    """
La dernière cellule d’une liste chaînée devra pointer vers l’objet None qui représente donc une cellule vide.

  1. Instancier 3 objets c1, c2, c3, de type Cellule, dont les valeurs sont 1, 2, 3. Tous ces objets sont pour l’instant isolés (ils ne pointent vers aucune autre cellule si ce n’est la cellule vide None).

  2. Créer la liste lst à l’aide de ces trois objets.

  3. Comment aurait-on pu créer la liste lst en une seule instruction ?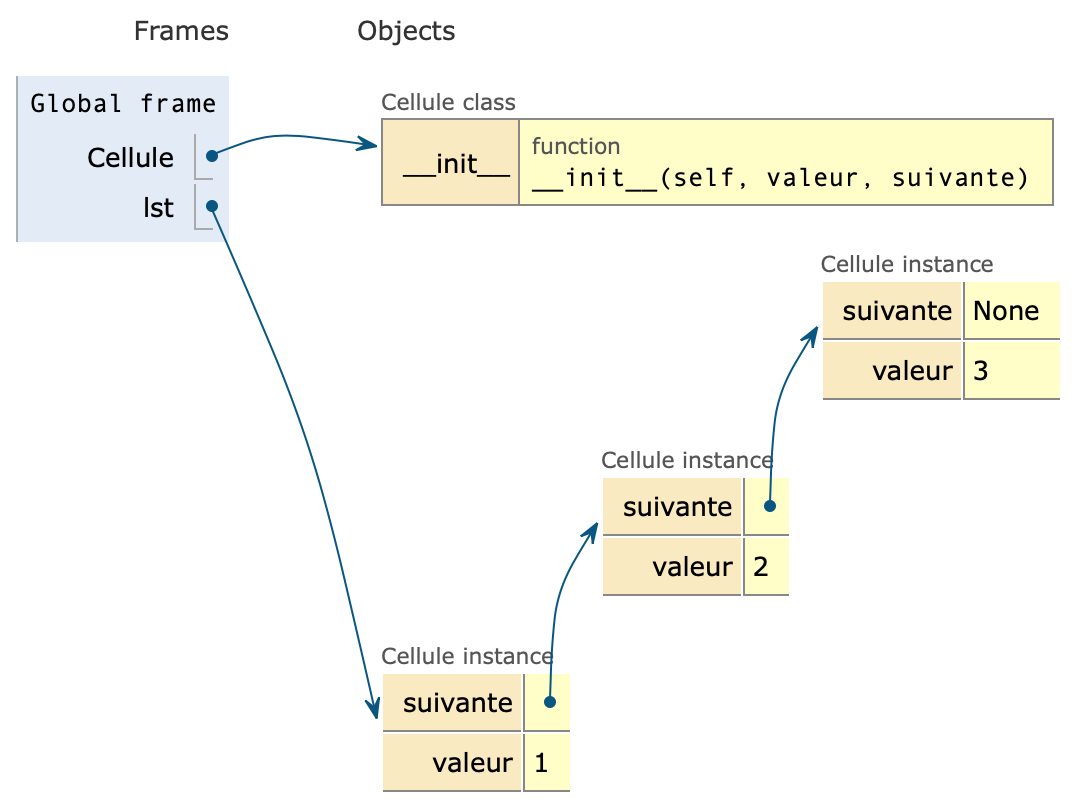

Les listes chaînées sont des structures fondamentalement récursives

Une liste chaînée est :

  • soit la liste vide (objet None) ;
  • soit constituée de son premier élément (objet de type Cellule) et du reste des éléments qui forment aussi une liste. Une liste chaînée est donc une structure récursive.

Une liste chaînée est-elle forcément homogène

Tout au long de ce document nous allons uniquement envisager des listes chaînées de nombres entiers. Rien n’impose, cependant, à l’attribut valeur de la classe Cellule d’être un entier. Chaque cellule peut même posséder des attributs valeur de type différent. Les listes chaînées peuvent donc être hétérogènes.

Quelques opérations sur les listes chaînées

Le point de vue envisagé dans la suite de ce document est celui de la programmation impérative : nous allons définir des fonctions qui vont modifier la liste chaînée.
Nous créerons une classe enveloppe dans un prochain document, de façon à ce notre liste chaînée ait la même interface qu’une liste Python.

Longueur d’une liste chaînée

  1. Écrire la fonction longueur dont la spécification est :
1
2
3
4
5
6

def longueur(lst: Cellule) -> int:
    """
    Détermine la longueur de la liste lst.

    Algorithme récursif.
    """
  1. Écrire la fonction longueur_iter dont la spécification est :
1
2
3
4
5
6

def longueur_iter(lst: Cellule) -> int:
    """
    Détermine la longueur de la liste lst.

    Algorithme itératif.
    """
  1. Déterminer la complexité du calcul de la longueur d’une liste.
Réponse

On réalise autant d’appels récursifs (ou de tours de boucles qu’il y a d’éléments dans la liste).
La complexité est donc en $O(N)$.

Affichage de tous les éléments d’une liste

  1. Écrire la fonction affichage_elements_liste dont la spécification est :
1
2
3
4
5

def affichage_elements_liste(lst: Cellule) -> None:
    """
    Affiche tous les éléments de la liste lst.
    Chaque élément est séparé par une tabulation "\t"
    """
  1. Définir la fonction list_to_str dont la spécification est :
1
2
3
4
5
6
7
8

def list_to_str(lst: Cellule, premier: bool = True) -> str:
    """
    Retourne une chaîne de caractères constituée de toutes
    les valeurs, sous la forme : "[valeur1, valeur2, ...]".

    premier est positionné à True si la valeur est la première
    de la liste et à False pour toutes les autres valeurs.
    """

Valeur du n-ième élément d’une liste

  1. Écrire la fonction n_ieme_element dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def n_ieme_element(lst: Cellule, i: int) -> int:
    """
    Retourne le n-ième élément de la liste. La convention
    suivie est celle de Python, le premier élément ayant
    l'indice i = 0.

    Algorithme récursif.

    Lève une exception si l'indice de la liste est trop grand.
    """
  1. Écrire la fonction n_ieme_element_iter dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def n_ieme_element_iter(lst: Cellule, i: int) -> int:
    """
    Retourne le n-ième élément de la liste. La convention
    suivie est celle de Python, le premier élément ayant
    l'indice i = 0.

    Algorithme itératif.

    Lève une exception si l'indice de la liste est trop grand.
    """
  1. Déterminer la complexité de la recherche du n-ième élément d’une liste.
Réponse
  • Si l’élément dont on cherche la valeur est le dernier de la liste il est nécessaire de faire $N$ appels récursifs (ou tours de boucles).
  • Si l’indice est hors des limites, il est ici aussi nécessaire de parcourir toute la liste avant de s’en rendre compte. L’algorithm est donc en $O(N)$.

Modification de la valeur d’une cellule sans modifier la structure de la liste

  1. Écrire la fonction modifier_n_ieme_element dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def modifier_n_ieme_element(lst: Cellule, i: int, valeur: int) -> None:
    """
    Modifie le n-ième élément de la liste. La convention
    suivie est celle de Python, le premier élément ayant
    l'indice i = 0.

    Algorithme récursif.

    Lève une exception si l'indice de la liste est trop grand.
    """

Ajout d’une valeur à la fin de la liste

  1. Écrire la fonction ajout_fin_liste dont la spécification est :
1
2
3
4
5
6
7

def ajout_fin_liste(lst: Cellule, valeur: int) -> None:
    """
    Ajout de valeur à la fin de la liste.
    La liste lst est modifiée.

    Algorithme récursif.
    """
  1. Quelle est la complexité de la fonction ajout_fin_liste ?
Réponse

On doit parcourir toute la liste pour ajouter un élément à la fin. La complexité est donc linéaire.

Ajout d’une valeur au début de la liste

  1. Écrire la fonction ajout_debut_liste dont la spécification est :
1
2
3
4
5
6
7

def ajout_debut_liste(lst: Cellule, valeur: int) -> Cellule:
    """
    Ajout de valeur au début de la liste.

    La nouvelle adresse de la tête de liste doit être
    retournée.
    """
  1. Quelle est la complexité de cette fonction ?
Réponse

$O(1)$

Retrait du dernier élément d’une liste

  1. Écrire la fonction retrait_dernier_element dont la spécification est :
1
2
3
4
5
6

def retrait_dernier_element(lst: Cellule) -> int:
    """
    Retire le dernier élément de la liste et le retourne.

    Algorithme récursif.
    """
  1. Quelle est la complexité de cette fonction ?
Réponse

Il faut parcourir la liste, donc $O(N)$.

Retrait du premier élément d’une liste

  1. Écrire la fonction retrait_premier_element dont la spécification est :
1
2
3
4
5
6
7

def retrait_premier_element(lst: Cellule) -> tuple[int, Cellule]:
    """
    Retire le premier élément de la liste et le retourne.

    La nouvelle adresse de la tête de liste doit être 
    retournée.
    """
  1. Quelle est la complexité de cette fonction ?
Réponse

$O(1)$.

Retrait du n-ième élément d’une liste

  1. Écrire la fonction retrait_n_ieme_element dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def retrait_n_ieme_element(lst: Maillon, i: int) -> int:
    """
    Retire le n-ième élément de la liste lst. La convention
    suivie est celle de Python, le premier élément ayant
    l'indice i = 0.
    
    Algorithme récursif.
    
    Lève une exception si l'indice de la liste est trop grand,
    ne prend pas en charge le retrait du premier élément.
    """
  1. Quelle est la complexité de cette fonction ?
Réponse

Le retrait en lui-même est en $O(1)$ mais il faut arriver jusqu’à la valeur. L’ensemble est donc en $O(N)$.

Concaténation de deux listes

On appelle concaténation de deux listes l’opération consistant à mettre bout à bout les deux listes.
  1. Écrire la fonction concatener dont la spécification est :
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def concatener(lst1: Cellule, lst2: Cellule) -> Cellule:
    """
    Concatène les listes lst1 et lst2. Une nouvelle liste est
    créée et retournée.
    Les éléments de la première liste sont copiés alors que ceux 
    de la deuxième sont insérés. lst1 et lst2 ne sont donc pas modifiées.

    ATTENTION : tout élément de lst partagé avec lst2 modifié l'est aussi 
    dans lst2.
    
    Algorithme récursif.
    """
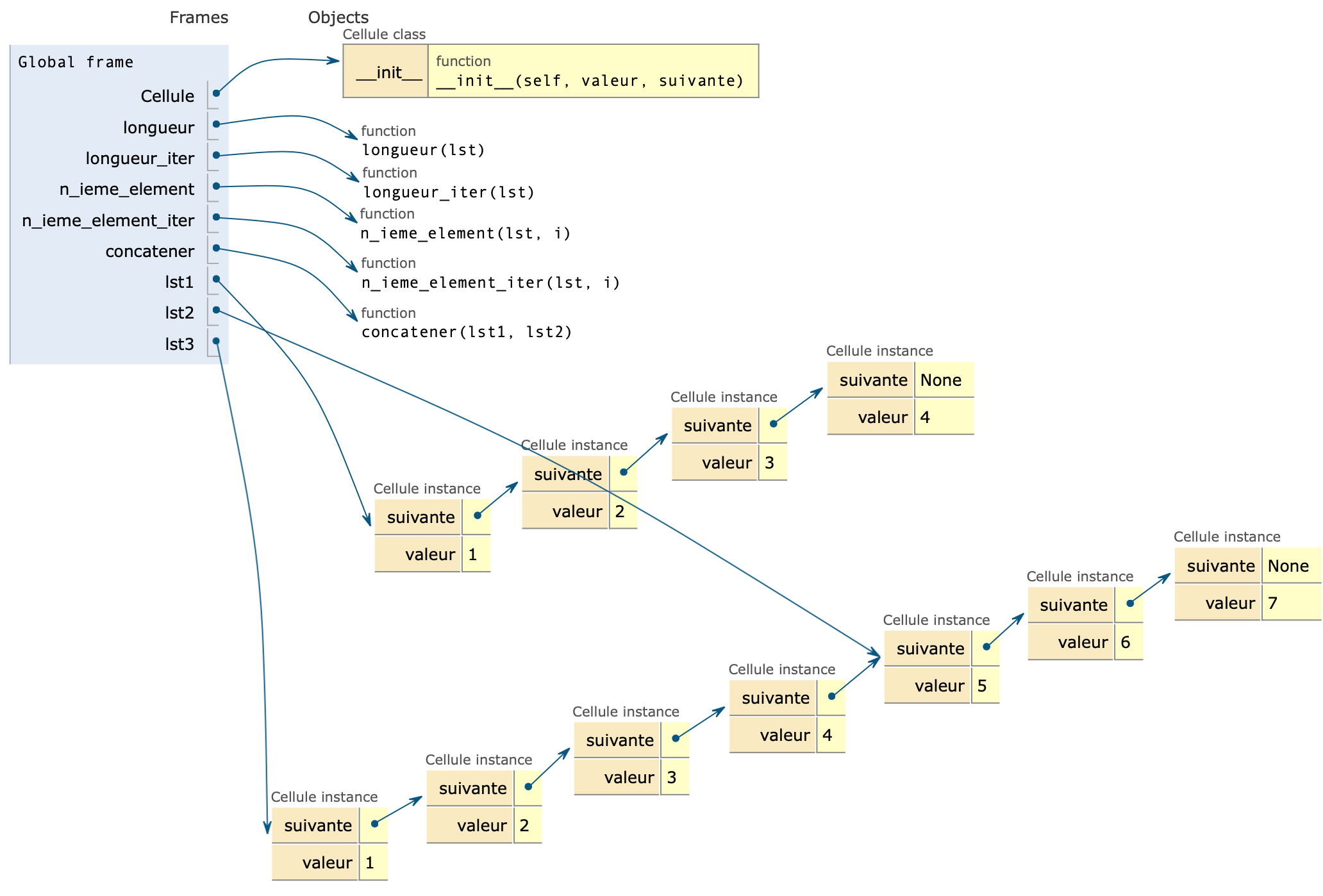
  1. Écrire la fonction copie dont la spécification est :
1
2
3
4
5
6

def copie(lst: Cellule) -> Cellule:
    """
    Réalise une nouvelle copie de la liste lst.

    Algorithme récursif.
    """
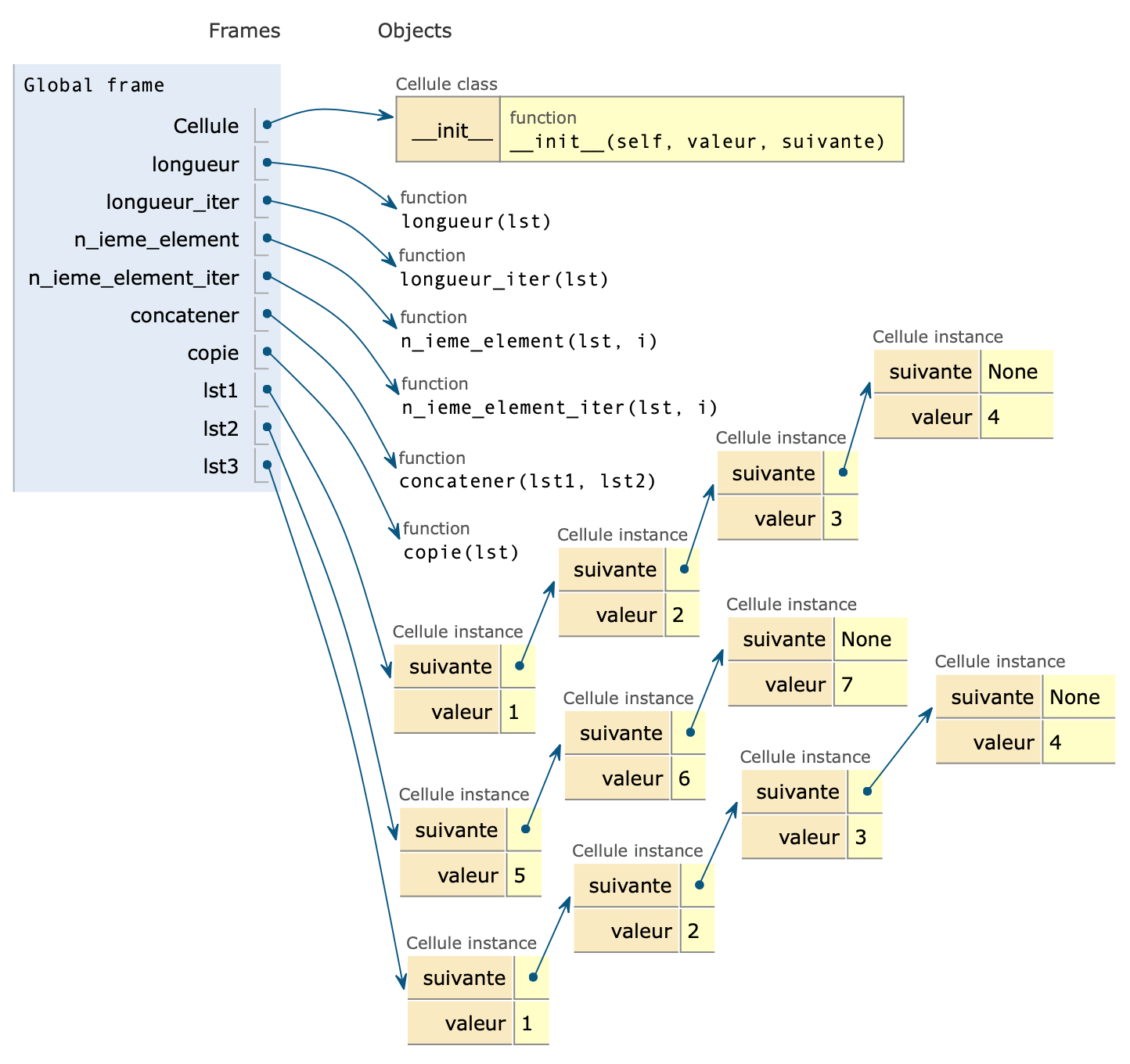
  1. Se servir de la fonction copie pour écrire la fonction concatener_avec_copie_integrale dont la spécification est :
1
2
3
4
5
6
7

def concatener_avec_copie_integrale(lst1: Cellule, lst2: Cellule) -> Cellule:
    """
    Concatène les listes lst1 et lst2. Les éléments des listes lst1 et lst2
    sont recopiés pour former une nouvelle liste.
    
    Algorithme récursif.
    """
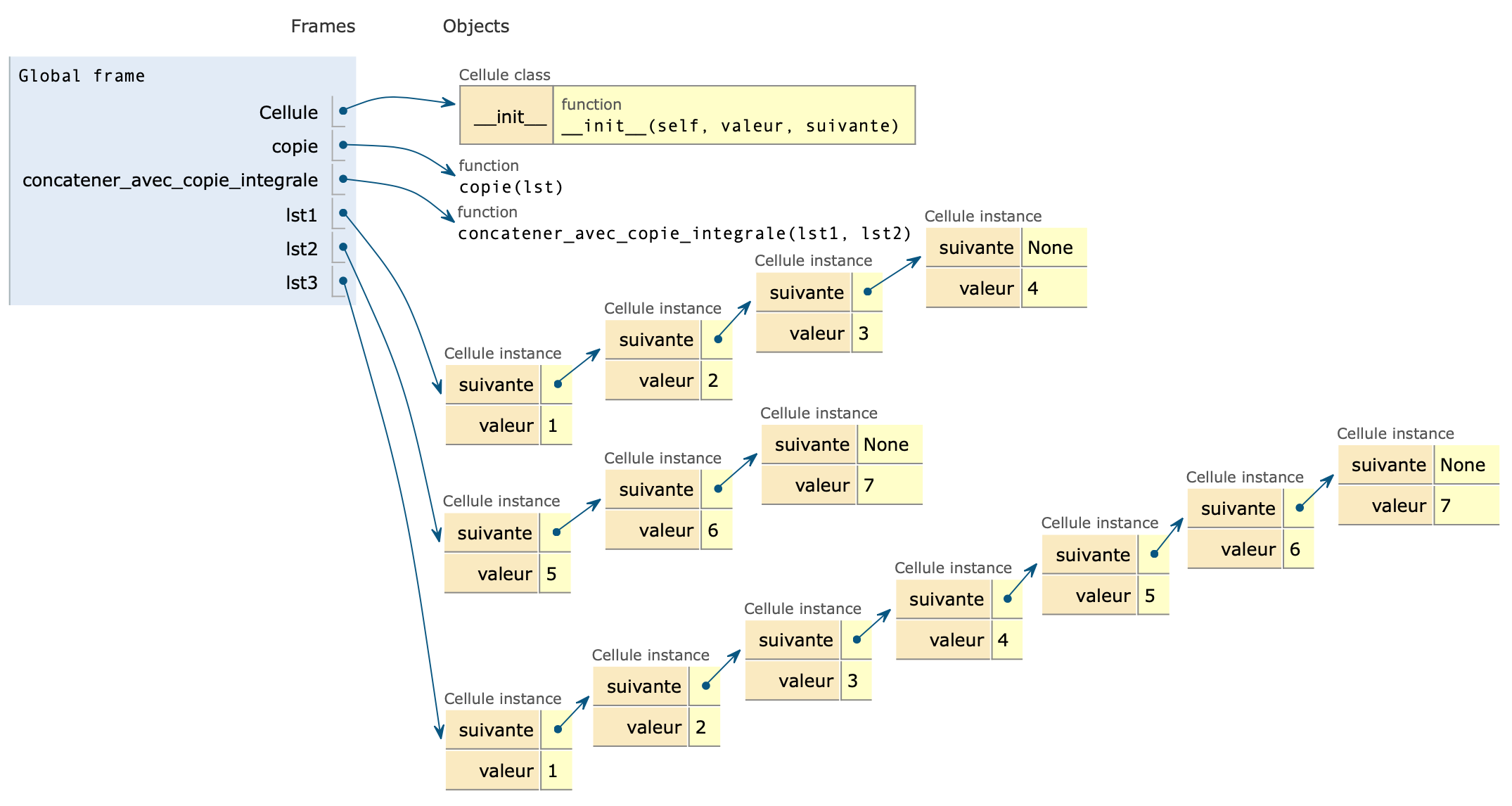
  1. Quelle est la complexité de la fonction concatener ? Même question pour la fonction concatener_avec_copie_integrale.
Réponse
  • Dans le premier cas, il est nécessaire de recopier tous les éléments de lst1. La complexité est donc linéaire et dépend du nombre d’élements de lst1.
  • Dans le second cas, on recopie tous les éléments de lst1 et de lst2. La complexité est donc linéaire et est la somme du nombre d’éléments de lst1 et de lst2.

Renverser une liste

  1. Écrire la fonction renverser dont la spécification est :
1
2
3
4
5
6
7

def renverser(lst: Cellule) -> Cellule:
    """
    Retourne une nouvelle liste formée des éléments de lst à l'envers. 
    Les éléments peuvent avoir été recopiés ou pas.

    Algorithme récursif.
    """

Remarque. Cette fonction doit s’appuyer sur les fonctions concatener ou concatener_avec_copie_integrale.

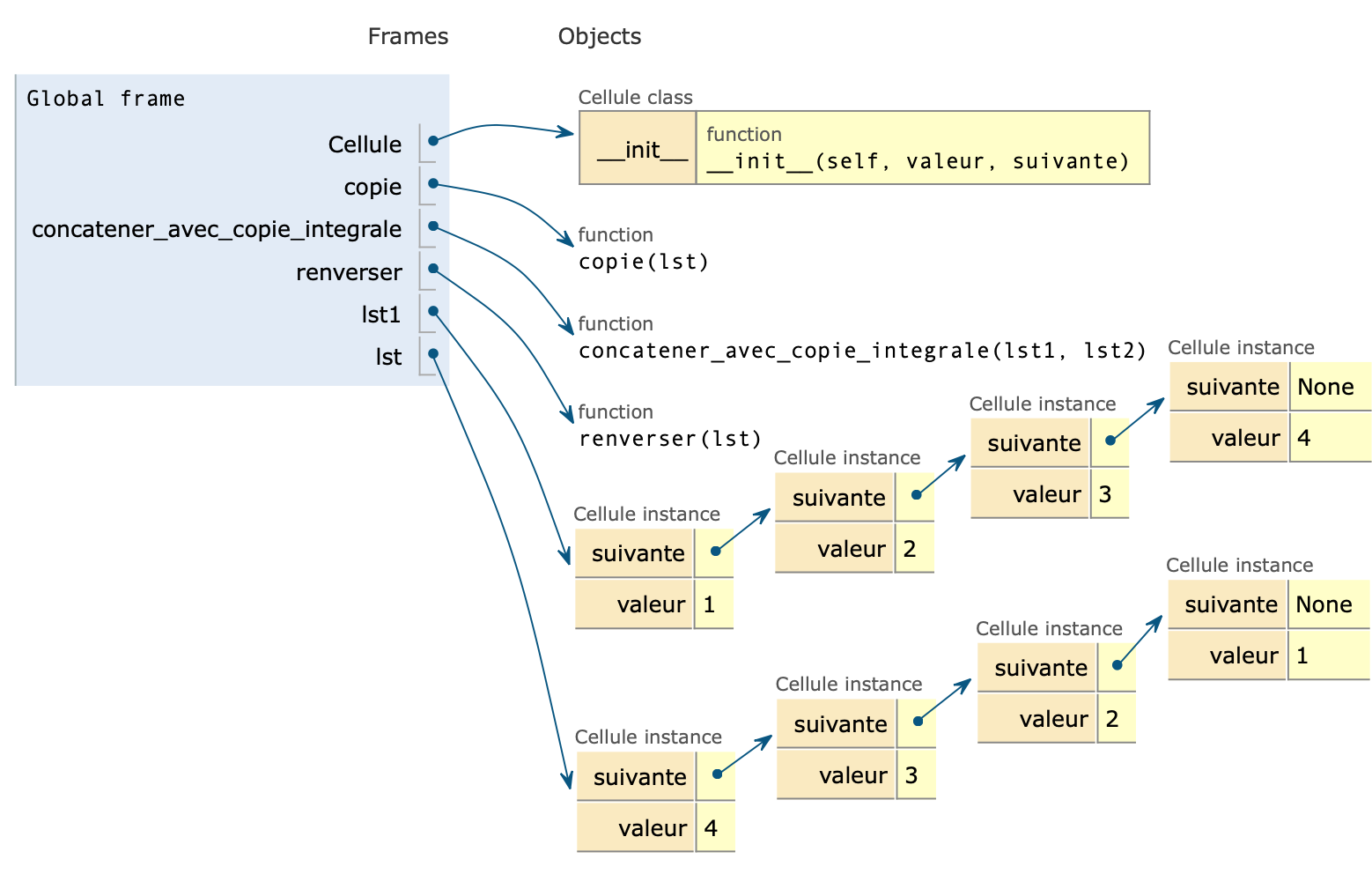
Remarque. Cet algorithme est particulièrement inefficace.

Conclusion

  • Une liste chaînée est une structure de données utile pour représenter une séquence finie d’éléments.
  • Chaque élément est contenu dans une cellule, qui fournit, en plus de la valeur, un moyen pour accéder à la cellule suivante.
  • Les éléments d’une liste chaînée ne sont pas situés dans des emplacements contigüs en mémoire.
  • Les opérations sur les listes chaînées se programment sous la forme de parcours qui suivent ces liaisons, en utilisant la récursivité ou des boucles.

Une liste chaînée est un type abstrait de données qui doit, au minimum, fournir les fonctions suivantes :

  • insère : insère un élément dans la liste ;
  • supprime : supprime et renvoie l’élément de position spécifié de la liste ;
  • longueur : renvoie le nombre d’éléments de la liste ;
  • est_vide : détermine si la liste est vide ou pas ;
  • nième_élément : retourne la valeur du nième élément depuis le début.
Action Liste chaînée Tableau Tableau dynamique
Accès à un élément $O(n)$ $O(1)$ $O(1)$
Insertion/suppression du 1er élément $O(1)$ $O(n)$ (si place) $O(n)$
Insertion à la fin $O(n)$ $O(1)$ (si place) $O(1)$ (si place)
$O(n)$ (si pas de place)
Suppression du dernier élément $O(n)$ $O(1)$ $O(1)$
Insertion/suppression au milieu $O(n)$ $O(n)$ (si place) $O(n)$

Quelques exemples d’utilisation des listes chaînées

  • Les logiciels de visualisation d’images utilisent parfois une liste chaînée pour afficher les images précédentes et suivantes à l’aide des boutons « précédent » et « suivant ».

  • Des navigateurs Web peuvent utiliser une liste chaînée pour accéder aux pages à l’aide des boutons « précédent » et « suivant ».

  • Les boutons « précédent » et « suivant » des lecteurs de musique peuvent utiliser une liste chaînée doublement/circulaire.

  • Les tracés et les formes sur le canevas, de MS-Paint sont connectés via une liste chaînée.

  • Le balayage « gauche/droite » sur Tinder utilise une liste doublement chaînée.

  • On peut garder la trace des tours dans un jeu multi-joueurs à l’aide d’une liste chaînée circulaire.

  • Les lignes de code dans un IDE peuvent être enregistrées dans une liste doublement chaînée.

Annexe : Tests possibles pour les fonctions codées

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

if __name__ == "__main__":
    #c1 = Cellule(1, None)
    #c2 = Cellule(2, None)
    #c3 = Cellule(3, None)
    #lst = c1
    #lst.suivante = c2
    #c2.suivante = c3

    lst = Cellule(1, Cellule(2, Cellule(3, Cellule(4, None))))
    affichage_elements_liste(lst)

    assert longueur(lst) == 4
    assert longueur_iter(lst) == 4

    assert n_ieme_element(lst, 0) == 1
    assert n_ieme_element(lst, 3) == 4
    #print(n_ieme_element(lst, 4))

    assert n_ieme_element_iter(lst, 0) == 1
    assert n_ieme_element_iter(lst, 3) == 4
    #print(n_ieme_element_iter(lst, 4))

    lst1 = Cellule(1, Cellule(2, Cellule(3, Cellule(4, None))))
    lst2 = Cellule(5, Cellule(6, Cellule(7, None)))
    lst3 = concatener_avec_copie_integrale(lst1, lst2)
    print(lst3)
    print(list_to_str(lst3))

    # Modification de la liste
    modifier_n_ieme_element(lst, 0, 12)
    assert n_ieme_element_iter(lst, 0) == 12

    # Ajout en fin de liste
    ajout_fin_liste(lst, Cellule(25, None))
    affichage_elements_liste(lst)
    print(list_to_str(lst))

    # Ajout en début de liste
    lst = ajout_debut_liste(lst, Cellule(34, None))
    affichage_elements_liste(lst)

    # Retrait dernier élément
    dernier = retrait_dernier_element(lst)
    print(dernier)
    affichage_elements_liste(lst)
Tableau  Tableau dynamique  Liste  Liste chaînée  Complexité 

Suggestions de lecture :