Dans ce document on introduit une méthode permettant d’évaluer numériquement une solution de l’équation $f (x) = 0$, avec $f$ une fonction de $\mathbb{R}$ dans $\mathbb{R}$ (lorsque la solution existe, bien sur) : la méthode de dichotomie.
- La méthode de dichotomie est efficace et converge relativement vite. De plus, les conditions de son utilisation sont assez simples : la fonction $f$ doit seulement être continue et changer de signe sur l’intervalle choisi ;
- La méthode de Newton converge étonnement vite ! Les conditions de son utilisation sont cependant plus contraignantes : la fonction $f$ doit être dérivable.
Méthode de la dichotomie
Le raisonnement à mettre en œuvre s’appuie sur le théorème des valeurs intermédiaires.
Théorème des valeurs intermédiaires
Soit $f: [a,b] \to \mathbb{R}$ une fonction continue sur un segment. Si $f(a) \cdot f(b) \leqslant 0$, alors il existe $\ell \in [a, b]$ tel que $f(\ell)=0$.
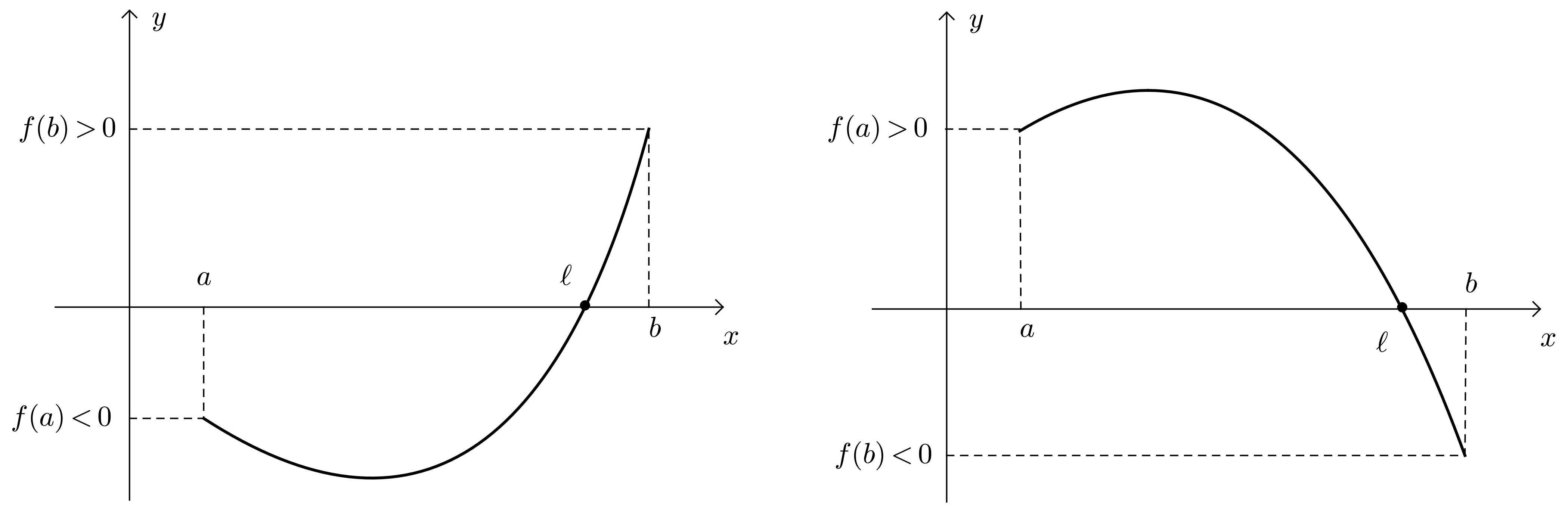
Principe de résolution du problème
-
On choisit un intervalle $[a, b]$ dans lequel on pense que la fonction $f$ s’annule une seule fois (il peut donc être nécessaire de limiter la largeur de cet intervalle).
-
Étape 1. On détermine les coordonnées du point milieu de l’intervalle : $\dfrac{a + b}{2}$
- Si $f(a) \cdot f \left( \dfrac{a + b}{2} \right) \leqslant 0$, le théorème des valeurs intermédiaires permet de conclure qu’il existe un point $c \in \left[a, \dfrac{a + b}{2} \right]$ tel que $f(c) = 0$.
- Si $f(a) \cdot f \left( \dfrac{a + b}{2} \right) \geqslant 0$, le théorème des valeurs intermédiaires permet de conclure qu’il existe un point $c \in \left[ \dfrac{a + b}{2}, b \right]$ tel que $f(c) = 0$. On est donc parvenu, à l’issu de cette étape, à définir un intervalle dans lequel $f(x) = 0$, de longueur moitié par rapport à l’intervalle initial.
-
Étape suivante. On répète le processus mis en œuvre dans l’Étape 1 pour l’intervalle $\left[a, \dfrac{a + b}{2} \right]$ ou $\left[ \dfrac{a + b}{2}, b \right]$.
-
Étapes suivantes. On continue à répéter le processus jusqu’à ce que l’intervalle soit de longueur inférieure à une longueur choisie (arbitrairement).
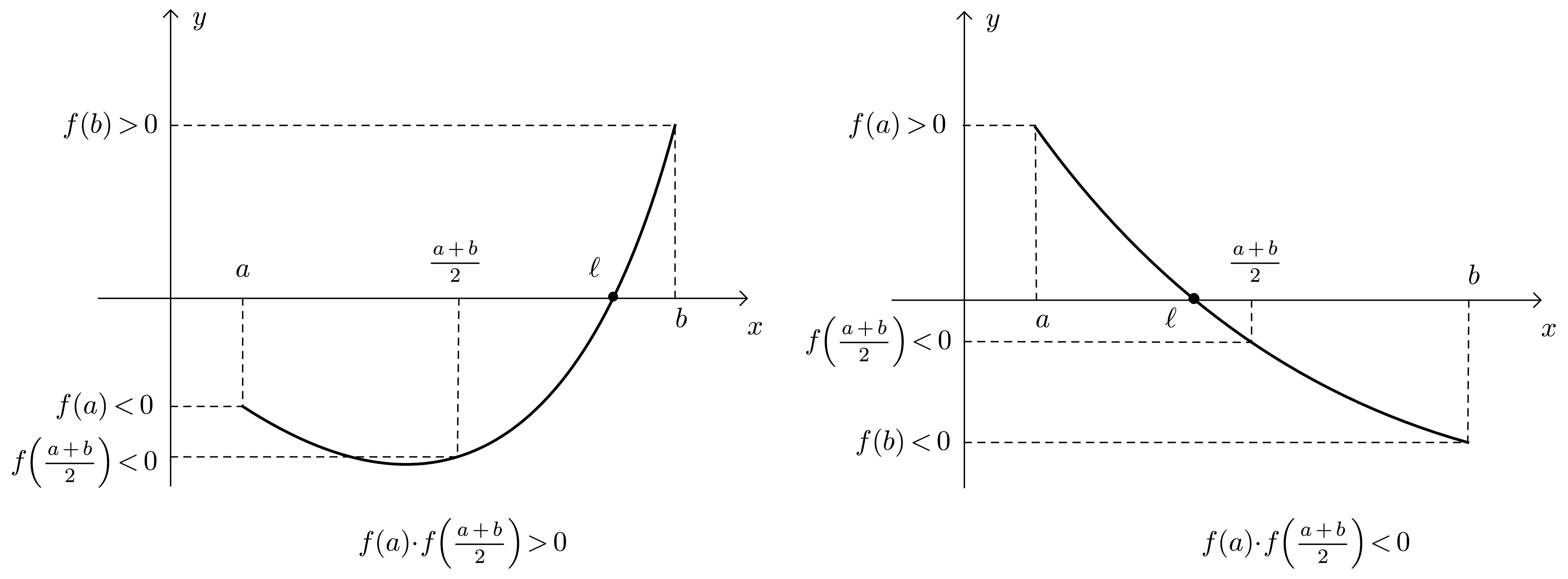
La méthode converge-t-elle réellement ?
-
On construit deux suites $(a_n)$ et $(b_n)$ qui évoluent comme les bornes de l’intervalle, et la suite $(x_n)$, zéro de $f$ pour chaque intervalle.
-
Au rang 0. On pose $a_0 = a$, $b_0 = b$. Comme $f (a) \cdot f (b) \leqslant 0$, il existe une solution, notée $x_0$, de l’équation $f (x) = 0$ dans l’intervalle $[a_0, b_0]$.
-
Au rang 1. Si $f (a_0) \cdot f \left( \dfrac{a_0 + b_0}{2} \right) \leqslant 0$, alors on pose $a_1 = a_0$ et $b_1 = \dfrac{a_0 + b_0}{2}$, sinon on pose $a_1 = \dfrac{a_0 + b_0}{2}$ et $b_1 = b_0$. Comme $f (a_1) \cdot f (b_1) \leqslant 0$, il existe une solution, notée $x_1$, de l’équation $f (x) = 0$ dans l’intervalle $[a_1, b_1]$.
-
Au rang $n$. On suppose construit un intervalle $[a_n, b_n]$, de longueur $\dfrac{b_n - a_n}{2^n}$, contenant une solution $x_n$ de l’équation $f (x) = 0$. Si $f (a_n) \cdot f \left( \dfrac{a_n + b_n}{2} \right) \leqslant 0$, alors on pose $a_{n + 1} = a_n$ et $b_{n + 1} = \dfrac{a_n + b_n}{2}$, sinon on pose $a_{n + 1} = \dfrac{a_n + b_n}{2}$ et $b_{n + 1} = b_n$. Comme $f (a_{n + 1}) \cdot f (b_{n + 1}) \leqslant 0$, il existe une solution, notée $x_{n + 1}$, de l’équation $f (x) = 0$ dans l’intervalle $[a_{n + 1}, b_{n + 1}]$.
-
-
Étude des suites construites Par construction : - $a_n \leqslant x_n \leqslant b_n$ - $(a_n)$ est une suite croissante, $(b_n)$ une suite décroissante. La limite de $(b_n - a_n)$ tend donc vers 0 lorsque $n$ tend vers $+ \infty$ : $$\lim (b_n - a_n) \xrightarrow [n \rightarrow + \infty]{} 0$$ Les suites $(a_n)$ et $(b_n)$ sont adjacentes. Elles admettent donc une même limite, $\ell$.
Par application du théorème des gendarmes, on peut aussi en conclure que $$\lim (x_n) \xrightarrow[n \rightarrow + \infty] \ \ell$$ et, comme $f$ est une fonction continue, $$f (\ell) = \lim_{n \rightarrow + \infty} f (x_n) = \lim_{n \rightarrow + \infty} 0 = 0$$ En conclusion, les suites $(a_n)$ et $(b_n)$ tendent vers la valeur $\ell$, solution de $f (x) = 0$.
Remarque
En pratique, on arrête le processus dès que $b_n - a_n = \dfrac{b - a}{2^n}$ est inférieur à la précision souhaitée.
Exemple : Approximation de $\sqrt{10}$
-
On définit la fonction $f$ définie par $f (x) = x^2 - 10$. $f$ est une fonction continue sur $\mathbb{R}$ qui s’annule en $\sqrt{10}$ et $-\sqrt{10}$.
-
On limite l’étude à l’intervalle $[3 ; 4]$ puisque : $f (3) = 3^2 - 10 = - 1 < 0$ et $f (4) = 4^2 - 10 = 6 > 0$ entraîne $\sqrt{10} \in [3 ; 4]$.
-
On écrit le processus itératif :
-
On pose $a_0 = 3$ et $b_0 = 4$. $f (a_0) \leqslant 0$ et $f (b_0) \geqslant 0$. $\dfrac{a_0 + b_0}{2} = \pu{3,5}$ donc $f \left( \dfrac{a_0 + b_0}{2} \right) = f (\pu{3,5}) = \pu{3,5}^2 - 10 = \pu{2,25} \geqslant 0$. $f (a_0) \cdot f \left( \dfrac{a_0 + b_0}{2} \right) \leqslant 0$, on en déduit que $\sqrt{10}$ est dans l’intervalle $[3 ; \pu{3,5}]$.
-
On pose $a_1 = 3$ et $b_1 = \text{3,5}$. $\dfrac{a_1 + b_1}{2} = \pu{3,25}$ donc $f \left( \dfrac{a_1 + b_1}{2} \right) = f (\pu{3,25}) = \pu{0,5625} \geqslant 0$. $f (a_1) \cdot f \left( \dfrac{a_1 + b_1}{2} \right) \leqslant 0$, on en déduit que $\sqrt{10}$ est dans l’intervalle $[3 ; \pu{3,25}]$.
-
On pose $a_2 = 3$ et $b_2 = \pu{3,25}$. $\dfrac{a_2 + b_2}{2} = \pu{3,125}$ donc $f \left( \dfrac{a_2 + b_2}{2} \right) = f (\pu{3,125}) = - \pu{0,23…} \leqslant 0$. $f (b_2) \geqslant 0$, $f$ s’annule sur l’intervalle $[\text{3,125} ; \pu{3,25}]$.
À ce stade, on a donc démontré que : $\pu{3,125} \leqslant \sqrt{10} \leqslant \pu{3,25}$.
-
Avec quelques étapes de plus, on obtient :
| $a_0=3$ | $b_0=4$ |
| $a_1=3$ | $b_1=\pu{3,5}$ |
| $a_2=3$ | $b_2=\pu{3,25}$ |
| $a_3=\pu{3,125}$ | $b_3=\pu{3,25}$ |
| $a_4=\pu{3,125}$ | $b_4=\pu{3,1875}$ |
| $a_5=\pu{3,15625}$ | $b_5=\pu{3,1875}$ |
| $a_6=\pu{3,15625}$ | $b_6=\pu{3,171875}$ |
| $a_7=\pu{3,15625}$ | $b_7=\pu{3,164062}$ |
| $a_8=\pu{3,16015}$ | $b_8=\pu{3,164062}$ |
En 8 étapes, on obtient donc l’encadrement : $$\pu{3,160} \leqslant \sqrt{10} \leqslant \pu{3,165}$$ ce qui donne les deux premières décimales du résultat.
Nombre d’itérations nécessaires pour atteindre un résultat
La longueur de l’intervalle $[a_n, b_n]$ est $\dfrac{b - a}{2^n}$ puisqu’il a été nécessaire de découper $n$ fois l’intervalle de départ en deux pour parvenir à cet intervalle.
On peut alors rechercher le nombre d’itérations nécessaires pour atteindre une précision choisie lors de la phase préliminaire de l’étude ; il suffit de rechercher le nombre $n$ tel que $\dfrac{b - a}{2^n} \leqslant 10^{- N}$ :
$$ (b - a) 10^N \leqslant 2^n $$
$$ \log (b - a) + \log (10^N) \leqslant \log (2^n) $$
$$ \log (b - a) + N \leqslant n \log (2) $$
$$ n \geqslant \dfrac{\log (b - a) + N}{\log (2)} $$
Exemple. $\log (2) \simeq \pu{0,3} \iff \dfrac{1}{\log (2)} = \pu{3,3}$ donc si $\log (b - a) \leqslant 1$, une précision de :
-
$10^{- 10}$ ($\thicksim$ 10 décimales) nécessite 34 itérations ;
-
$10^{- 100}$ ($\thicksim$ 100 décimales) nécessite 333 itérations ;
-
$10^{- 1000}$ ($\thicksim$ 1000 décimales) nécessite 3322 itérations.
Ajouter une décimale nécessite donc 3 ou 4 itérations supplémentaires.
Implémentation en Python de l’algorithme
L’objectif de cette partie pratique est de mettre en œuvre la méthode de dichotomie en Python pour rechercher la racine carré de 10.
Utiliser un algorithme itératif puis un algorithme récursif.