Problème de la sous-séquence de somme maximale

Ce document étudie le problème de la sous-séquence de somme maximale. Ce problème est intéressant parce qu’il existe nombre d’algorithmes pour le résoudre et la complexité (en nombre d’opérations de somme) de ces algorithmes varie considérablement. Seulement deux algorithmes seront abordés, un prochain document présentera l’algorithme le plus efficace (cf. programmation dynamique).

Présentation

Exemples

• Pour le tableau tab = [-2, -5, 6, -2, -3, 1, 5, -6], la sous séquence de somme maximale est [6, -2, -3, 1, 5] et sa somme est 7.
• Pour le tableau tab = [0, 1, 2, -2, 3, 2], la sous séquence de somme maximale est [1, 2, -2, 3, 2] et sa somme est 6.
• Pour le tableau tab = [1, -2, 3, 10, -4, 7, 2, -5], la sous séquence de somme maximale est [3, 10, -4, 7, 2] et sa somme est 18.

Paradigme « Brute force »

1. On envisage dans un premier temps un algorithme basé sur le paradigme « Brute force » : on évalue la somme de chaque sous-tableau (parmi les $n(n + 1)/2$ sous-tableaux possibles) et à chaque évaluation on mémorise la somme maximale. Écrire le code de la fonction sous_tab_max dont la spécification est :

1
2
3
4
5
6

def sous_tab_max(tab: List[int]) -> int:
    """
    Recherche de la somme maximale dans un tableau.
    
    Paradigme : « Brute force ».
    """

Tester cette fonction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def sous_tab_max(tab: List[int]) -> int:
    """
    Recherche de la somme maximale dans un tableau.
    
    Paradigme : « Brute force ».
    """
    smax = 0
    for i in range(len(tab) - 1):
        somme = 0
        for j in range(i, len(tab)):
            somme += tab[j]
            smax = max(smax, somme)
    return smax

2. Quelle est la complexité de cette fonction ?

Paradigme « Diviser pour régner »

Dans la suite, on cherche à mettre en œuvre le paradigme « Diviser pour régner ».

Le tableau initial est scindé en deux parties de tailles à peu près égales (selon que $n$ est pair ou impair) : la plus grande somme se trouve soit dans le sous-tableau $B$ de droite, soit dans le sous-tableau $A$ de gauche, soit à cheval sur les deux sous-parties. Dans ce dernier cas elle est constituée d’une plus grande somme de la partie gauche se terminant à la fin de la partie gauche (c.-à-d. en $m$), et d’une plus grande somme de la partie droite commençant au début de la partie droite (c’est à dire en $m+1$).

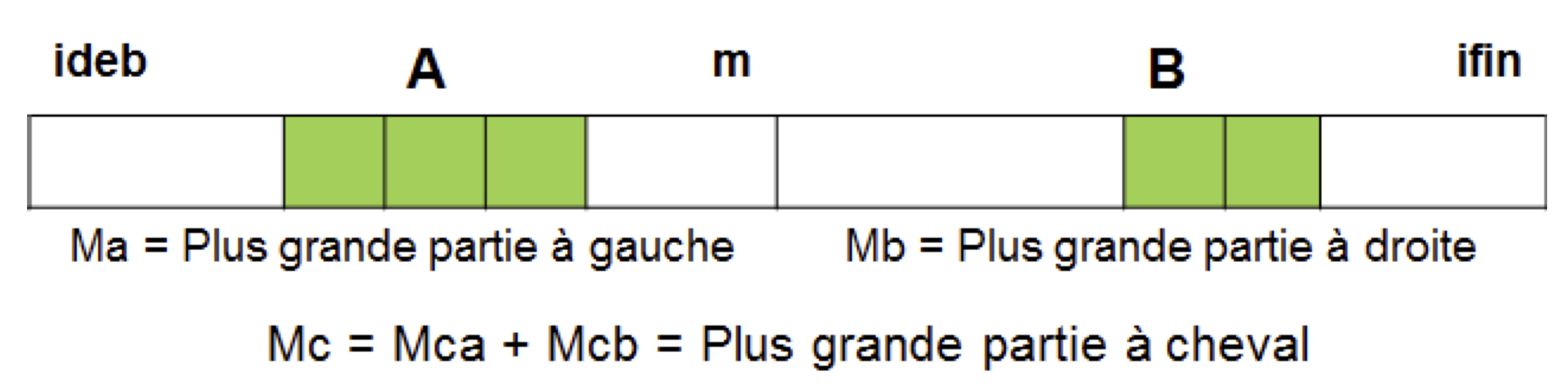
La procédure est récursive. Pour « sortir » des appels récursifs, il est nécessaire de rencontrer un « couple de données-paramètres » (transmis à l’appel) dont la solution est triviale. C’est le cas si le tableau est composé d’au plus un élément.

3. Écrire le code de la fonction somme_max dont la spécification est :

1
2
3
4
5
6

def somme_max(tab: List[int]) -> int:
    """
    Recherche de la somme maximale dans un 
    sous-tableau en appliquant le paradigme
    « Diviser pour régner ».
    """

Remarque

Ne pas effectuer le calcul de la somme maximale se trouveant dans la séquence à cheval sur les deux sous-parties. Ce calcul doit être effectué par un appel à la fonction max_sous_tab définie ci-dessous.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def somme_max(tab: List[int]) -> int:
    """
    Recherche de la somme maximale dans un 
    sous-tableau en appliquant le paradigme
    « Diviser pour régner ».
    """
    # Cas de base
    if len(tab) == 1:
        return max(0, tab[0])

    # Diviser
    milieu = len(tab) // 2

    s_max1 = somme_max(tab[:milieu])
    s_max2 = somme_max(tab[milieu:])
    s_max3 = max_sous_tab(tab, milieu)

    # Régner
    s_max = max(s_max1, s_max2, s_max3)

    # Combiner
    return s_max

4. Écrire le code de la fonction max_sous_tab dont la spécification est :

1
2
3
4
5

def max_sous_tab(tab: List[float], milieu: int) -> float:
    """
    Recherche la somme maximale entre les deux
    sous-tableaux du tableau tab à partir du milieu.
    """

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

def max_sous_tab(tab: List[float], milieu: int) -> float:
    """
    Recherche la somme maximale entre les deux
    sous-tableaux du tableau tab à partir du milieu.
    """
    # Sous-tableau gauche
    gmax = 0
    somme = 0
    for i in range(milieu, -1, -1):
        somme += tab[i]
        gmax = max(gmax, somme)
    # Sous-tableau droit
    dmax = 0
    somme = 0
    for i in range(milieu + 1, len(tab)):
        somme += tab[i]
        dmax = max(dmax, somme)
    return gmax + dmax

5. Quelle est la complexité de la fonction somme_max ?