Évolution d’un système chimique
Un système chimique évolue tant que les quantités de matière des réactifs (et donc des produits) changent macroscopiquement.
L’évolution d’un système chimique peut conduire à deux situations différentes :
-
Dans l’état final, au moins un des réactifs a disparu : la transformation chimique est alors dite totale.
-
Dans l’état final, aucun des réactifs n’a totalement disparu mais le système chimique a atteint un état d’équilibre chimique : la transformation chimique est alors dite limitée et l’état final est un état d’équilibre.
Mélange dans les proportions stœchiométriques
Exercice 1. Réaction du monoxyde de carbone et du dioxygène
Le monoxyde de carbone $\ce{CO}$ peut réagir avec le dioxygène pour former du dioxyde de carbone.
- Écrire l’équation de cette réaction en utilisant les nombres stœchiométriques entiers les plus petits possibles.
Réponse
$$ \ce{ CO (g) + 1/2 O2 (g) –> CO2 (g) } $$ donc $$ \ce{ 2 CO (g) + O2 (g) –> 2 CO2 (g) } $$
- Quelle quantité de matière de dioxygène est nécessaire pour faire réagir 2 moles de monoxyde de carbone ? Pour faire réagir 6 moles de monoxyde de carbone ?
Réponse
D’après l’équation de la réaction, $$ \dfrac{n(\ce{CO})_{\text{qui réagit}}}{n (\ce{O2})_{\text{qui réagit}}} = \dfrac{2}{1} \iff n (\ce{O2})_{\text{qui réagit}} = \dfrac{1}{2} n(\ce{CO})_{\text{qui réagit}} $$
A.N. $n (\ce{O2})_{\text{qui réagit}} = \dfrac{1}{2} \times \pu{2 mol} = \pu{1mol}$.
Pour faire réagir $\pu{2 mol}$ de monoxyde de carbone, il faut $\pu{1 mol}$ de dioxygène. On voit immédiatement qu’il faut $\pu{3 mol}$ de dioxygène pour faire réagir $\pu{6 mol}$ de monoxyde de carbone.
- Quelle quantité de matière de dioxyde de carbone obtient-on lorsqu’on fait réagir 3 moles de monoxyde de carbone ?
Réponse
D’après l’équation de la réaction, $$ \dfrac{n(\ce{CO})_{\text{qui réagit}}}{n (\ce{CO2})_{\text{qui se forme}}} = \dfrac{2}{2} = 1 \iff n (\ce{CO2})_{\text{qui se forme}} = n(\ce{CO})_{\text{qui réagit}} $$
A.N. $n (\ce{CO2})_{\text{qui se forme}} = \pu{3 mol} $
- Déterminer l’expression littérale indiquant quelles sont « les proportions données par les nombres stœchiométriques » pour la réaction étudiée dans cet exercice.
Réponse
$$ \dfrac{n(\ce{CO})_{\text{qui réagit}}}{2} = \dfrac{n (\ce{O2})_{\text{qui réagit}}}{1} = \dfrac{n (\ce{CO2})_{\text{qui se forme}}}{2} $$
Exercice 2. Synthèse du nitrobenzène
Le nitrobenzène $\ce{C6H5NO2}$ est utilisé dans la chimie des colorants. On le prépare par action de l’acide nitrique $\ce{HNO3}$ sur le benzène $\ce{C6H6}$.
- Écrire l’équation de cette réaction en utilisant les nombres stœchiométriques entiers les plus petits possibles sachant qu’il se forme aussi de l’eau.
Réponse
$$ \ce{ HNO3 + C6H6 –> C6H5NO2 + H2O } $$
- On met en présence 2 moles d’acide nitrique et 3 moles de benzène. Le mélange ainsi formé est-il dans les proportions stœchiométriques ?
Réponse
Pour que le mélange soit préparé dans les proportions stœchiométriques, il faut que $$ \dfrac{n_0 (\ce{HNO3})}{1} = \dfrac{n_0 (\ce{C6H6})}{1} $$ ce qui n’est pas le cas ici puisque $\pu{2 mol} \neq \pu{3 mol}$.
Exercice 3. Combustion du propane
On considère la combustion complète du propane $\ce{C3H8}$ dans l’air.
- Écrire l’équation de cette réaction en utilisant les nombres stœchiométriques entiers les plus petits possibles.
Réponse
$$ \ce{ C3H8 (g) + 5 O2 (g) –> 3 CO2 (g) + 4 H2O (g) } $$
- On met en présence 2 moles de propane et 3 moles de dioxygène. Le mélange ainsi formé est-il dans les proportions stœchiométriques ?
Réponse
Pour que le mélange soit préparé dans les proportions stœchiométriques, il faut que $$ \ce{ \dfrac{n_0 (\ce{C3H8})}{1} = \dfrac{n_0 (\ce{O2})}{5} } $$ ce qui n’est pas le cas ici puisque $\pu{2 mol} \neq \dfrac{\pu{3 mol}}{5} = \pu{0,6 mol}$.
Transformation chimique totale
Ce réactif est alors appelé réactif limitant.
Exercice 4. Obtention du soufre
L’une des étapes de la synthèse de l’acide sulfurique est la réaction entre le sulfure d’hydrogène $\ce{H2S}$ et le dioxyde de soufre $\ce{SO2}$. Le soufre $\ce{S}$ et l’eau sont les produits de cette réaction.
- Écrire l’équation de cette réaction en utilisant les nombres stœchiométriques entiers les plus petits possibles.
Réponse
$$ \ce{ \ce{H2S} + 1/2 \ce{SO2} –> 3/2 S + H2O } $$
-
On considère un état initial constitué de 4,0 moles de dioxyde de soufre et 5,0 moles de sulfure d’hydrogène.
Déterminer, à l’aide d’un tableau d’avancement :-
L’avancement maximal de la réaction et le réactif limitant.
-
La composition du système lorsque l’avancement est égal à la moitié de l’avancement maximal.
-
La composition de l’état final.
-
Réponse
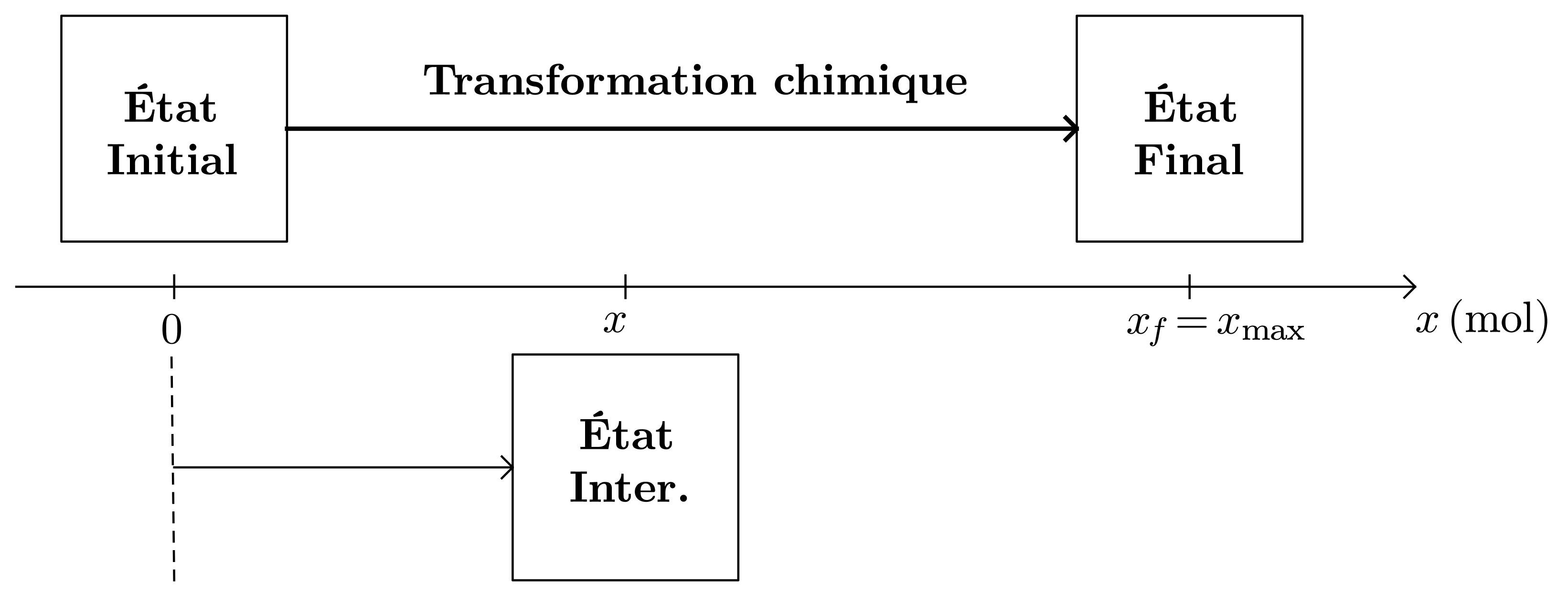
| État | Avancement | $\ce{2 H2S}$ | $+$ | $\ce{SO2}$ | $\ce{–>}$ | $\ce{3 S}$ | $+$ | $\ce{2 H2O}$ |
|---|---|---|---|---|---|---|---|---|
| Initial | 0 | $n_0(\ce{H2S})$ | $n_0(\ce{SO2})$ | $0$ | 0 | |||
| Intermédiaire | $x$ | $n_0(\ce{H2S})-2x$ | $n_0(\ce{SO2})-x$ | $3x$ | $2x$ | |||
| Final | $x_f=x_{\text{max}}$ | $n_0(\ce{H2S})-2x_{\text{max}}$ | $n_0(\ce{SO2})-x_{\text{max}}$ | $3x_{\text{max}}$ | $2x_{\text{max}}$ |
-
Le milieu contient du sulfure d’hydrogène tant que : $$ n (\ce{H2S}) \geqslant 0 \iff n_0 (\ce{H2S}) - 2 x \geqslant 0 \iff x \leqslant \dfrac{n_0 (\ce{H2S})}{2} $$
A.N. $x \leqslant \dfrac{\pu{5,0 mol}}{2} = \pu{2,5 mol}$.
Le milieu contient du dioxyde de soufre tant que : $$ n (\ce{SO2}) \geqslant 0 \iff n_0 (\ce{SO2}) - x \geqslant 0 \iff x \leqslant n_0 (\ce{SO2}) $$
A.N. $x \leqslant \pu{4,0 mol} $.
- Le sulfure d’hydrogène disparaît en premier ; c’est le réactif limitant.
- $x_{\text{max}} = \pu{2,5 mol}$
-
Pour $\pu{x = 1,25 mol}$,
-
$n (\ce{H2S}) = n_0 (\ce{H2S}) - 2 x = \pu{5,0 mol} - 2 \times \pu{1,25 mol} = \pu{2,5 mol}$
-
$ n (\ce{SO2}) = n_0 (\ce{SO2}) - x = \pu{4,0 mol}- \pu{1,25 mol} = \pu{2,75 mol} $
-
$ n (\ce{S}) = 3 x = 3 \times \pu{1,25 mol} = \pu{3,75 mol} $
-
$ n (\ce{H2O}) = 2 x = 2 \times \pu{1,25 mol} = \pu{2,50 mol} $
-
-
Dans l’état final,
-
$n_f(\ce{H2S}) = \pu{0 mol}$
-
$n (\ce{SO2}) = \pu{4 mol} - \pu{2,5 mol} = \pu{1,5 mol}$
-
$n (\ce{S}) = 3 \times \pu{2,5 mol} = \pu{7,5 mol}$
-
$n (\ce{H2O}) = 2 \times \pu{2,5 mol} = \pu{5,0 mol}$
-
-
On considère à présent un mélange initial contenant 3,5 moles de dioxyde de soufre et $n$ moles de sulfure d’hydrogène.
-
Déterminer la valeur de $n$ pour que le mélange initial soit dans les proportions stœchiométriques.
-
En déduire alors la composition de l’état final.
-
Réponse
-
Pour que le mélange soit préparé dans les proportions stœchiométriques, il faut $$ \dfrac{n_0 (\ce{H2S})}{2} = \dfrac{n_0 (\ce{SO2})}{1} \iff n_0 (\ce{H2S}) = 2 n_0 (\ce{SO2}) $$
A.N $n_0 (\ce{H2S}) = 2 \times \pu{3,5 mol} = \pu{7,0 mol}$
-
Dans l’état final,
-
$n (\ce{H2S}) = \pu{0 mol}$
-
$n (\ce{SO2}) = \pu{0 mol}$
-
$n (\ce{S}) = 3 \times \pu{3,5 mol} = \pu{10,5 mol}$
-
$n (\ce{H2O}) = 2 \times \pu{3,5 mol} = \pu{7,0 mol}$
Lorsque le mélange des réactifs est préparé dans les proportions stœchiométriques il ne reste aucun des réactifs dans l’état final.
-
Exercice 5. Obtention du monoxyde d’azote
La réaction de l’ammoniac $\ce{NH3}$ avec le dioxygène, pour donner de l’eau et du monoxyde d’azote $\ce{NO}$, est l’une des étapes de la synthèse industrielle de l’acide nitrique.
- Écrire l’équation de cette réaction en utilisant les nombres stœchiométriques entiers les plus petits possibles.
Réponse
$$ \ce{ NH3 + 5/4 O2 –> NO + 3/2 H2O } $$ donc $$ \ce{ 4 NH3 + 5 O2 –> 4 NO + 6 H2O } $$
-
L’état initial d’un système est constitué d’une masse $m_1 = \pu{340 g}$ d’ammoniac et d’une masse $m_2 = \pu{480 g}$ de dioxygène. Déterminer à l’aide d’un tableau d’avancement (lorsque nécessaire) :
-
Les quantités de matière d’ammoniac et de dioxygène dans le système à l’état initial.
-
L’avancement maximal de la réaction et le réactif limitant.
-
La composition, en quantités de matière, puis en masse, de l’état final du système.
-
Réponse
| État | Avancement | $\ce{4 NH3}$ | $+$ | $\ce{5 O2}$ | $\ce{–>}$ | $\ce{4 NO}$ | $+$ | $\ce{6 H2O}$ |
|---|---|---|---|---|---|---|---|---|
| Initial | 0 | $n_0(\ce{NH3})$ | $n_0(\ce{O2})$ | $0$ | $0$ | |||
| Intermédiaire | $x$ | $n_0(\ce{NH3})-4x$ | $n_0(\ce{O2})-5x$ | $4x$ | $6x$ | |||
| Final | $x_f=x_{\text{max}}$ | $n_0(\ce{NH3})-4x_{\text{max}}$ | $n_0(\ce{O2})-5x_{\text{max}}$ | $4x_{\text{max}}$ | $6x_{\text{max}}$ |
-
$n_0 (\ce{NH3}) = \dfrac{m_1}{M (\ce{NH3})}$
A.N. $n_0 (\ce{NH3}) = \dfrac{\pu{340 g}}{(\pu{14,0} + 3 \times \pu{1,0})\pu{g.mol-1}} = \pu{20,0 mol}$
$n_0 (\ce{O2}) = \dfrac{m_2}{M (\ce{O2})}$
A.N. $n_0 (\ce{O2}) = \dfrac{\pu{480 g}}{(2 \times \pu{16,0})\pu{g.mol-1}} = \pu{15,0 mol}$
-
Le système contient de l’ammoniac tant que $$ n (\ce{NH3}) \geqslant 0 \iff n_0 (\ce{NH3}) - 4 x \geqslant 0 \iff x \leqslant \dfrac{n_0 (\ce{NH3})}{4} $$
A.N. $x \leqslant \dfrac{\pu{20,0 mol}}{4} = \pu{5,0 mol}$
Le système contient du dioxygène tant que $$ n (\ce{O2}) \geqslant 0 \iff n_0 (\ce{O2}) - 5 x \geqslant 0 \iff x \leqslant \dfrac{n_0 (\ce{O2})}{5} $$
A.N. $x \leqslant \dfrac{\pu{15,0 mol}}{5} = \pu{3,0 mol}$
-
Le dioxygène disparaît en premier, c’est le réactif limitant.
-
$x_{\max} = \pu{3,0 mol}$.
-
-
Dans l’état final,
-
$n (\ce{NH3}) = \pu{20,0 mol} - 4 \times \pu{3,0 mol} = \pu{8,0 mol}$
-
$n (\ce{O2}) = \pu{0 mol}$
-
$n (\ce{NO}) = 4 \times \pu{3,0 mol} = \pu{12,0 mol}$
-
$n(\ce{H2O}) = 6 \times \pu{3,0 mol} = \pu{18,0 mol}$
Calcul des masses finales,
-
$m (\ce{NH3}) = \pu{8,0 mol} \times (\pu{14,0} + 3 \times \pu{1,0})\pu{g.mol-1} = \pu{136 g}$
-
$m(\ce{NO}) = \pu{12,0 mol} \times (\pu{14,0} + \pu{16,0})\pu{g.mol-1} = \pu{360 g}$
-
$m (\ce{H2O}) = \pu{18,0 mol} \times (2 \times \pu{1,0} + \pu{16,0})\pu{g.mol-1} = \pu{324 g}$
-
- Déterminer la masse $m’$ du réactif limitant qu’il aurait fallu utiliser pour obtenir un mélange initial stœchiométrique, la masse de l’autre réactif restant identique.
Réponse
Pour que le mélange initial soit préparé dans les proportions stœchiométriques, on doit avoir : $$ \dfrac{n_0 (\ce{NH3})}{4} = \dfrac{n_0 (\ce{O2})}{5} \iff n_0 (\ce{O2}) = \dfrac{5}{4} n_0 (\ce{NH3}) $$
A.N. $n_0 (\ce{O2}) = \dfrac{5}{4} \times \pu{20,0 mol} = \pu{25,0 mol}$.
Il aurait donc fallu introduire, $m_0 (\ce{O2}) = \pu{25,0 mol} \times (2 \times \pu{16,0 g.mol-1}) = \pu{800 g}$.
- Comparer la masse du système dans l’état final et dans l’état initial à l’aide des résultats de la question 2.3.
Réponse
-
État initial :
$m_0 (\ce{NH3}) + m_0 (\ce{O2}) + m_0 (\ce{NO}) + m_0 (\ce{H2O}) = \pu{340 g} + \pu{480 g} = \pu{820 g}$ -
État final :
$m_f (\ce{NH3}) + m_f (\ce{O2}) + m_f (\ce{NO}) + m_f (\ce{H2O}) = \pu{136 g} + \pu{360 g} + \pu{324 g} = \pu{820 g}$
La masse totale du système est conservée lors d’une transformation chimique.
Exercice 6. Combustion de l’aluminium
Le métal aluminium Al brûle dans le dioxygène pour donner de l’alumine $\ce{Al2O3}$ solide.
- Donnée
-
À 0 C, $V_m = \pu{22,4 L.mol-1}$, à 20 C, $V_m = \pu{24,1 L.mol-1}$.
-
Écrire l’équation de cette réaction en utilisant les nombres stœchiométriques entiers les plus petits possibles.
-
On souhaite brûler complètement 0,54 g d’aluminium dans du dioxygène. Déterminer le volume de dioxygène nécessaire et la masse d’alumine formée.
-
On souhaite à présent obtenir par cette réaction une masse d’alumine $m (\ce{Al2O3}) = \pu{30,6 g}$. Déterminer :
-
Les quantités de matière de dioxygène et d’aluminium nécessaires.
-
La masse d’aluminium et le volume de dioxygène correspondants.
-
Une transformation chimique n’est pas toujours totale
-
Une transformation chimique est limitée (non totale) si, dans l’état final aucun des réactifs n’a complètement disparu.
-
L’avancement final d’une transformation chimique limitée est inférieur à l’avancement maximal, avancement d’une transformation chimique totale hypothétique à partir du même système chimique. $$x_f < x_{\text{max}}$$
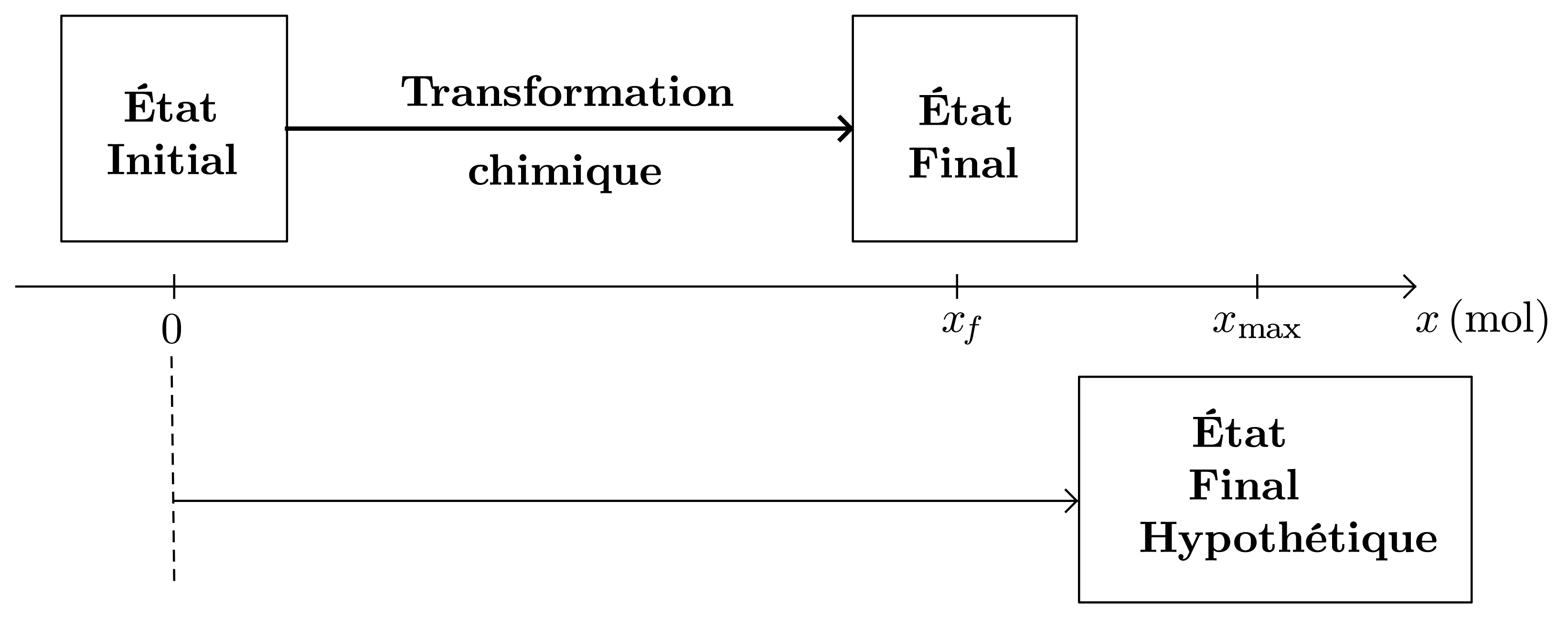> L'état final hypothétique correspond à l'état qu'atteindrait le système **si la transformation chimique était totale**.
Exercice 7. Synthèse commerciale de l’urée
L’urée est une importante matière première pour l’industrie chimique : synthèse d’engrais ou de plastiques, alimentation animale, réduction de polluants, etc. Pour le synthétiser au laboratoire, on introduit une quantité $n_1 = \pu{1,0 mol}$ de dioxyde de carbone et $n_2 = \pu{2,0 mol}$ d’ammoniac $\ce{NH3}$.
On obtient $n_3 = \pu{0,39 mol}$ d’eau et $n_4 = \pu{0,39 mol}$ d’urée $\ce{CON2H4}$.
- Écrire l’équation de la réaction avec les nombres stœchiométriques entiers les plus petits possibles.
Réponse
- Comment peut-on qualifier le mélange initial ?
Réponse
- Déterminer la valeur de l’avancement final $x_f$.
Réponse
- Déterminer la valeur de l’avancement maximal $x_{\text{max}}$.
Réponse
- Comparer $x_f$ et $x_{\text{max}}$. Quelle conclusion peut-on tirer du résultat de cette comparaison ?