Formation d'une image à l'aide d'une lentille mince convergente

Lentille

Une lentille est constituée d’un matériau transparent limité par deux surfaces sphériques ou une surface sphérique et une surface plane. Elle possède un axe de symétrie appelé axe optique. À chacune de ses surfaces la lumière est réfractée.

Une lentille réfracte donc la lumière deux fois :

  • à l’interface air - matériau (lorsque la lumière entre dans la lentille) ;
  • à l’interface matériau - air (lorsque la lumière sort de la lentille). En fonction de la forme de la surface de la lentille, la lumière est réfractée différemment.

Objet et image

Une lentille donne d’un objet une image dont la position et la taille dépendent de la distance fixée entre l’objet et la lentille.

Précisons la définition d’un objet et d’une image.

Point objet et objet

Un point objet est l’intersection des rayons incidents, c’est à dire des rayons lumineux qui arrivent sur un système optique (lentille, association de lentilles, miroirs, etc.).

Deux situations sont à envisager :

  • le point objet est à distance finie du système optique, les rayons incidents (ou leurs prolongements) se coupent.
  • le point objet est très éloigné du système optique, il est dit à l’infini, les rayons incidents sont parallèles.

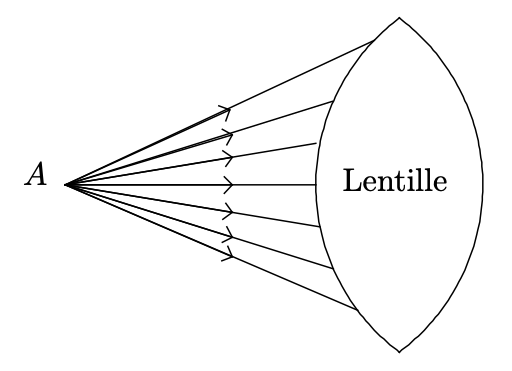
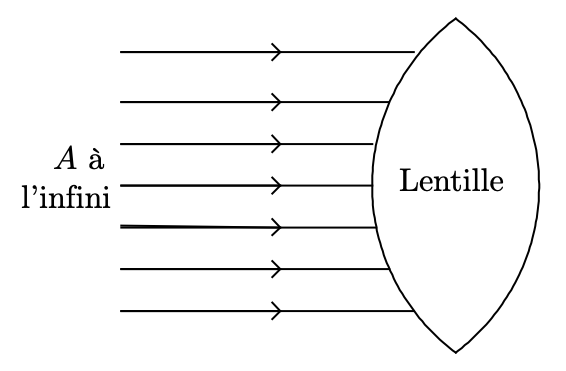
Point objet à distance finie et point objet à distance infinie.

L’objet est modélisé comme un ensemble de points objets.

Point image et image

Un point image est l’intersection des rayons émergents, c’est-à-dire des rayons lumineux qui quittent le système optique.

Deux situations sont à envisager :

  • le point image est à distance finie du système optique, les rayons émergents ou leurs prolongements se coupent.
  • le point image est très éloigné du système optique , il est dit à l’infini : les rayons émergents sont parallèles.

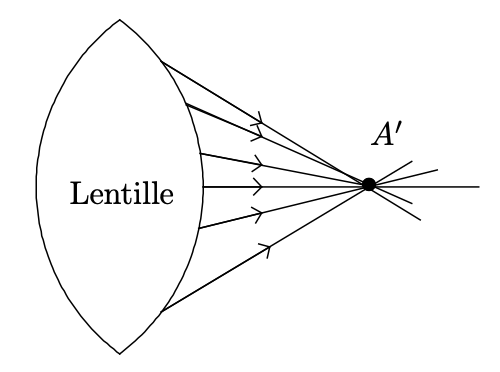
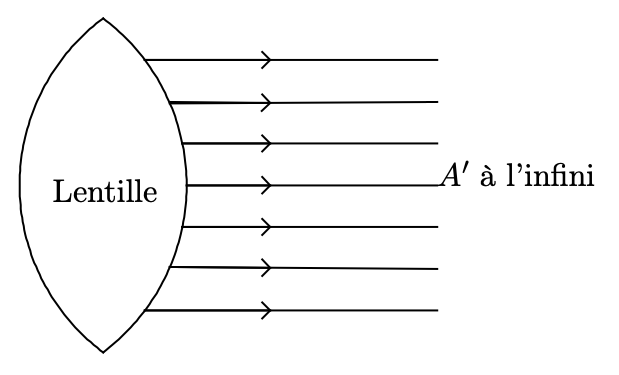
Point image à distance finie et point objet à distance infinie.

L’image de l’objet est l’ensemble des points images.

Le modèle des lentilles minces convergentes

Manipulations

Matériel : Une source lumineuse munie d’une grille, des lentilles convergentes de démonstration.

  • Diriger les pinceaux lumineux parallèlement à l’axe de la lentille (figure ci-dessous).
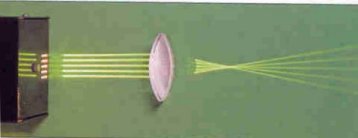
  1. La lentille est dite convergente. Justifier ce qualificatif.
Réponse

Les rayons de lumière qui arrivent parallèlement les uns aux autres convergent au-delà de la lentille.

  1. Existe-t-il des lentilles qui ne sont pas convergentes ? Comment peut-on reconnaître les lentilles convergentes parmi toutes les lentilles ?
Réponse

  • Il existe des lentilles divergentes : les rayons de lumière qui arrivent parallèlement les uns aux autres divergent au-delà de la lentille.

  • Les lentilles convergentes possèdent un bord mince alors que les lentilles divergentes possèdent un bord épais.

  1. L’image ci-dessus permet de visualiser le foyer image $F’$ de la lentille. Donner la définition de ce point.
Réponse
Le foyer image $F’$ est le lieu de convergence des rayons de lumière qui arrivent sur la lentille parallèlement à l’axe optique.
À l’aide d’une lentille auxilaire, créer un point objet pour la lentille étudiée et placer cette lentille de telle sorte que les rayons issus de ce point objet émergent de la lentille étudiée parallèlement à l’axe optique.
  1. Quel nom porte ce point objet ?
Réponse

C’est le foyer objet $F$.

  1. Où se situe la lentille par rapport aux deux foyers ?
Réponse

La lentille se trouve au milieu du segment $[F, F’]$.

  1. Compléter le schéma en indiquant la position des deux foyers.
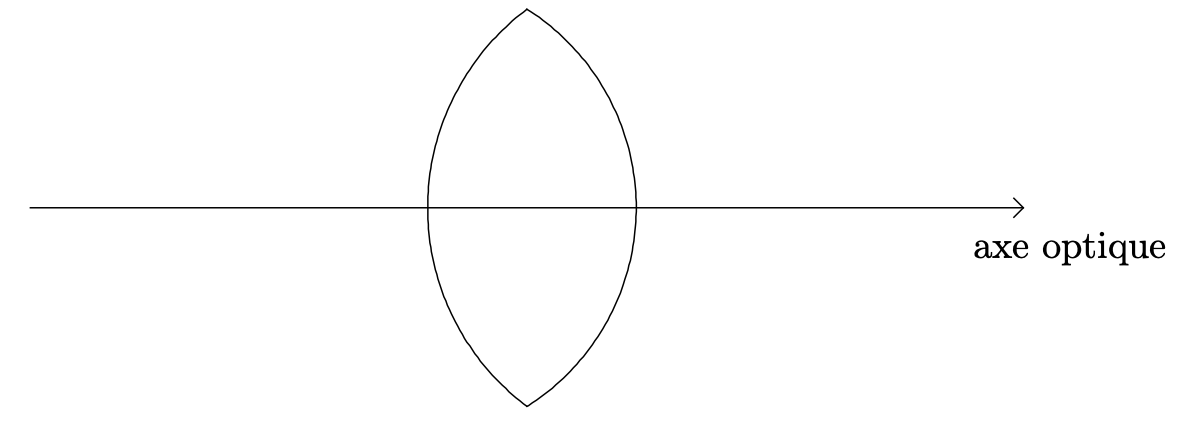
  1. Reprendre le dispositif de la figure ci-dessus et faire pivoter la lentille de façon à mettre en évidence l’existence d’un pinceau lumineux particulier qui n’est que très peu dévié. Par quel point particulier de la lentille passe ce pinceau lumineux ?
Réponse

Le pinceau lumineux passe par le centre de la lentille.

  1. Envisager le cas où l’épaisseur de la lentille est très faible et placer le point sur le schéma de la question 6.

Modélisation d’une lentille convergente

Si une lentille convergente est suffisamment mince, on peut négliger l’épaisseur de sa partie centrale qui se réduit alors à un point, noté $O$ et appelé centre optique. Dans ce cas, l’axe optique se confond avec la droite perpendiculaire à la lentille passant par $O$.
  1. Compléter la phrase suivante : Tout rayon passant par le centre optique : ……
Réponse
Tout rayon passant par le centre optique n’est pas dévié.

Foyer objet et foyer image

  1. Quelle propriété possède le foyer objet, point de l’axe, noté $F$ ?
Réponse
Le foyer objet est le point de l’axe, noté $F$, possédant la propriété suivante : Tout rayon incident passant par $F$ donne un rayon émergent parallèle à l’axe optique.
  1. Quelle propriété possède le foyer image, point de l’axe, noté $F’$ ?
Réponse
Le foyer image est le point de l’axe, noté $F’$, possédant la propriété suivante : Tout rayon incident parallèle à l’axe optique donne un rayon émergent qui passe par $F’$.
  1. Quelle particularité présentent $F$ et $F’$ par rapport au centre optique $O$ ?
Réponse
$F$ et $F’$ sont symétriques par rapport au centre optique $O$.

Distance focale et vergence

L’axe optique est orienté dans le sens de propagation de la lumière.

  • La distance focale, notée $f’$, est telle que : $$f’ = \overline{\operatorname{OF}’}$$ L’unité de la distance focale est le mètre (m). La distance focale est une mesure algébrique positive dans le cas des lentilles minces convergentes.
  • La vergence, notée $C$, est l’inverse de la distance focale : $$C = \frac{1}{\overline{\operatorname{OF}’}} = \frac{1}{f’}$$ L’unité de la vergence est la dioptrie ($\delta$).

Comment déterminer la position et de la taille d’une image ?

À l’aide d’une construction graphique

Par le calcul : relation de conjugaison

Relation entre les position de l’objet et de l’image

Placer l’objet lumineux, la lentille sur son support et l’écran sur le banc d’optique. Pour une distance fixée entre l’objet et la lentille, chercher la position de l’image en déplaçant l’écran. Mesurer alors la distance entre la lentille et l’écran. Effectuer ainsi 6 à 8 mesures et rassembler les mesures dans un tableau.

Résultats :

$\overline{OA\rq}$ (en m) $\overline{OA}$ (en m)
0,885 -0,250
0,543 -0,300
0,430 -0,350
0,379 -0,400
0,340 -0,450
0,312 -0,500
0,295 -0,550
  1. Représenter graphiquement $\dfrac{1}{\overline{OA\rq}}$ en fonction de $\dfrac{1}{\overline{OA}}$.

Relation de conjugaison

Une lentille mince de distance focale $f\rq$ donne d’un point objet $A$ situé sur l’axe optique, un point image $A\rq$ dont la position sur l’axe est donnée par la relation : $$\dfrac{1}{\overline{OA\rq}} - \dfrac{1}{\overline{OA}} = \dfrac{1}{f\rq}$$ $A$ et $A\rq$ sont dits conjugués.

Relation de grandissement

Les droites perpendiculaires à l’axe optique sont orientées positivement vers le haut.

Le grandissement noté $\gamma$ est le rapport de la taille de l’image et de la taille de l’objet : $$ \gamma = \dfrac{ \overline{A\rq B\rq} }{ \overline{A B} } $$

  • Lorsque $\gamma$ est positif, l’image est dite droite ;
  • Lorsque $\gamma$ est négatif, l’image est dite renversée.
  • Lorsque $\lvert \gamma \rvert > 1$, l’image est plus grande que l’objet.
  • Lorsque $\lvert \gamma \rvert < 1$, l’image est plus petite que l’objet.

Relation de grandissement dans le cas des lentilles minces convergentes

L’utilisation du théorème de Thales permet de montrer que, dans le cas particulier de la lentille mince convergente, on peut écrire : $$ \gamma = \dfrac{ \overline{A\rq B\rq} }{ \overline{A B} } = \dfrac{ \overline{OA\rq} }{ \overline{OA} }$$
Lentille mince convergente  Formation image  Geogebra  Rayons particuliers  Lentille  Lentille convergente  Distance focale  Foyer image  Foyer objet  Axe optique  Centre optique 

Suggestions de lecture :