Les effets de marée sont fréquemment cités. On les invoque, par exemple, pour expliquer la nature particulaire des anneaux de Saturne ou pour récuser telle hypothèse sur la formation des planètes.
Si l’on considère un point matériel, soumis aux seules actions gravitationnelles, son accélération $\vec{a} (M)$ au point $M$ relativement à un référentiel galiléen, est :
$$ \vec{a} (M) = \overrightarrow{G} (M) $$
où $\overrightarrow{G} (M)$ est le champ gravitationnel en $M$. De façon tout à fait extraordinaire, cette accélération est indépendante de la masse du corps ! C’est, sous une forme plus générale, la fameuse loi de chute des corps : dans le vide, tous les corps tombent également vite . Cette simplicité fondamentale est bien connue de tous, mais peut-être n’en tire-t-on pas suffisamment les conséquences. L’impesanteur est l’illustration évidente de la propriété précédente. Supposons, par exemple, un vaisseau spatial en mouvement sous l’action des seules forces gravitationnelles. Si le mouvement du vaisseau est une translation d’accélération $\vec{a}$ (relativement à un référentiel galiléen), dans un champ de gravitation uniforme $\overrightarrow{G}$, on a :
$$ \vec{a} = \overrightarrow{G} $$
Des objets de petites dimensions répartis dans le vaisseau spatial auront également la même accélération $\vec{a}$ quelle que soit leur nature . Ces objets apparaîtront donc à un observateur lié au vaisseau spatial comme n’ayant pas d’accélération : ils seront, relativement au vaisseau, immobiles ou en mouvement rectiligne uniforme (avec chocs possibles sur les parois du vaisseau dans ce dernier cas). L’astronaute interprète ce comportement en termes d’impesanteur. Cette impesanteur cesse dès que l’on applique au vaisseau une force supplémentaire $\vec{F}$ non gravitationnelle qui produit un supplément d’accélération du seul vaisseau égal à $\vec{F} / m$ ($m$ : masse du vaisseau). Supposons maintenant le champ $\overrightarrow{G}$ légèrement non uniforme, sa norme augmentant lorsqu’on passe de la région 1 (point $M_{1}$) à la région 2 (point $M_{2}$). Si l’on suppose encore le vaisseau animé d’un mouvement de translation, son accélération $\vec{a}_{v}$, est, avec une excellente approximation, égale à la valeur du champ gravitationnel au centre d’inertie $G$ du vaisseau, soit :
$$ \vec{a}_{v} \approx \overrightarrow{G} (G) $$
Un petit objet, situé en $M_{1}$, a l’accélération $\vec{a} (M_{1}) = \overrightarrow{G} (M_{1})$ et, de même, un objet situé en $M_{2}$ a l’accélération $\vec{a} (M_{2}) = \overrightarrow{G} (M_{2})$ (les accélérations étant mesurées dans un référentiel galiléen, cf. Figure 1). Relativement au vaisseau spatial, l’objet en $M_{1}$, a l’accélération :
$$ \vec{a}_{1} = \vec{a} (M_{1}) - \vec{a}_{v} \approx \overrightarrow{G} (M_{1}) - \overrightarrow{G} (G) $$
ll s’agit d’une accélération différentielle dirigée vers l’arrière du vaisseau, puisque :
$$ \lVert \overrightarrow{G} (M_{1}) \rVert < \lVert \overrightarrow{G} (G) \rVert $$
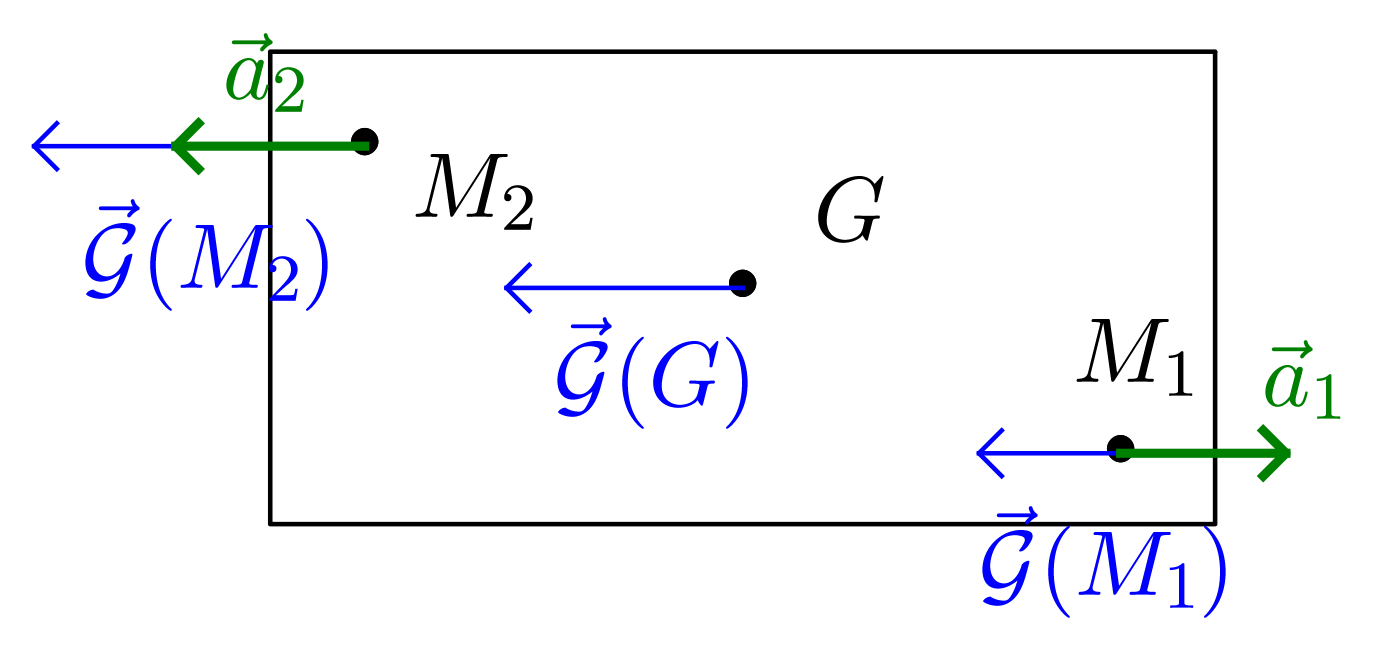
De même, l’objet en $M$, a l’accélération différentielle :
$$ \vec{a}_{2} = \vec{a} (M_{2}) - \vec{a}_{v} \approx \overrightarrow{G} (M_{2}) - \overrightarrow{G} (G) $$
dirigée vers l’avant du vaisseau.
On observe ainsi, du fait de la non-uniformité du champ de gravitation, des accélérations différentielles dirigées en sens opposés, d’où un effet de triage des objets. Il n’y a donc plus strictement impesanteur, les effets gravitationnels se manifestant — mais il est vrai de façon discrète —, puisqu’il s’agit d’effets différentiels. Le champ variant peu sur l’espace du vaisseau, ces termes différentiels restent cependant petits par rapport au champ gravitationnel lui-même.
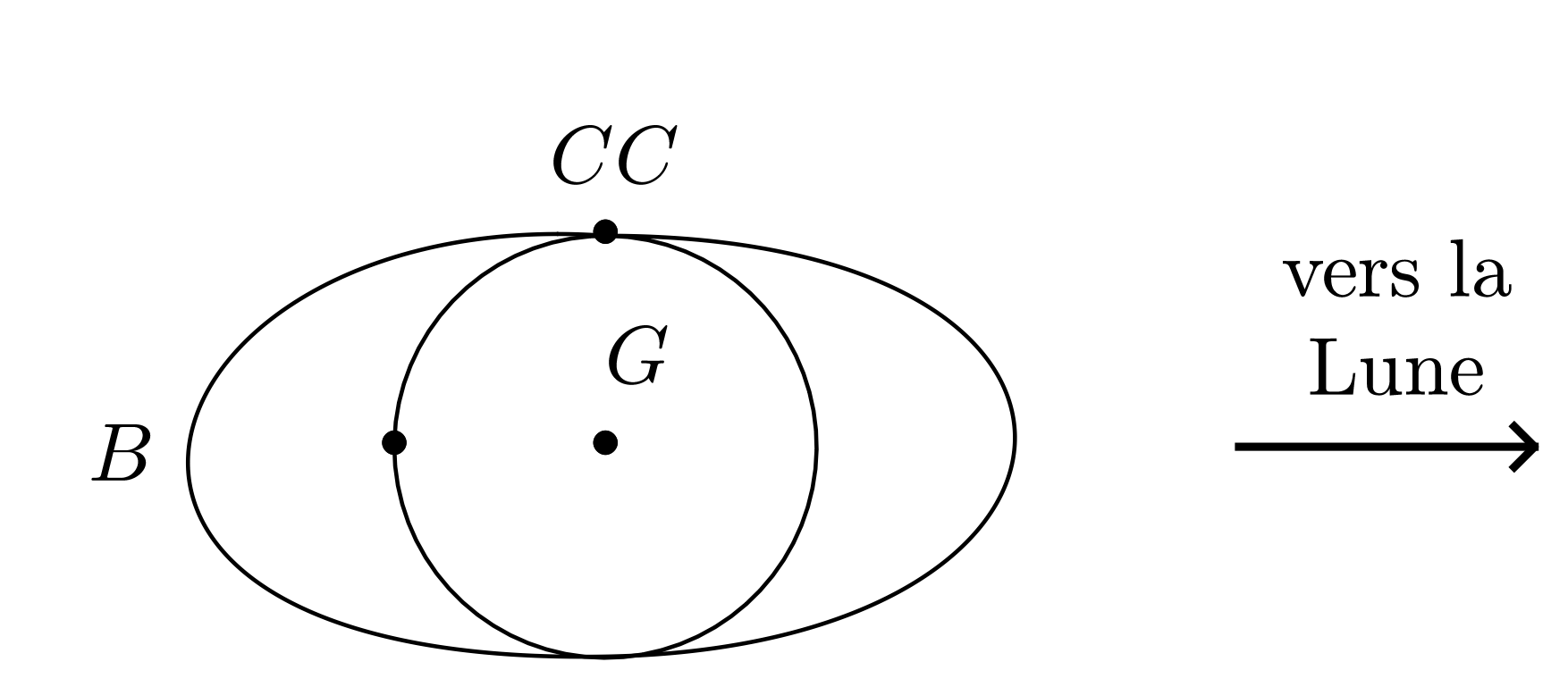
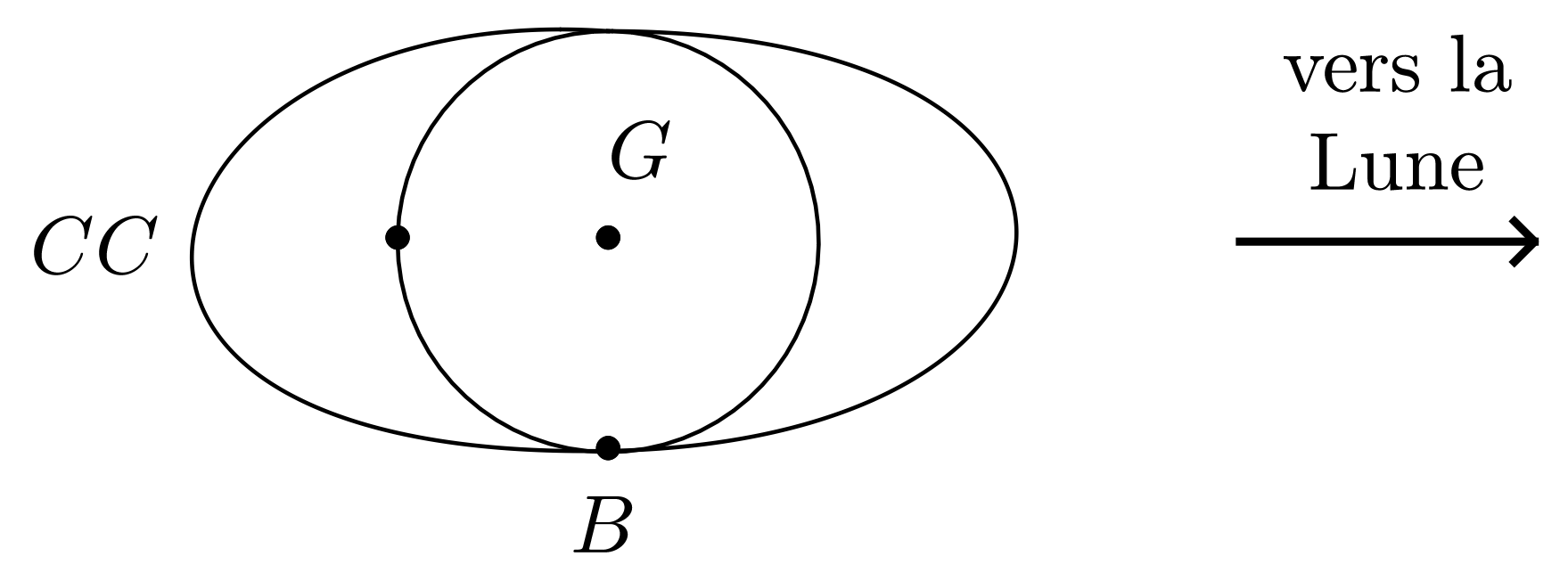
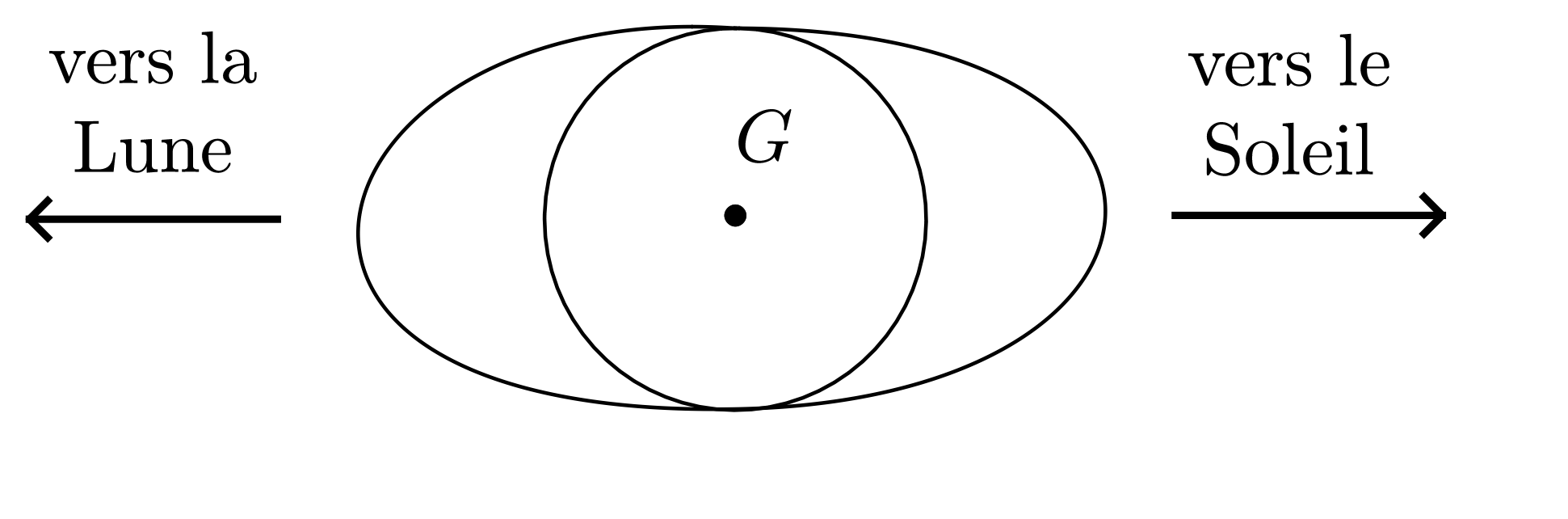
Le phénomène des marées s’explique par un effet différentiel du type précédent. La Terre (qui joue ici le rôle du vaisseau spatial) est plongée dans les champs de gravitation non uniformes de la Lune et du Soleil. Les éléments liquides des océans sont ainsi soumis à des accélérations différentielles de la forme :
$$ \overrightarrow{G} (M) - \overrightarrow{G} (G) $$
$M$ désignant la position de l’élément liquide considéré et $G$ le centre d’inertie de la Terre ; ces accélérations différentielles ne font intervenir en aucune manière les éléments liquides eux-mêmes. Seule compte leur position par rapport au centre d’inertie $G$ de la Terre.
Simplifions l’étude en considérant l’action d’un astre unique $A$ (Soleil ou Lune). Le champ gravitationnel créé par l’astre, soit $GM_{A} / r^2$, décroît du point $M_{1}$ au point $M_{2}$, d’où les directions en $M_{1}$ et $M_{2}$, des accélérations différentielles :
$$ \overrightarrow{G} (M_{1}) - \overrightarrow{G} (G) \text{ et } \overrightarrow{G} (M_{2}) - \overrightarrow{G} (G) $$
C’est un effet analogue à l’effet de triage indiqué plus haut. Le champ gravitationnel de l’astre $A$ n’intervient pas directement, mais se manifeste par des effets de différence dus à sa non-uniformité. Dans un champ uniforme, il n’y aurait pas de phénomène de marées !
Évaluons l’ordre de grandeur de cet effet. Si $r$ désigne la distance $\operatorname{AG}$ :
\[ G (G) = \frac{GM_{A}}{r^2} \]
\[ G (M_{1}) = \frac{GM_{A}}{(r - R)^2} \]
et
\[ G (M_{2}) = \frac{GM_{A}}{(r + R)^2} \]
où $R \ll r$ est le rayon de la Terre. On en déduit1 :
\[ | G (M_{2}) - G (G) | = | G (M_{1}) - G (G) | \approx \frac{2 GM_{A} R}{r^3} \]
soit
\[ | G (M_{2}) - G (G) | = | G (M_{1}) - G (G) | \approx 2 G (G) \frac{R}{r} \]
Pour le Soleil : $r = 1 {,} 5 \cdot 10^8 \text{km}$ ; prenons $R = 6 {,} 4 \cdot 10^3 \text{km}$. Le terme de marée a pour ordre de grandeur :
\[ G (G) \times \frac{2 \times 6 {,} 4 \cdot 10^3}{1 {,} 5 \cdot 10^8} \approx 8 {,} 5 \cdot 10^{- 5} \cdot G (G) \]
c’est-à-dire environ le 1/10 000 de la valeur du champ lui-même.
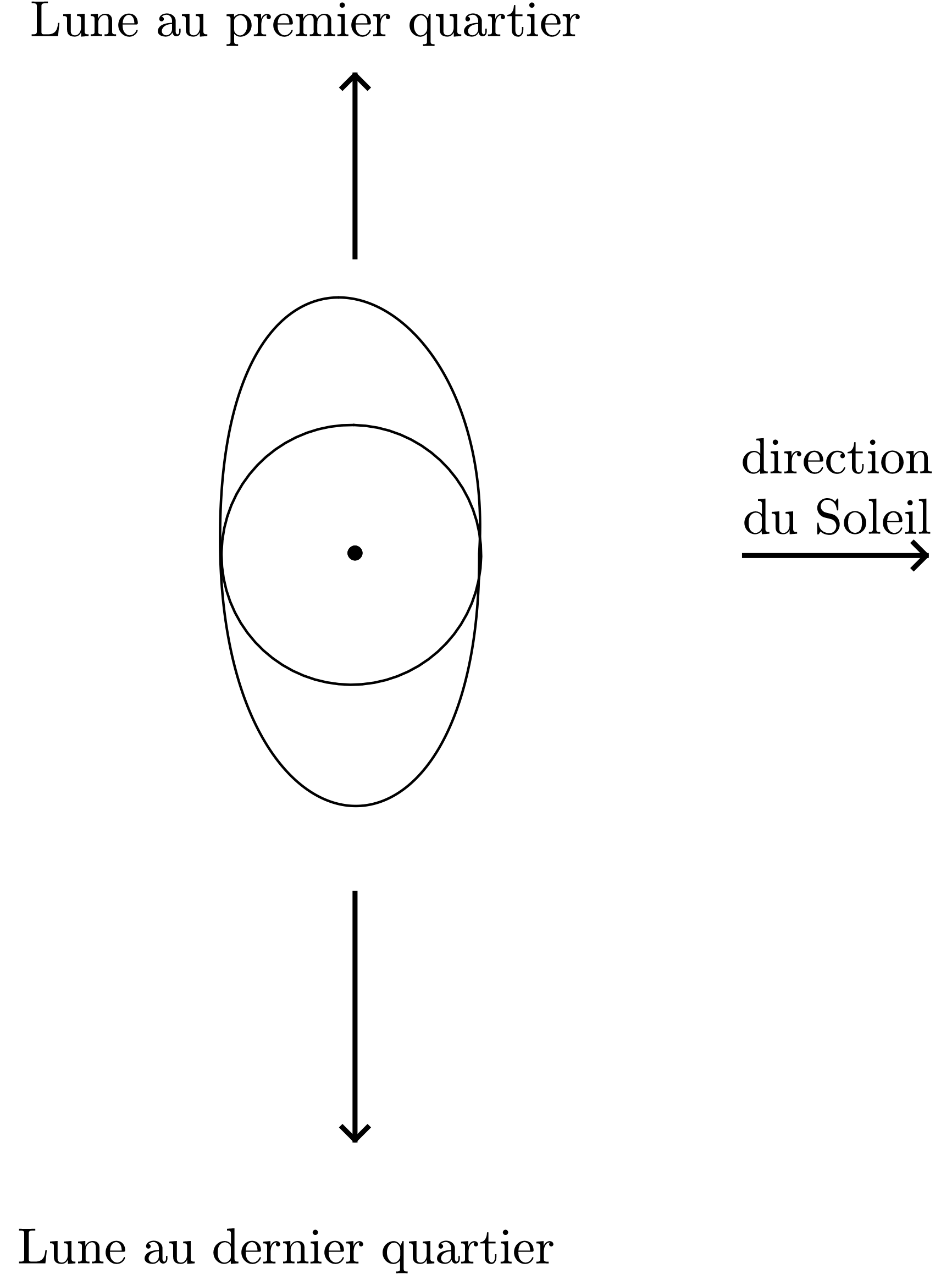
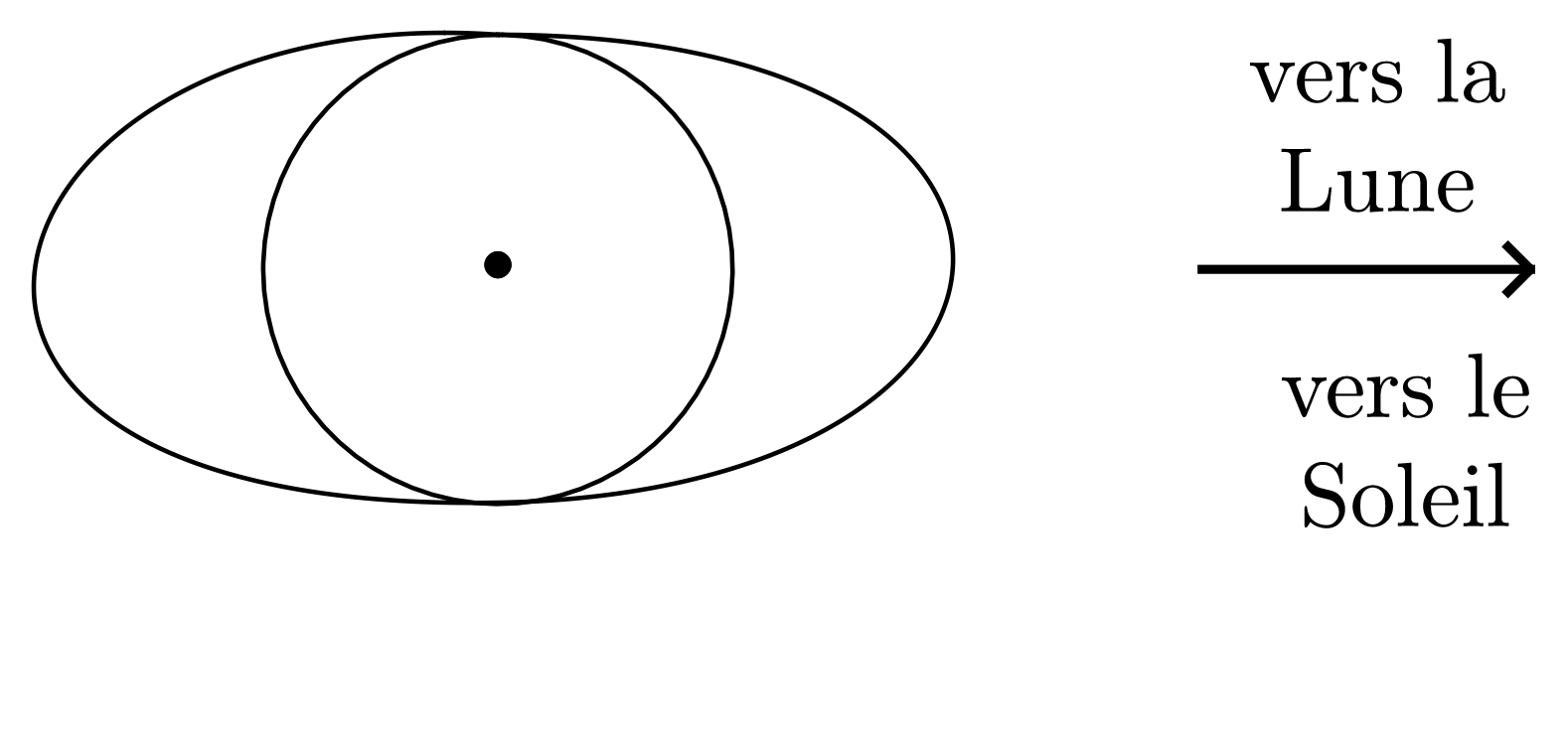
L’effet de marée a des effets visibles bien connus sur le mouvement des eaux des océans. L’étude complète du phénomène est d’ailleurs complexe, car il faut tenir compte de l’action simultanée du Soleil et de la Lune. En outre, interviennent des phénomènes d’amplification, on dit de résonance, du fait que les masses d’eau concernées peuvent être plus ou moins enfermées dans des cuvettes sous-marines.
On peut également noter que le globe terrestre lui-même n’est pas un solide tout à fait rigide. Les effets de marées se traduisent, de ce fait, par des déformations (très faibles) de notre globe. On explique aussi la constitution particulaire des anneaux de Saturne par effet de marée dans le champ (non uniforme) de la planète : des anneaux rigides seraient disloqués par cet effet de marée !
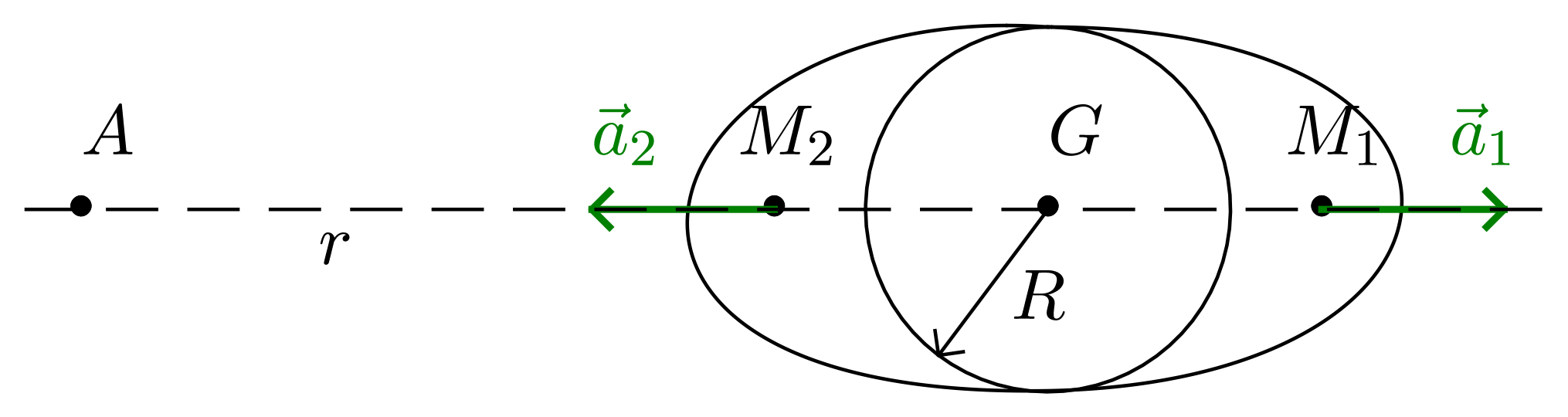
La théorie dite catastrophique de la formation des planètes de notre système solaire proposait l’éjection par le Soleil de globules planétaires sous l’effet d’une étoile perturbatrice. Une telle hypothèse doit, en fait, être rejetée. Un calcul simple montre, en effet, que sous l’action des effets de marée dus au champ solaire, de tels globules seraient disloqués dès leur formation au voisinage du Soleil.
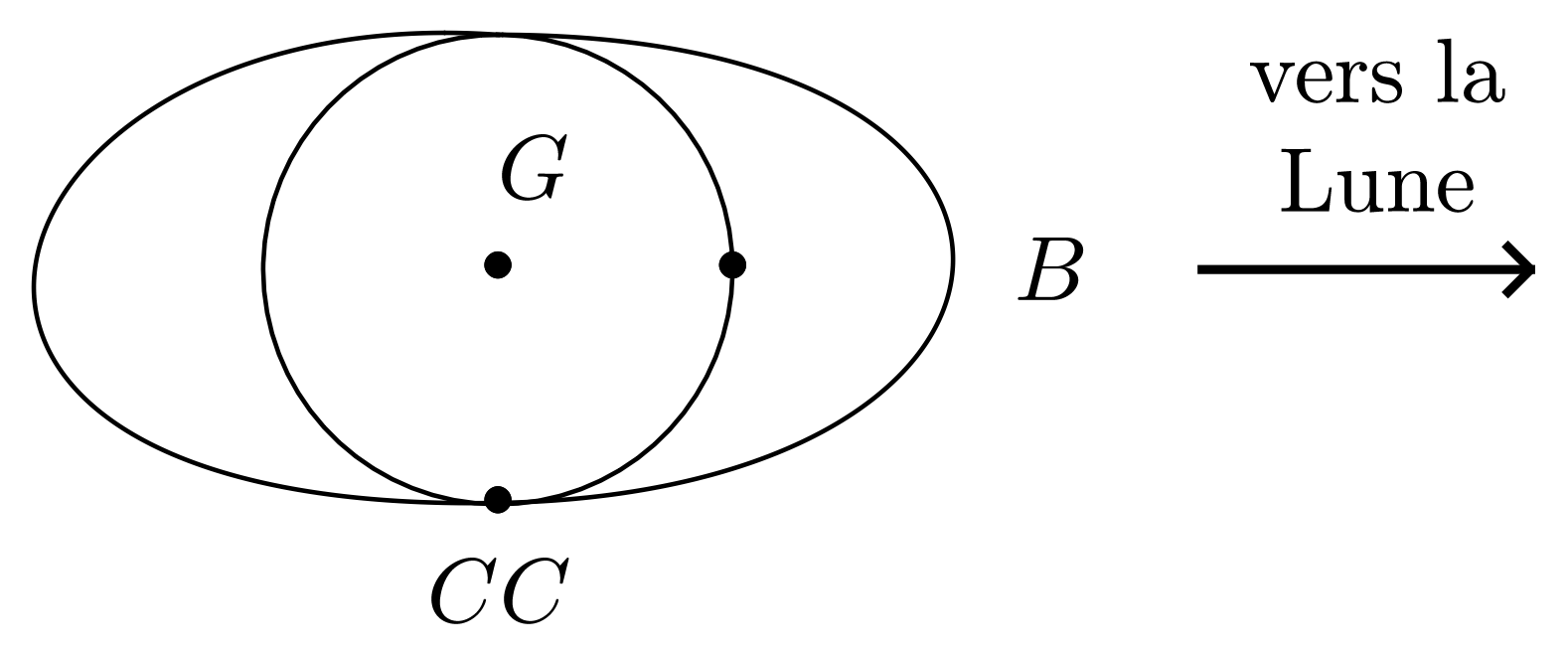
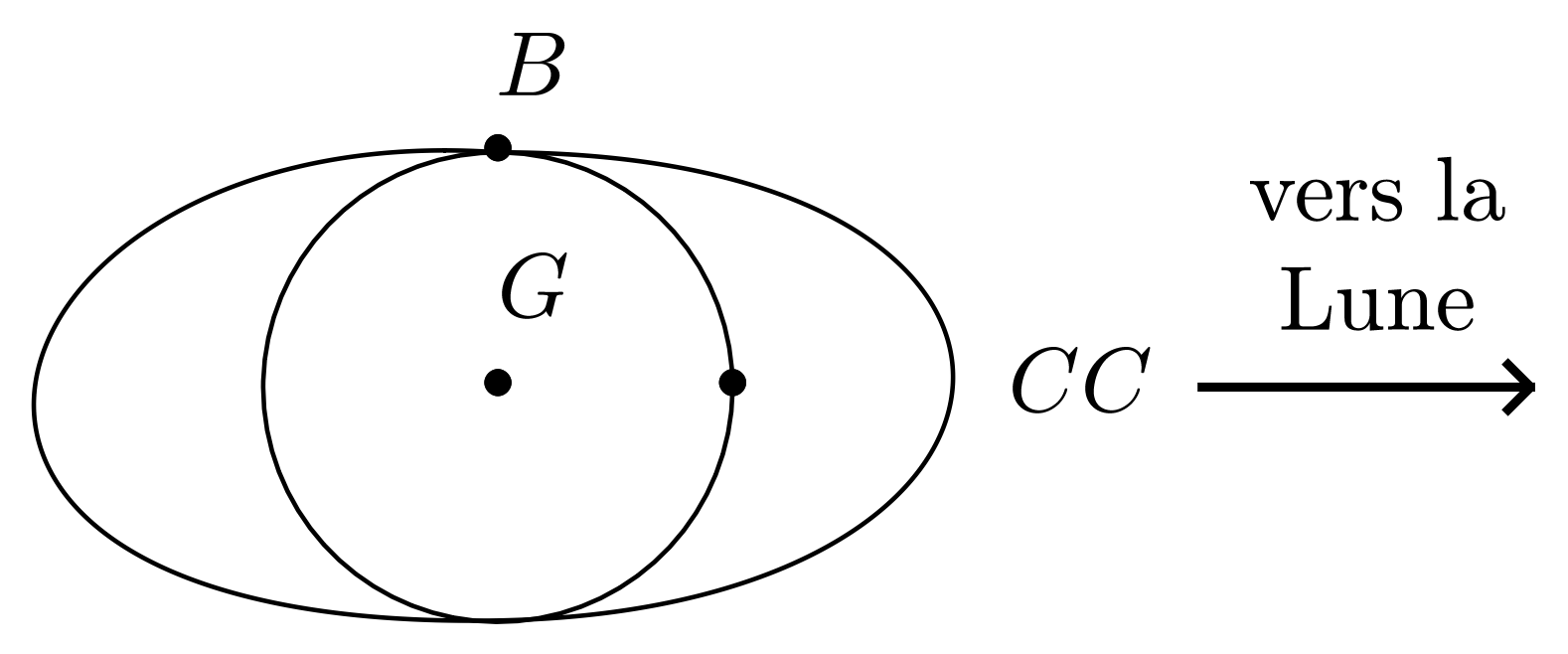
-
$\frac{1}{r + R} = \frac{1}{r} \cdot \frac{1}{1 + \frac{R}{r}} = \frac{1}{r} \left( 1 + \frac{R}{r} \right)^{- 1} \approx \frac{1}{r} \left( 1 - \frac{R}{r} \right)$ puisque $R \ll r$.
De même $\frac{1}{r - R} = \frac{1}{r} \cdot \frac{1}{1 - \frac{R}{r}} = \frac{1}{r} \left( 1 - \frac{R}{r} \right)^{- 1} \approx \frac{1}{r} \left( 1 + \frac{R}{r} \right)$ pour la même raison. ↩︎