Problématique
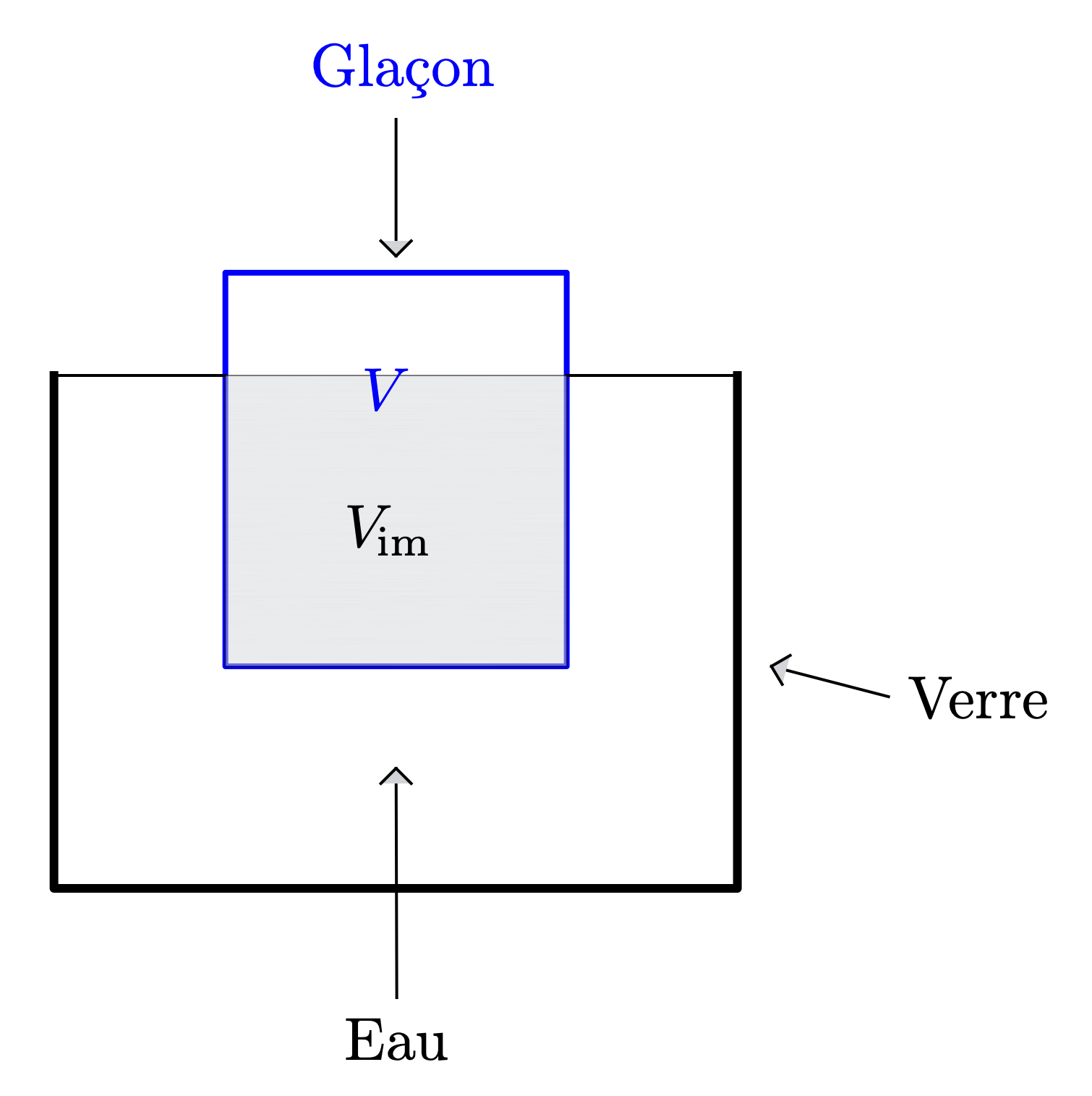
On introduit un glaçon dans un verre d’eau et on ajoute de l’eau liquide de telle sorte que cette dernière affleure.
Que va-t-il se passer à la fonte du glaçon ? L’eau va-t-elle déborder du verre ?
Données
On note
- $V_g$ le volume du glaçon et $V_{im}$ le volume immergé du glaçon ;
- $\rho_l$ la masse volumique de l’eau liquide et $\rho_g$ la masse volumique de l’eau solide ;
- $V_f$ le volume occupé par l’eau initialement sous forme de glace une fois transformée en liquide ;
- On néglige la poussée d’archimède qui s’exerce sur la partie émergée du glaçon ;
- On note $g$ l’accélération du champ de pesanteur.
Résolution du problème
- Lorsque du changement de phase du glaçon $$ \ce{H2O (sol) –> H2O (liq)} $$ y a-t-il conservation de la quantité de matière d’eau (du glaçon) ?
Réponse
Comme la transformation physique est totale, la quantité de matière d’eau dans l’état initial est égale à la quantité d’eau dans l’état final : $n_g(\ce{H2O}) = n_l(\ce{H2O})$.
- Déduire de la question précédante la relation entre la masse volumique de la glace $\rho_g$ et la masse volumique de l’eau $\rho_l$.
Cette relation doit faire intervenir, en plus des deux grandeurs juste citées, $V$ et $V_f$.
Réponse
Puisque $n_g(\ce{H2O}) = n_l(\ce{H2O})$ et comme $M_g(\ce{H2O}) = M_l(\ce{H2O})$, $m_g(\ce{H2O}) = m_l(\ce{H2O})$.
On a donc $$\rho_g\, V = \rho_l\, V_f$$
- En étudiant l’équilibre mécanique du système {glaçon}, déterminer la relation qui existe entre le volume du glaçon et le volume immergé.
Cette relation doit aussi faire intervenir les masses volumiques de l’eau liquide et de la glace.
Réponse
- Système : {glaçon}
- Référentiel : {terrestre considéré galiléen}
- Interactions :
- système – Terre, modélisée par le poids, de valeur $$P = m_g\, g = \rho_g V g$$
- système – Eau, modélisée par la poussée d’archimède, de valeur $$\Pi = m_{\text{fluide déplacé}}\, g = \rho_l V_{im}\, g$$
- Schéma :
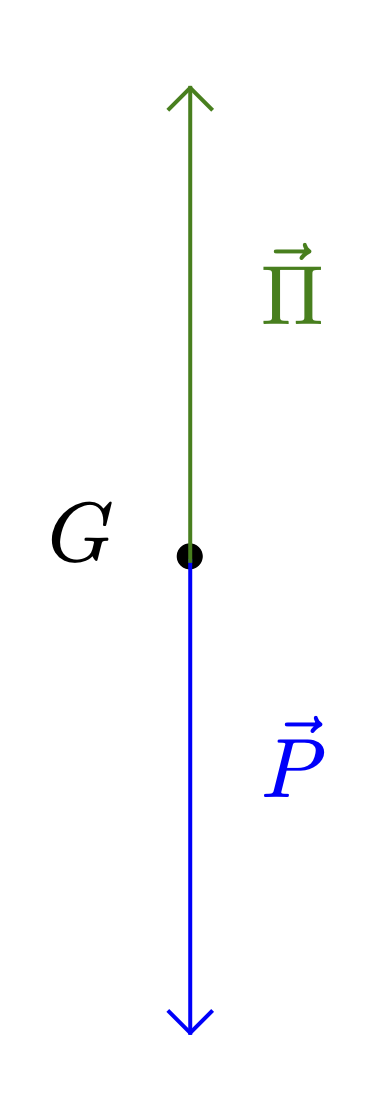
- Deuxième loi de Newton $$ m_g\, \vec{a} = \overrightarrow{P} + \overrightarrow{\Pi} $$ comme le système est immobile, $\vec{a} = \vec{0}$, donc $$ \overrightarrow{P} + \overrightarrow{\Pi} = \vec{0} \iff \overrightarrow{P} = - \overrightarrow{\Pi} $$ $\overrightarrow{P}$ et $\overrightarrow{\Pi}$ sont des vecteurs colinéaires de sens opposés, on a donc $$ P = \Pi \iff \rho_g V g = \rho_l V_{im}\, g $$ Finalement $$ \rho_g V = \rho_l V_{im} $$
- À partir des réponses aux questions 2. et 3., répondre à la problématique.
Réponse
- Réponse à la question 2. : $\rho_g V = \rho_l V_f $ ;
- Réponse à la question 3. : $\rho_g V = \rho_l V_{im}$.
On a donc $$\rho_l V_f = \rho_l V_{im}$$ ou $$ V_f = V_{im}$$ Le volume final occupé par l’eau liquide résultant de la fonte du glaçon est égal au volume immergé du glaçon. Aucun volume supplémentaire, par rapport à la situation initiale, n’est nécessaire, l’eau ne va pas déborder du verre.