
|
Le texte ci-dessous décrit le comportement d'un objet, communément appelé « ludion », plongé dans une colonne d'eau.
« Dans le liquide est une petite figure d'émail, soutenue par une boule de verre creuse qui contient de l'air et de l'eau… Cette boule est percée à sa partie inférieure, d'une petite ouverture par laquelle l'eau peut pénétrer ou sortir, selon que l'air intérieur de la boule est plus ou moins comprimé… Si l'on exerce avec la main une pression sur le piston comme le montre la figure, l'air qui est au-dessous se trouve comprimé et transmet la pression à l'eau du vase et à l'air qui est dans la boule… »
Texte et illustration provenant de : A.GANOT, Traité de Physique, Ed. Ganot 18070

Au laboratoire, le ludion peut être réalisé à
l'aide d'une bille (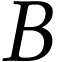 ) de
verre de volume
) de
verre de volume 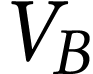 , symbolisant
la figurine solide, placée dans un ballon de baudruche (
, symbolisant
la figurine solide, placée dans un ballon de baudruche (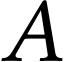 ) fermé et
imperméable, renfermant de l'air de volume variable
) fermé et
imperméable, renfermant de l'air de volume variable 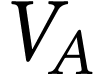 ; le ludion a donc un volume variable
; le ludion a donc un volume variable 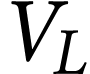 tel que
tel que 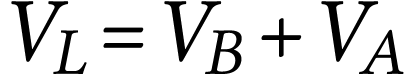 . Il est placé
dans une éprouvette cylindrique verticale (
. Il est placé
dans une éprouvette cylindrique verticale ( ), remplie d'eau sur une hauteur
), remplie d'eau sur une hauteur 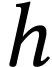 très supérieure aux dimensions du ludion et fermée
dans sa partie supérieure par une membrane souple
imperméable (
très supérieure aux dimensions du ludion et fermée
dans sa partie supérieure par une membrane souple
imperméable (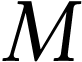 ).
Lorsque l'on n'appuie pas sur la membrane, le ludion est en
équilibre en un point voisin de la surface de l'eau
(figure 1). Lorsque l'on appuie sur la membrane (
).
Lorsque l'on n'appuie pas sur la membrane, le ludion est en
équilibre en un point voisin de la surface de l'eau
(figure 1). Lorsque l'on appuie sur la membrane (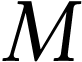 ), on constate que le ludion tombe
au fond de l'éprouvette (figure 2).
), on constate que le ludion tombe
au fond de l'éprouvette (figure 2).
On se propose d'interpréter sommairement cette observation.
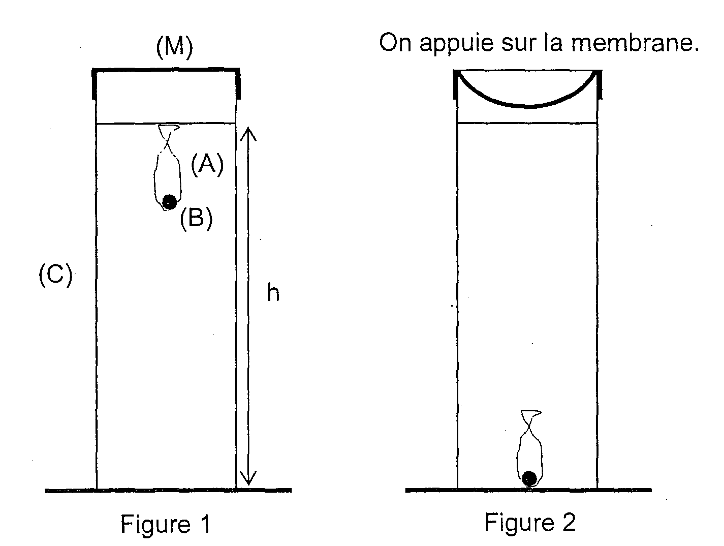
Masse du ludion (bille + ballon + air dans le ballon) : 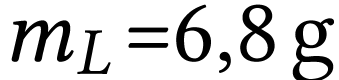 ;
;
Volume de la bille : 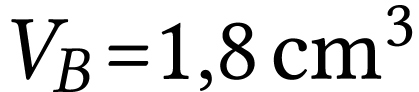 ;
;
Masse volumique de l'eau : 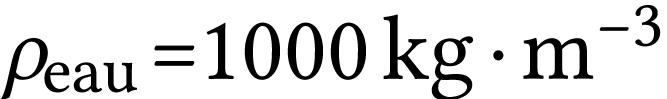 ;
;
Intensité de la pesanteur : 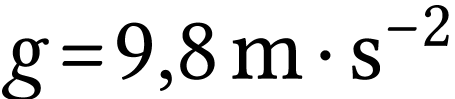 ;
;
Équation d'état des gaz parfaits : 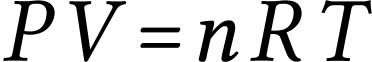 . Dans cette équation
. Dans cette équation 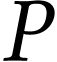 , la pression du gaz, est en Pascal (Pa),
, la pression du gaz, est en Pascal (Pa),
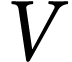 , son volume, en
mètres cubes (
, son volume, en
mètres cubes (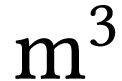 ),
),
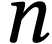 , la quantité de
matière, en moles (mol),
, la quantité de
matière, en moles (mol), 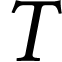 ,
la température, en Kelvin (K).
,
la température, en Kelvin (K). 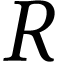 est
la constante des gaz parfaits (
est
la constante des gaz parfaits (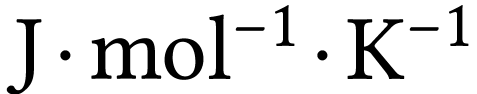 )
;
)
;
La température est constante et égale à 298 K.



Le système interagit avec l'eau. On modélise cette
interaction par le poids 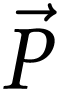 ;
;
Le système interagit avec l'eau. On modélise cette
interaction par la poussée d'Archimède  lorsque le système est immobile. Lorsque le
système est en mouvement, on ajoute une force de
frottement fluide à cette modélisation.
lorsque le système est immobile. Lorsque le
système est en mouvement, on ajoute une force de
frottement fluide à cette modélisation.
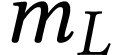 ,
,  ,
,
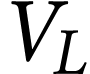 et
et 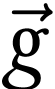 .
.


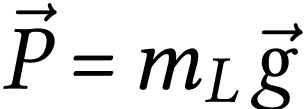 ;
;

Rappel : la poussée d'Archimède est opposée au poids. Sa valeur est celle du poids d'eau déplacé par le système.
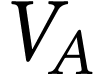 le volume d'air enfermé dans le
ballon lorsque le ludion est en équilibre. Établir son
expression littérale en fonction de
le volume d'air enfermé dans le
ballon lorsque le ludion est en équilibre. Établir son
expression littérale en fonction de 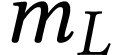 ,
,  et
et 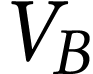 .
.


Puisque le système est immobile, son accélération est nulle. La deuxième loi de Newton s'écrit donc
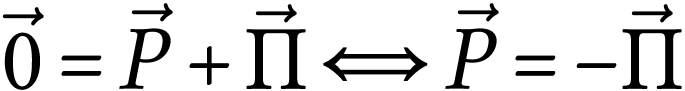
Le poids et la poussée d'Archimède sont donc deux vecteurs colinéaires et de sens opposés. Les valeurs sont donc telles que
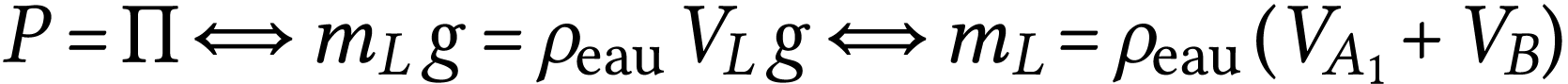
Finalement
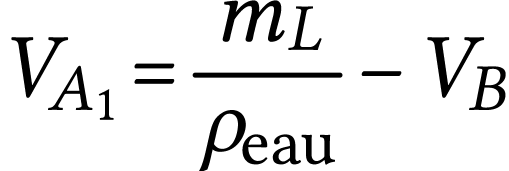
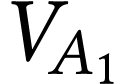 .
.


A.N. 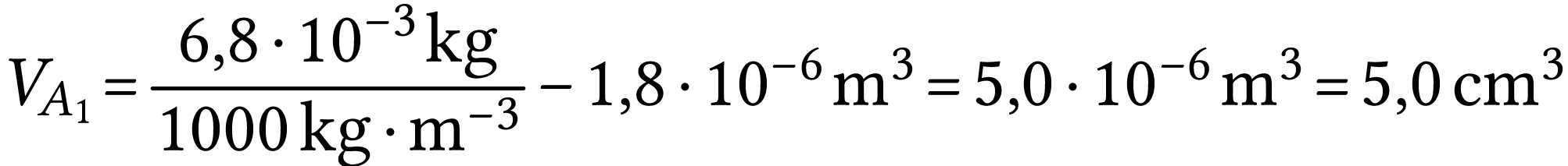 .
.
L'eau est supposée incompressible. La compression de la membrane augmente globalement la pression de l'eau sur l'air enfermé dans le ludion.


L'air dans le ludion est considéré comme un gaz parfait donc :
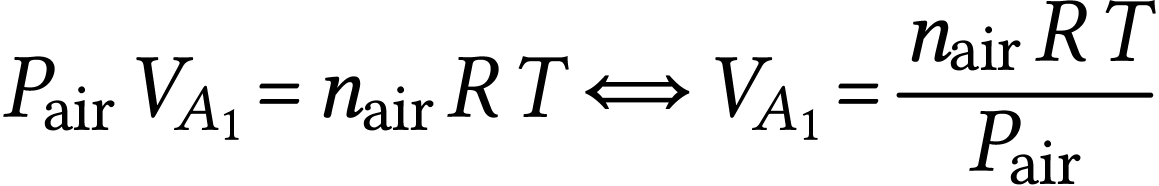
Le volume du ludion diminue donc lorsque la pression qui s'exerce sur lui augmente.


Si le volume 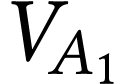 diminue, le volume
diminue, le volume 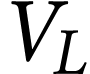 diminue aussi puisque le volume
diminue aussi puisque le volume 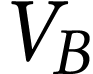 reste constant. La poussée d'Archimède diminue donc
aussi puisqu'elle est proportionnelle au volume
reste constant. La poussée d'Archimède diminue donc
aussi puisqu'elle est proportionnelle au volume 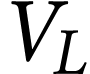 . L'équilibre est rompu et le ludion
se déplace vers le bas.
. L'équilibre est rompu et le ludion
se déplace vers le bas.
Pour étudier le mouvement du ludion, on se place dans le
référentiel du laboratoire. On définit un axe
vertical 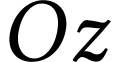 dirigé vers le bas, le point
dirigé vers le bas, le point
 coïncide avec le centre d'inertie du ludion
à l'instant de date
coïncide avec le centre d'inertie du ludion
à l'instant de date 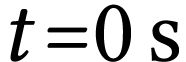 (instant où le
ludion débute sa descente).
(instant où le
ludion débute sa descente).
On suppose que le ludion est soumis à une force de frottement
s'exprimant sous la forme 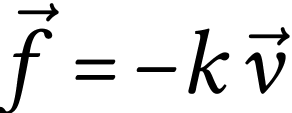 où
où 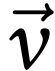 est le vecteur vitesse du centre d'inertie de la bille et
est le vecteur vitesse du centre d'inertie de la bille et
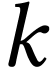 le coefficient de frottement (
le coefficient de frottement (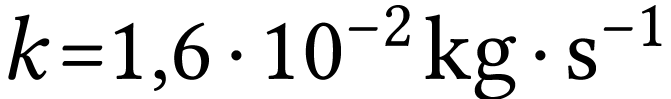 ).
).
On néglige la variation de pression avec la profondeur et on
considère que la pression de l'eau sur l'air enfermé dans
le ludion est la même quelle que soit l'ordonnée 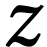 du ludion afin que la valeur de la poussée
d'Archimède puisse être considérée constante.
Le volume d'air du ludion est désormais
du ludion afin que la valeur de la poussée
d'Archimède puisse être considérée constante.
Le volume d'air du ludion est désormais 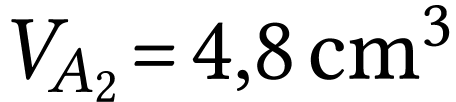 et est supposé constant sur l'ensemble de la descente.
et est supposé constant sur l'ensemble de la descente.


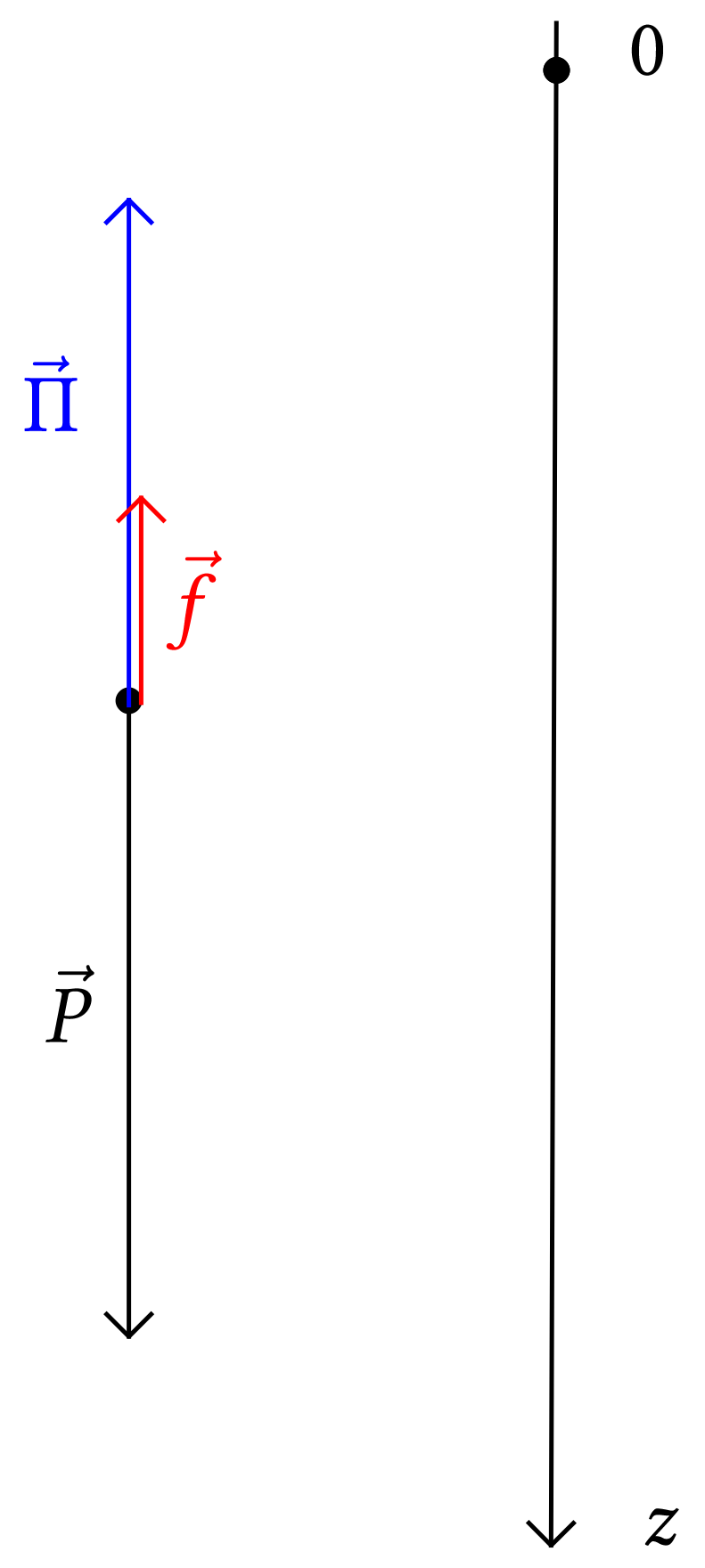


On applique la deuxième loi de Newton
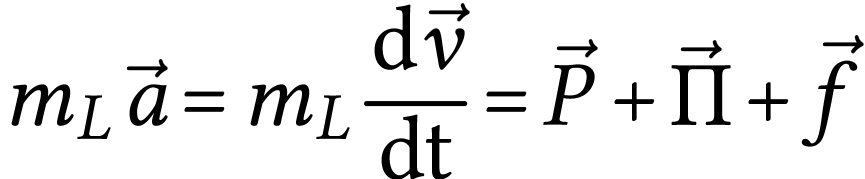
Une projection selon l'axe 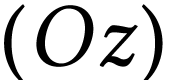 donne
donne
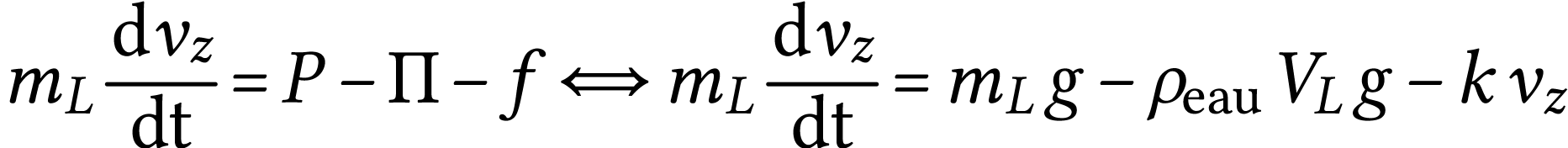
ou
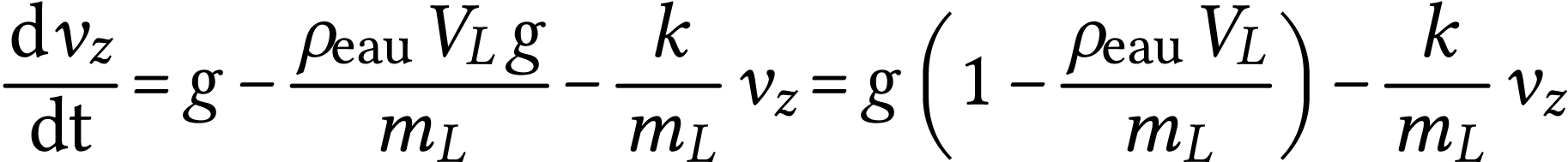
Puisque 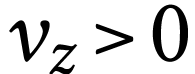 (le ludion descend), on a
(le ludion descend), on a 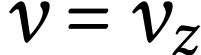 ; l'équation différentielle
s'écrit
; l'équation différentielle
s'écrit
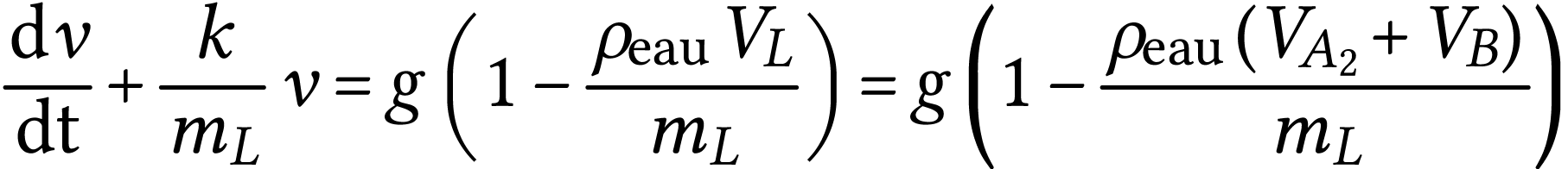
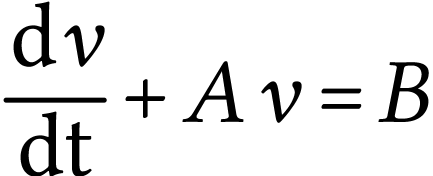 en donnant l'expression de
en donnant l'expression de 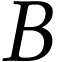 en fonction de
en fonction de 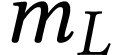 ,
,  ,
, 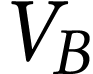 et
et
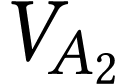 .
.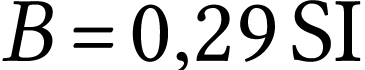 en précisant son
unité.
en précisant son
unité.


Par identification, on conclut que
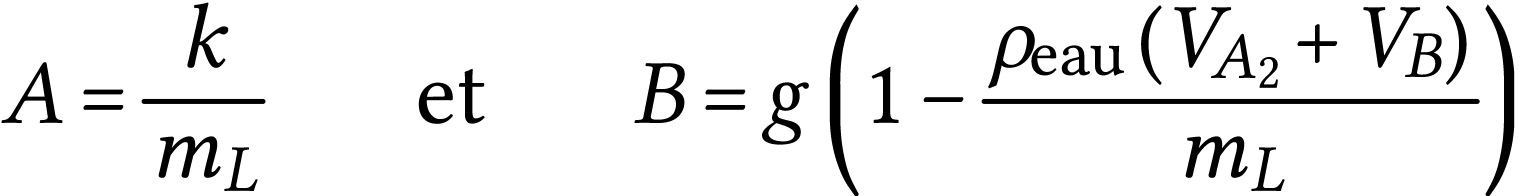
A.N. 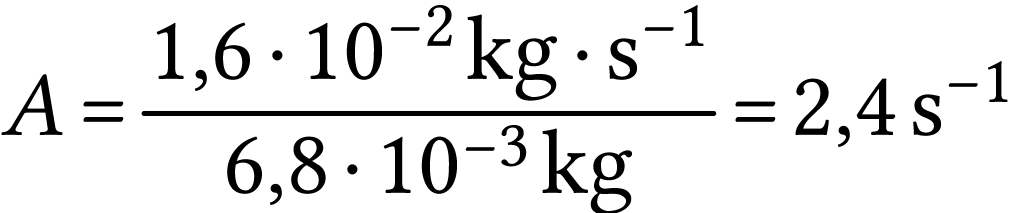 et
et 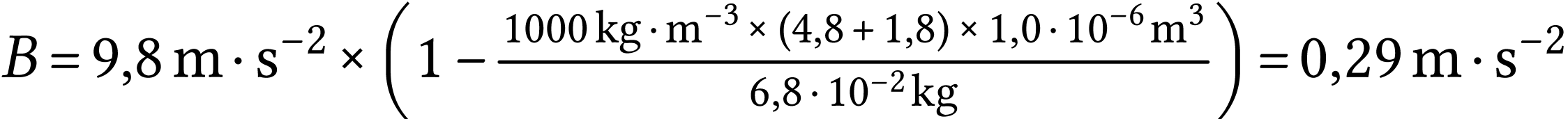 .
.
Partie Hors-Programme
On veut résoudre numériquement cette équation différentielle par la méthode numérique la plus simple : la méthode d'Euler.
À une date t donnée, on suppose que la
dérivée 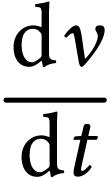 est constante
pendant un cours intervalle de temps
est constante
pendant un cours intervalle de temps 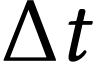 appelé « pas d'intégration ».
appelé « pas d'intégration ».
À partir de l'équation différentielle et des
conditions initiales 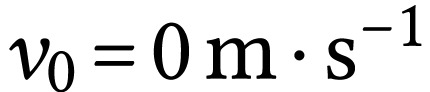 à
à 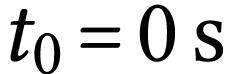 , on calcule la valeur de la
dérivée, puis la valeur de la vitesse
, on calcule la valeur de la
dérivée, puis la valeur de la vitesse 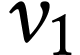 à la date
à la date 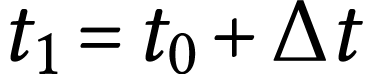 égale à
égale à 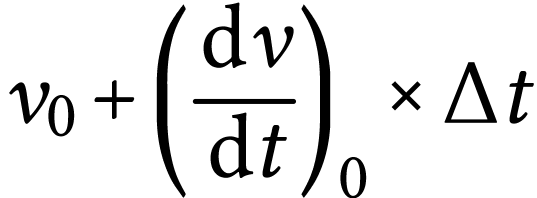 .
C'est une approximation affine !
.
C'est une approximation affine !
On recommence en considérant la date suivante, 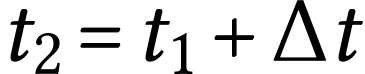 ; la valeur de
; la valeur de 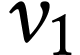 constitue la
nouvelle condition initiale. Et ainsi de suite…
constitue la
nouvelle condition initiale. Et ainsi de suite…

Le tableau suivant est un extrait d'une feuille de calcul des valeurs de
la vitesse (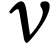 ) et de
l'accélération (
) et de
l'accélération ( )
du ludion en fonction du temps (
)
du ludion en fonction du temps (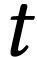 ).
Il correspond aux valeurs
).
Il correspond aux valeurs 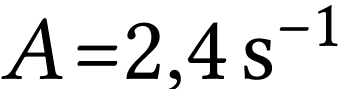 et
et 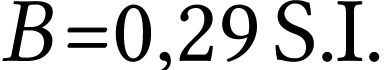
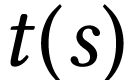 |
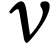 ( (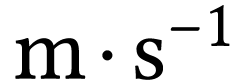 ) ) |
 ( (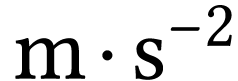 ) ) |
| 0,00 | 0,00 | 0,29 |
| 0,10 | 0,03 | 0,22 |
| 0,20 | 0,05 | 0,17 |
| 0,30 | 0,07 | 0,13 |
| 0,40 | 0,08 | 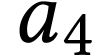 |
| 0,50 | 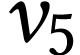 |
0,07 |
| 0,60 | 0,10 | 0,06 |
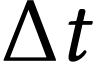 manifestement choisi ?
manifestement choisi ?


Le pas d'itération est 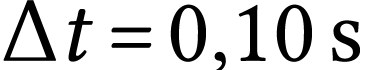 puisqu'on
passe d'une date à la suivante en ajoutant
puisqu'on
passe d'une date à la suivante en ajoutant 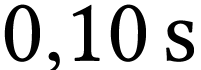 .
.
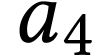 et
et 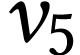 en détaillant les calculs.
en détaillant les calculs.


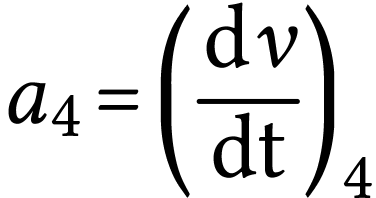 donc
donc 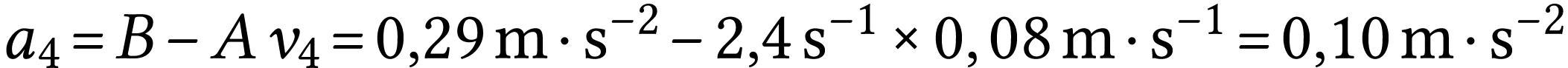 .
.
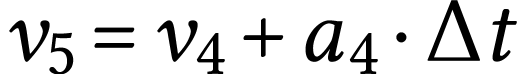 donc
donc 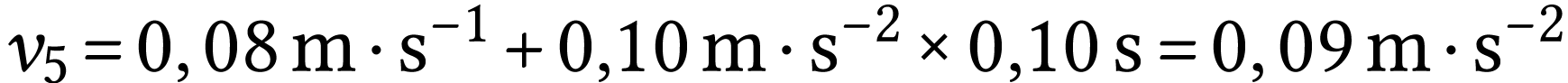 .
.
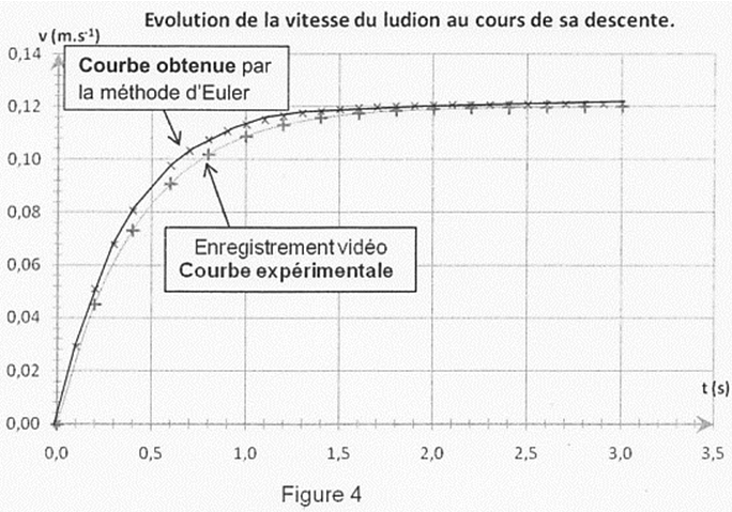
On a représenté sur le même graphique (figure 4) les courbes d'évolution de la vitesse du ludion au cours du temps pendant sa descente obtenues, d'une part par pointage vidéo et traitement informatique, d'autre part par la méthode d'Euler.


En diminuant le pas d'itération dans la méthode d'Euler, on augmente la précision de la méthode ; la courbe de la méthode d'Euler se rapprocherait alors de la courbe expérimentale mais le nombre de lignes de calcul augmenterait.
Attention : si on diminue trop le pas et qu'on augmente le nombre de calcul, on augmente aussi l'erreur due à l'arrondi.
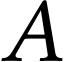 et
et 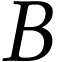 puis sa valeur.
Vérifier qu'elle est en accord avec l'expérience.
puis sa valeur.
Vérifier qu'elle est en accord avec l'expérience.


En régime permanent la vitesse, notée 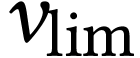 devient constante, donc
devient constante, donc 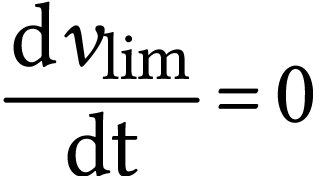 et
et 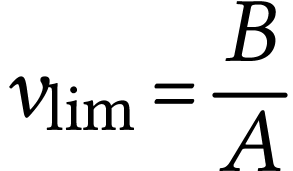 .
.
A.N. 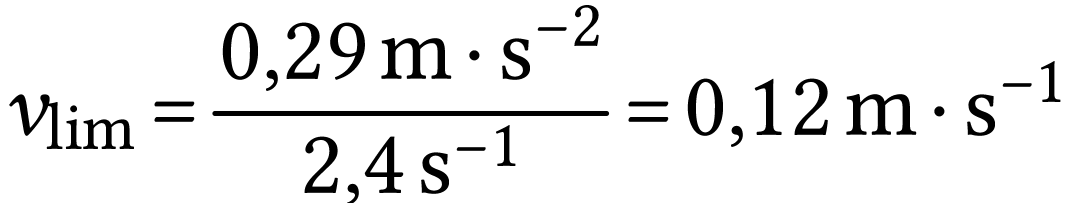 .
Cette valeur est bien en accord avec celle que l'on peut lire sur le
graphe.
.
Cette valeur est bien en accord avec celle que l'on peut lire sur le
graphe.