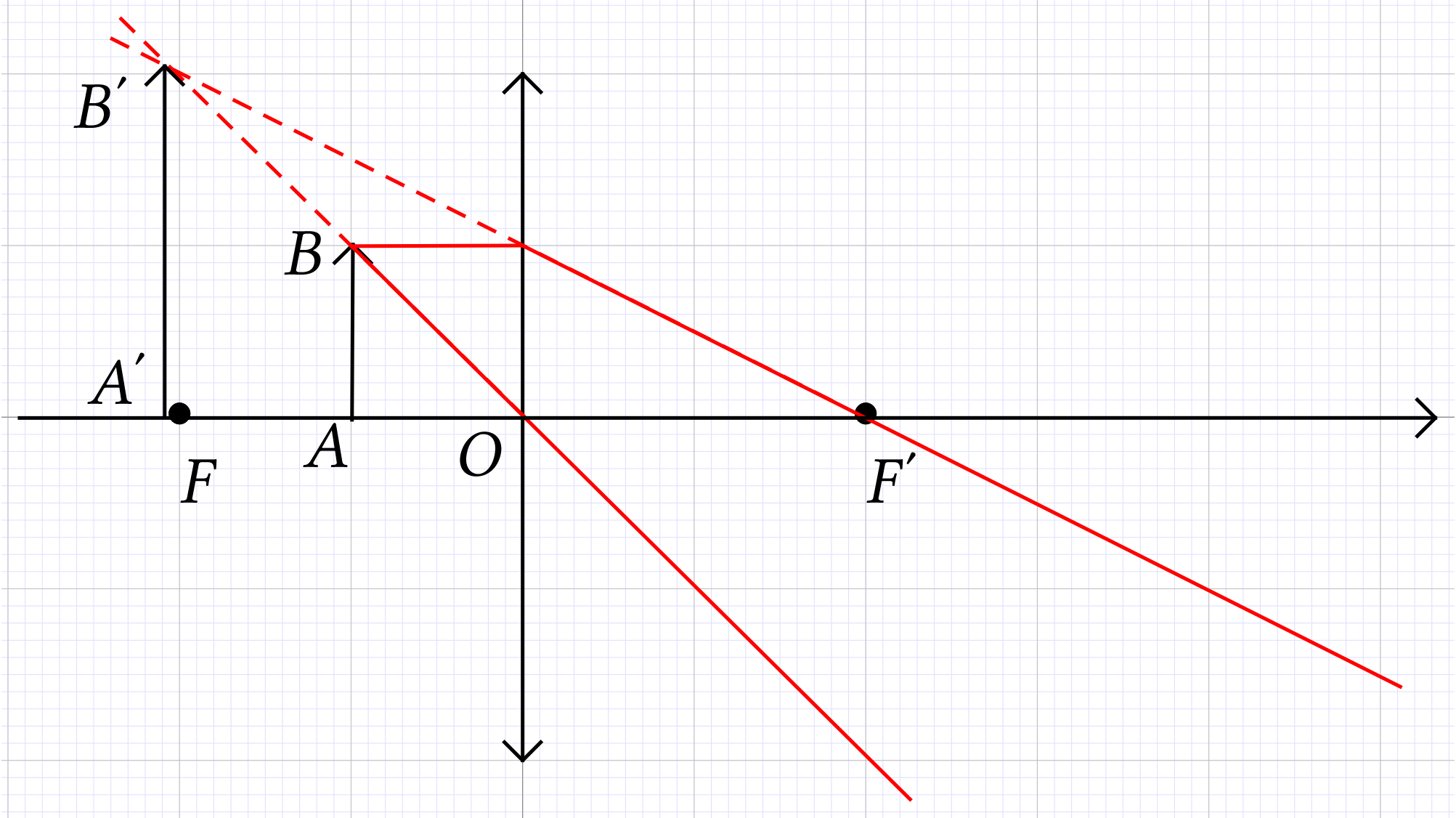
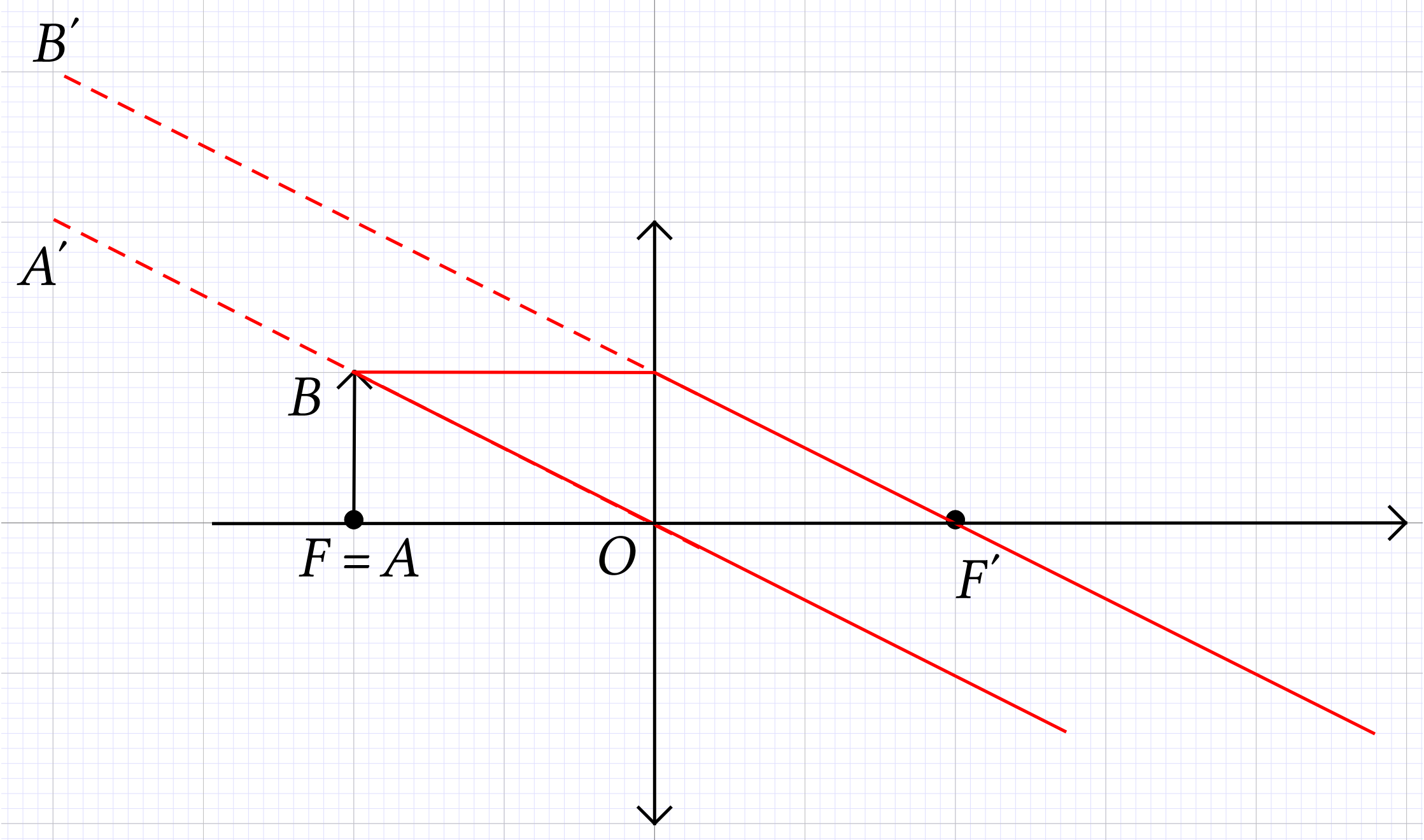
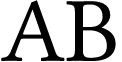 de hauteur 3,5 cm, d'une lentille convergente
de hauteur 3,5 cm, d'une lentille convergente  de
centre
de
centre 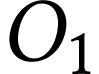 , de distance focale
, de distance focale
 , d'une lentille
, d'une lentille  de centre
de centre 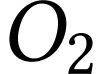 , de
distance focale
, de
distance focale 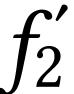 inconnue et d'un écran.
Le point objet
inconnue et d'un écran.
Le point objet  est situé sur l'axe
optique.
est situé sur l'axe
optique.
|
On dispose d'un banc d'optique, d'un objet lumineux 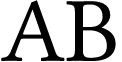 de hauteur 3,5 cm, d'une lentille convergente
de hauteur 3,5 cm, d'une lentille convergente  de
centre
de
centre 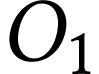 , de distance focale
, de distance focale
 , d'une lentille
, d'une lentille  de centre
de centre 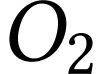 , de
distance focale
, de
distance focale 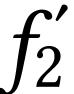 inconnue et d'un écran.
Le point objet
inconnue et d'un écran.
Le point objet  est situé sur l'axe
optique.
est situé sur l'axe
optique.
 . Où
doit-on placer l'écran afin de visualiser une image nette de
. Où
doit-on placer l'écran afin de visualiser une image nette de
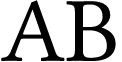 à travers la lentille
à travers la lentille  ?
?


La relation de conjugaison de Descartes permet de déterminer
la position de l'image 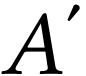 de
de  par la lentille :
par la lentille :
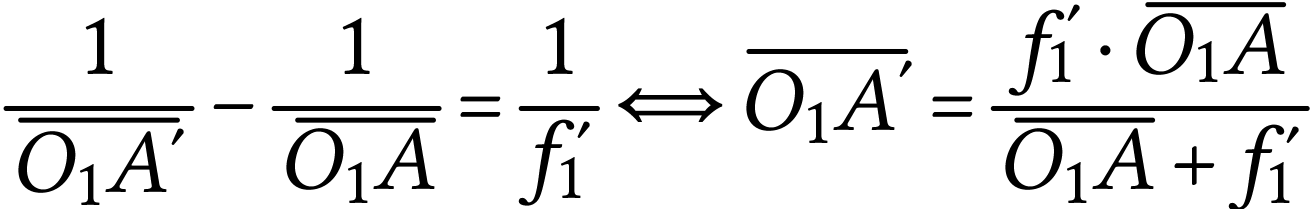
A.N. 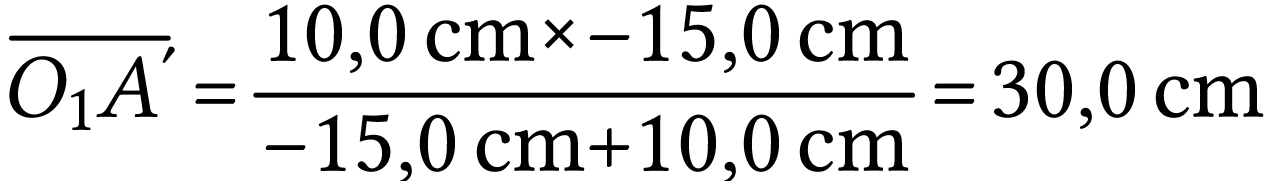 .
.
L'écran doit être placé 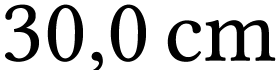 derrière la lentille
derrière la lentille  .
.
 ?
?


Le grandissement est défini par :

Si la lentille est mince et convergente, on montre que
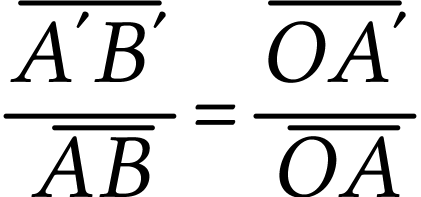
donc



L'image est renversée car le grandissement est négatif.
L'image est plus grande que l'objet car  .
.


Si on utilise la définition du grandissement on obtient

A.N. 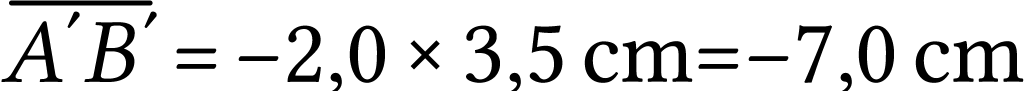 .
.
L'image a pour dimension 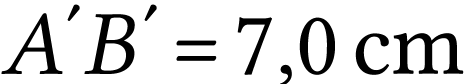 .
.
 par une lentille
convergente
par une lentille
convergente  de vergence
de vergence 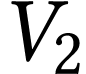 inconnue. Sur le banc d'optique, l'objet est placé à
40,0 cm de la lentille. On visualise une image nette lorsque
l'écran se situe 66,7 cm derrière la lentille.
inconnue. Sur le banc d'optique, l'objet est placé à
40,0 cm de la lentille. On visualise une image nette lorsque
l'écran se situe 66,7 cm derrière la lentille.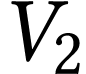 de la
lentille.
de la
lentille.


La relation de conjugaison permet d'écrire
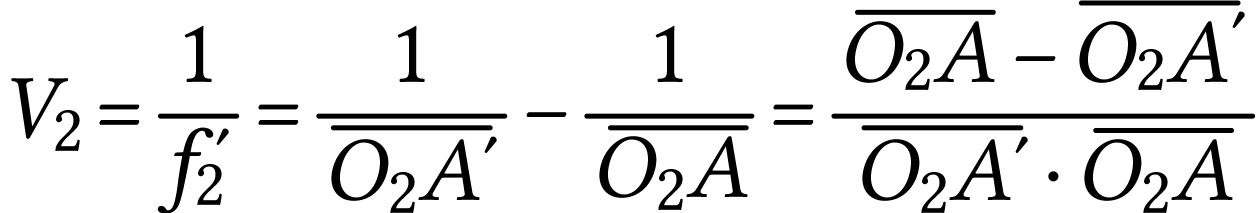
A.N. 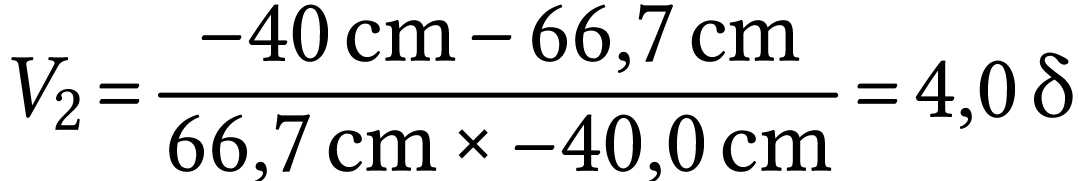 .
.
L'image  d'un objet
d'un objet  donnée par une lentille est renversée et deux fois plus
grande que l'objet. Les points
donnée par une lentille est renversée et deux fois plus
grande que l'objet. Les points  et
et  sont sur l'axe optique de la lentille, ils sont distants
de
sont sur l'axe optique de la lentille, ils sont distants
de  .
.



 et son centre optique
et son centre optique  .
.


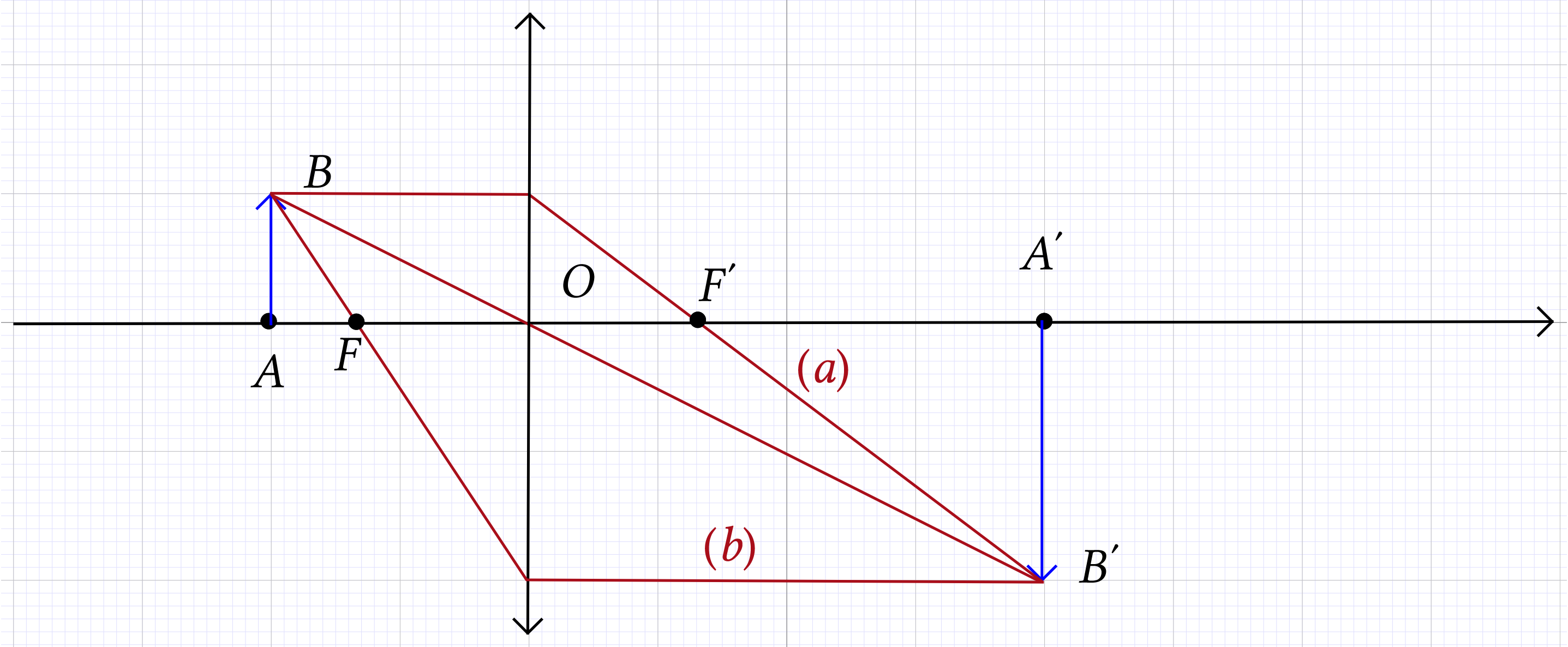
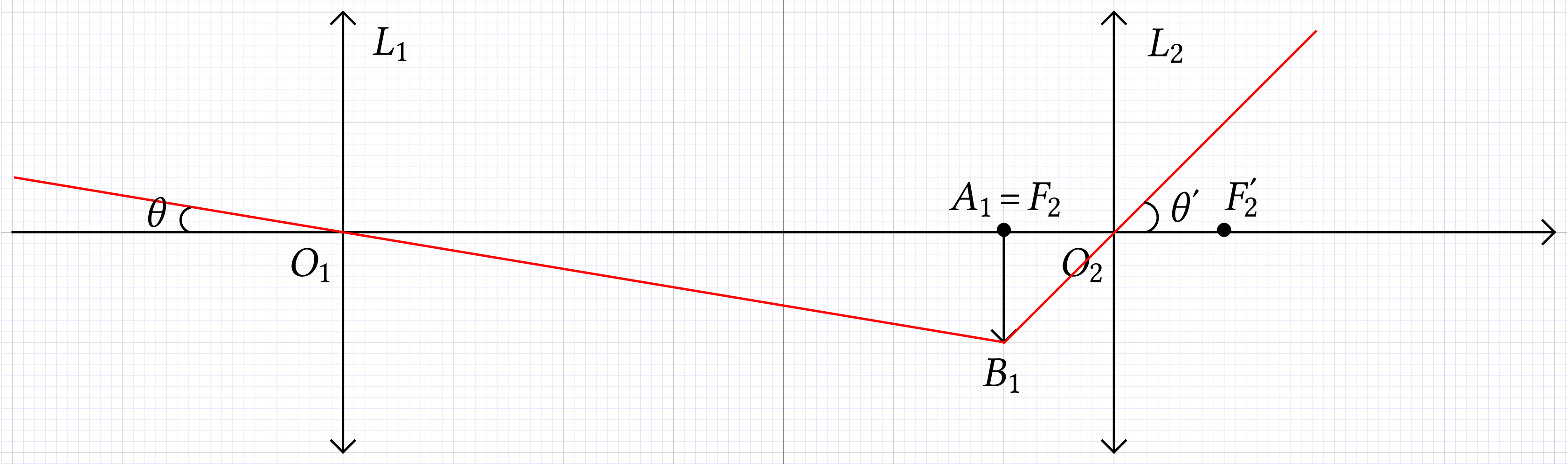
Pour placer la lentille, il faut se rappeler que le rayon issu de
 et qui passe par le centre optique
et qui passe par le centre optique  de la lentille n'est pas dévié.
de la lentille n'est pas dévié.
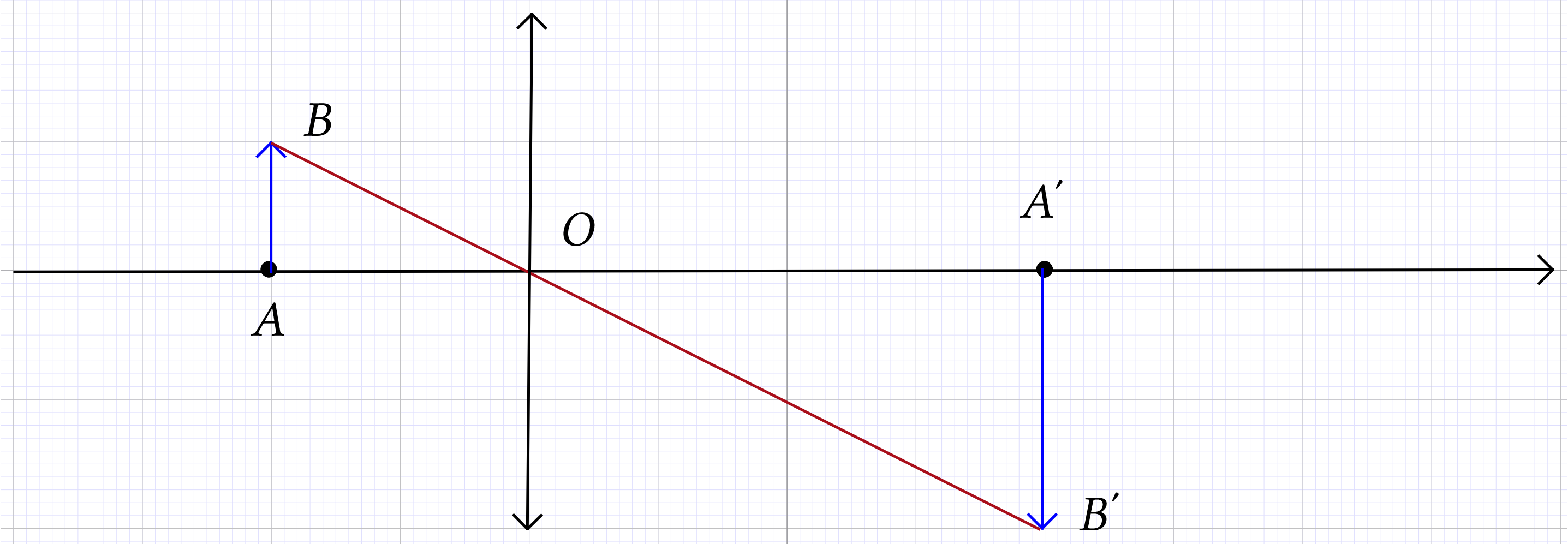
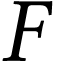 et en déduire la
position du foyer image
et en déduire la
position du foyer image  de cette lentille.
de cette lentille.
Réponse


Le rayon issu de 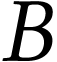 parallèle
à l'axe optique est dévié par la lentille
de telle sorte qu'il passe par le point de l'axe optique
appelé foyer image
parallèle
à l'axe optique est dévié par la lentille
de telle sorte qu'il passe par le point de l'axe optique
appelé foyer image  de la
lentille (rayon
de la
lentille (rayon  sur la figure).
sur la figure).
Le rayon issu de 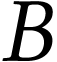 qui ressort de la
lentille parallèle à l'axe optique est
passé, en amont de la lentille par un point appelé
foyer objet
qui ressort de la
lentille parallèle à l'axe optique est
passé, en amont de la lentille par un point appelé
foyer objet 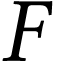 de la lentille
(rayon
de la lentille
(rayon  sur la figure).
sur la figure).
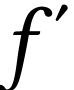 de la lentille ?
de la lentille ?


On détermine graphiquement que 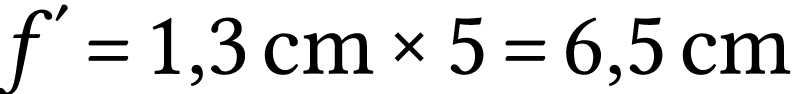
 dans les conditions d'utilisation.
dans les conditions d'utilisation.


Le grandissement vaut 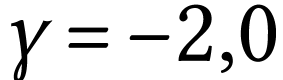 puisque l'image est
deux fois plus grande que l'objet et qu'elle est renversée.
puisque l'image est
deux fois plus grande que l'objet et qu'elle est renversée.
 et
et 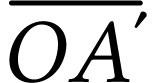 .
.


On a montré dans le cours que, dans le cadre du modèle des lentilles minces convergentes,
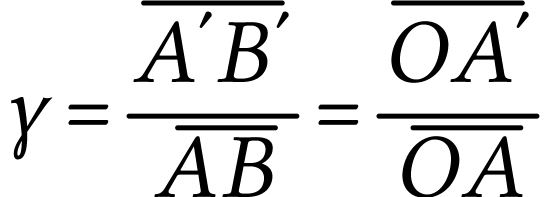
On détermine graphiquement que  et
et
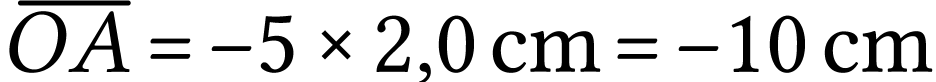 . On retrouve donc bien
un grandissement
. On retrouve donc bien
un grandissement 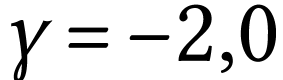 .
.
Pour réaliser une loupe on utilise une lentille mince convergente. La finalité d'une loupe est d'obtenir d'un objet une image plus grande et droite.


Si l'image est plus grande et droite, 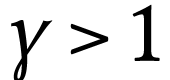 donc
il est positif et sa valeur absolue est supérieure à
1.
donc
il est positif et sa valeur absolue est supérieure à
1.
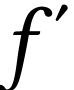 lorsque :
lorsque :
l'objet se situe à une distance comprise entre 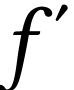 et
et  ;
;
l'objet se situe à une distance comprise entre le centre
optique  de la lentille et son foyer objet
de la lentille et son foyer objet
 .
.



Lorsque l'objet est situé en amont de la lentille à
une distance comprise entre  et
et  , l'image est renversée, plus grande
que l'objet et située au-delà de
, l'image est renversée, plus grande
que l'objet et située au-delà de  après la lentille. Elle est réelle.
après la lentille. Elle est réelle.
Lorsque l'objet est situé en amont de la lentille entre  et
et  ,
l'image est droite, plus grande que l'objet et située en
amont de la lentille. Elle est virtuelle.
,
l'image est droite, plus grande que l'objet et située en
amont de la lentille. Elle est virtuelle.


Pour pouvoir être utilisée en loupe, la lentille doit
être placée de telle sorte que l'objet soit compris
entre  et
et  .
.
 de distance focale
de distance focale  . On désire obtenir un grandissement
égal à
. On désire obtenir un grandissement
égal à  .
Calculer les positions de l'objet et de l'image par rapport à
la lentille.
.
Calculer les positions de l'objet et de l'image par rapport à
la lentille.


On doit résoudre le système suivant :

Par substitution, on a, puisque 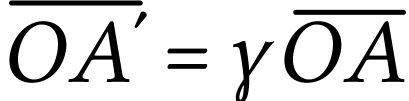 ,
,

soit
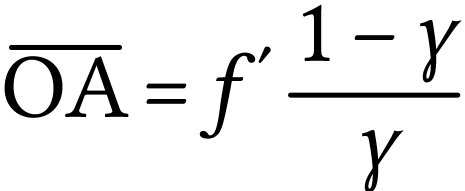
A.N. 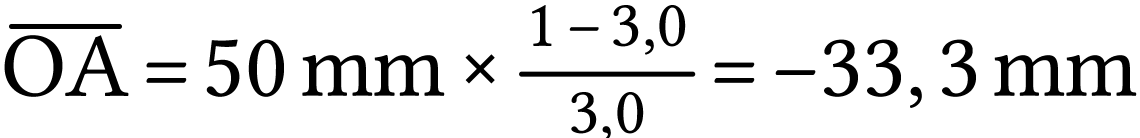 et
et 
La lentille  est toujours utilisée en
loupe. Un œil ne se fatigue pas lorsqu'il observe à
l'infini.
est toujours utilisée en
loupe. Un œil ne se fatigue pas lorsqu'il observe à
l'infini.
 pour que son
image soit rejetée à l'infini ?
pour que son
image soit rejetée à l'infini ?


Pour que l'image soit rejetée à l'infini, l'objet doit être placé dans le plan focal objet de la lentille.


Sur certaines montres indiquant le jour du mois, on place devant ce nombre une lentille convergente afin de le grandir.


Cette lentille fonctionne en loupe ; elle forme une image droite, agradie, virtuelle qui grossit l'objet (ici un nombre).
 de la lentille, l'observation de ce
nombre à travers la lentille doit se faire sans effort pour
l'œil.
de la lentille, l'observation de ce
nombre à travers la lentille doit se faire sans effort pour
l'œil.


Puisque l'observation ne réclame aucun effort à
l'œil, on peut conclure que l'image donnée par la
lentille se situe à l'infini et que l'objet, le nombre, est
dans le plan focal objet. Finalement, 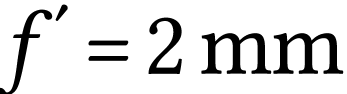 .
.
Format : 16/9
Résolution : W-XGA 1280x768
Taille image : 0,75 m - 7,5 m
Luminosité : 110 ANSI Lumens
Niveau sonore : 25 dB (mode silencieux)/30 dB (mode normal)
Distance : 0,9 m à 10 m
Contraste: > 2500:1
Optique : Lentille de projection : 22 à 27 mm
Lampe : Durée de vie 4 000 heures
Le schéma ci-après représente de façon
très simplifiée le principe d'un vidéo-projecteur.
Une lampe éclaire une lentille convergente  , jouant le rôle de condenseur, placée
devant une plaque de cristaux liquides.
, jouant le rôle de condenseur, placée
devant une plaque de cristaux liquides.

L'image formée sur la plaque représente l'objet pour la
lentille de projection  convergente. On visualise
son image sur un écran.
convergente. On visualise
son image sur un écran.
 , indiquer
comment doit se situer
, indiquer
comment doit se situer  par rapport à la
lentille
par rapport à la
lentille  .
.


On constate que les rayons issus de  quittent
la lentille
quittent
la lentille  parallèlement à
l'axe optique. On peut donc en conclure que
parallèlement à
l'axe optique. On peut donc en conclure que 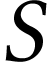 se trouve au foyer objet de la lentille
se trouve au foyer objet de la lentille  .
.
Lorsqu'on utilise une lentille de projection de distance focale 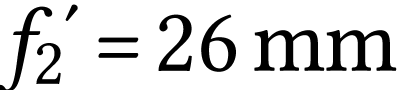 , la diagonale d'une image 16/9 a
pour valeur
, la diagonale d'une image 16/9 a
pour valeur  pour une distance
lentille-écran de
pour une distance
lentille-écran de 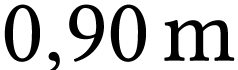 .
.
 ?
?


On nous indique que 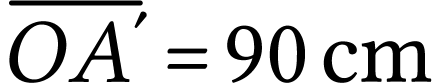 . On
peut donc déterminer la distance entre l'objet et la lentille
à partir de la relation de conjugaison
. On
peut donc déterminer la distance entre l'objet et la lentille
à partir de la relation de conjugaison

A.N. 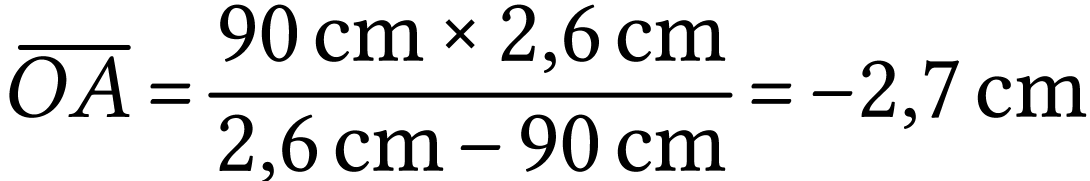 .
.
 et pour hauteur
et pour hauteur 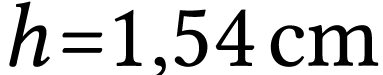 .
.


La définition du grandissement est

Dans le cadre des lentilles minces convergentes, on a montré qu'on peut aussi exprimer le grandissement sous la forme
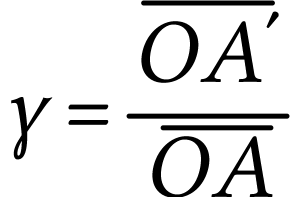
A.N. 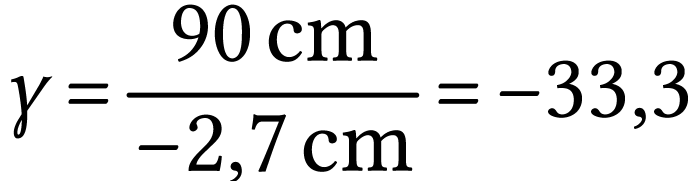 .
L'image est donc 33,3 fois plus grande que l'objet (et
renversée).
.
L'image est donc 33,3 fois plus grande que l'objet (et
renversée).
 A.N.
A.N.
 ;
;
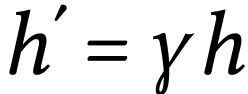 A.N.
A.N.
 .
.


Si on note 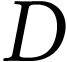 la diagonale,
la diagonale, 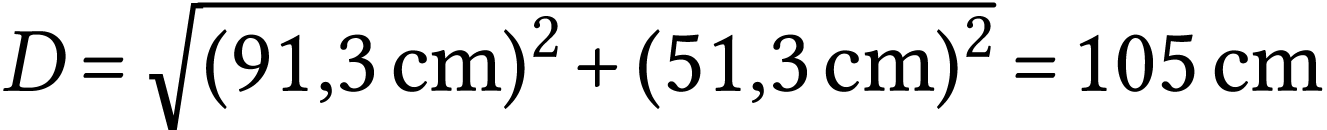 . Cette valeur est très proche de
celle annoncée.
. Cette valeur est très proche de
celle annoncée.


16/9 signifie que le rapport de la largeur de l'image sur sa hauteur est égal à 1,78.
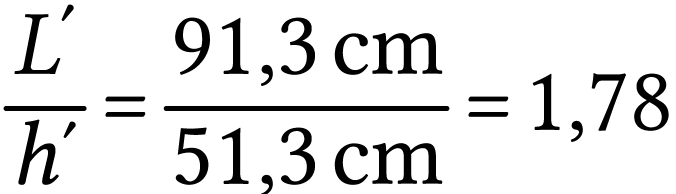 , l'image est bien au
format 16/9.
, l'image est bien au
format 16/9.
Lorsqu'on a peu de recul entre le vidéo-projecteur et
l'écran, on conseille l'utilisation d'un appareil à focale
courte. On sous-entend par focale courte, une distance focale 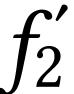 de la lentille de projection petite.
de la lentille de projection petite.
Le
vidéo-projecteur décrit ci-dessus a une lentille  dont la focale
dont la focale 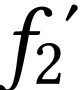 peut varier de
peut varier de  à
à 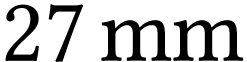 (voir les
caractéristiques).
(voir les
caractéristiques).
 , calculer les
dimensions de la nouvelle image, l'image formée sur la plaque
de cristaux liquides gardant les mêmes dimensions.
, calculer les
dimensions de la nouvelle image, l'image formée sur la plaque
de cristaux liquides gardant les mêmes dimensions.


On conserve les mêmes dimensions ; en particulier, la distance
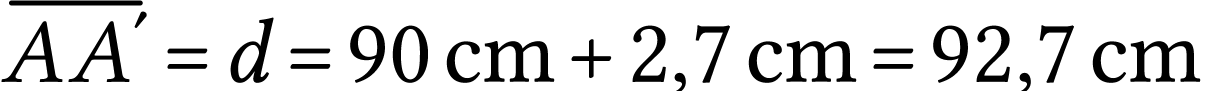 . On doit donc
résoudre le système
. On doit donc
résoudre le système
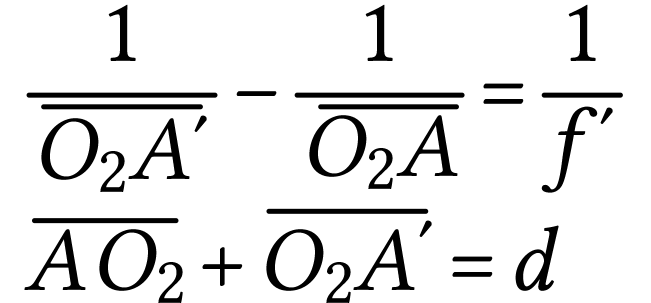
donc  et
et 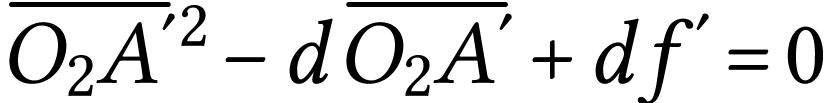 .
.
A.N. 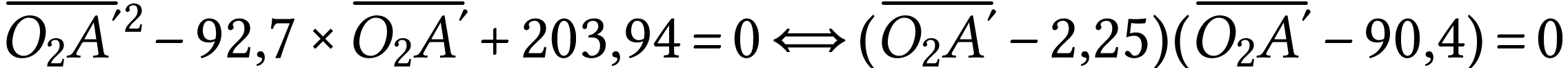 .
La racine qui a un sens physique est
.
La racine qui a un sens physique est 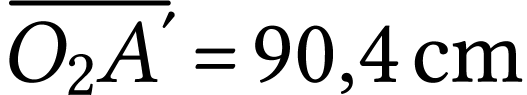 .
On en déduit que
.
On en déduit que  et
et  .
.
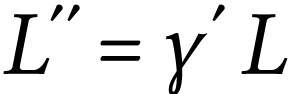 A.N.
A.N.
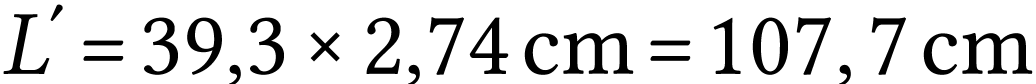 ;
;
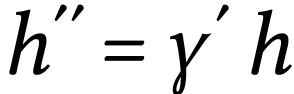 A.N.
A.N.
 .
.


Le conseil est justifié puisque l'image est bien plus grande.
Un appareil photographique comporte deux éléments essentiels : l'objectif et la pellicule.
On modélise :
l'objectif par une lentille mince convergente  de centre optique
de centre optique  ;
;
on note 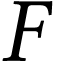 et
et  les
foyers principaux, respectivement objet et image, de cette lentille,
dont la distance focale est :
les
foyers principaux, respectivement objet et image, de cette lentille,
dont la distance focale est :
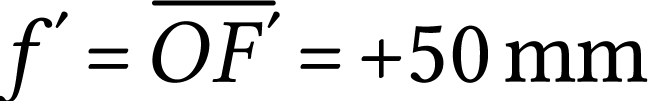
la pellicule par un écran 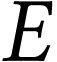 ,
où se forme l'image réelle de l'objet
photographié.
,
où se forme l'image réelle de l'objet
photographié.
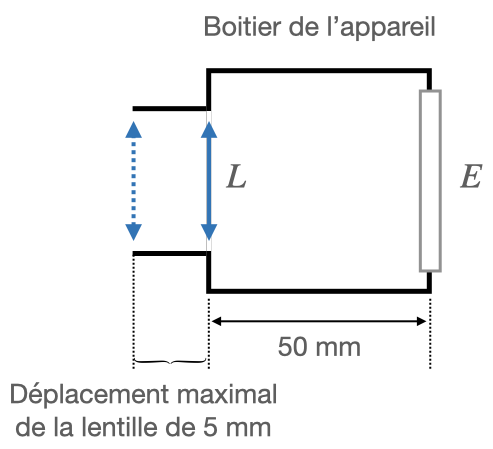
L'objectif est conçu pour pouvoir déplacer la lentille
 par rapport à la pellicule.
par rapport à la pellicule.
 situé à
une très grande distance de
situé à
une très grande distance de  .
En le considérant « à l'infini », et pour
avoir une image nette, à quelle distance
.
En le considérant « à l'infini », et pour
avoir une image nette, à quelle distance  de l'écran
de l'écran  se trouve la lentille
se trouve la lentille  ?
?


Si l'objet est à l'infini, l'image se forme dans le plan
focal image de l'objectif. On a donc 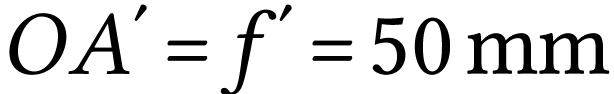 .
.
Pour obtenir des images, sur l'écran  , d'objets plus rapprochés de
, d'objets plus rapprochés de  , il est nécessaire d'effectuer une mise
au point, c'est-à-dire de faire varier la distance
lentille-écran.
, il est nécessaire d'effectuer une mise
au point, c'est-à-dire de faire varier la distance
lentille-écran.
 à photographier se rapproche
de
à photographier se rapproche
de  , la distance entre la
lentille et l'écran doit-elle augmenter ou diminuer ? Justifier
à l'aide d'un schéma.
, la distance entre la
lentille et l'écran doit-elle augmenter ou diminuer ? Justifier
à l'aide d'un schéma.



Si l'objet 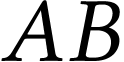 se rapproche du foyer objet de la
lentille, l'image
se rapproche du foyer objet de la
lentille, l'image 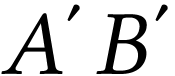 s'éloigne de cette
lentille.
s'éloigne de cette
lentille.
Le déplacement de l'objectif permet d'augmenter de  au maximum la distance entre la lentille et la pellicule
par rapport à sa position quand l'objet est « à
l'infini ».
au maximum la distance entre la lentille et la pellicule
par rapport à sa position quand l'objet est « à
l'infini ».


Si on note  la distance maximale centre
optique de la lentille - écran, on a
la distance maximale centre
optique de la lentille - écran, on a 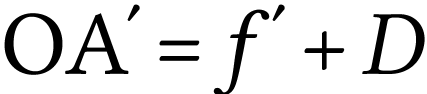 . La relation de conjugaison donne alors
. La relation de conjugaison donne alors
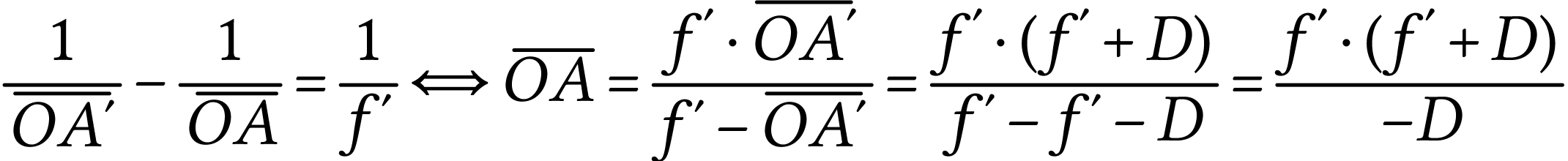
A.N. 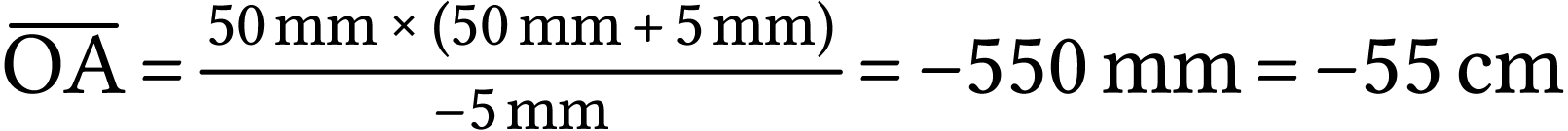 .
On peut donc prendre en photo des objets situés entre
.
On peut donc prendre en photo des objets situés entre  et
et  .
.
 dans ces conditions.
dans ces conditions.


Par définition,

Dans le cas des lentilles minces convergentes, on peut montrer que cette définition entraîne
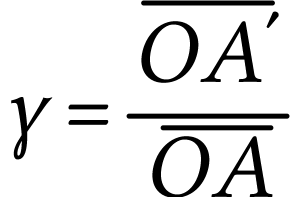
A.N.  .
L'image est donc bien réelle, renversée et 10 fois
plus petite que l'objet.
.
L'image est donc bien réelle, renversée et 10 fois
plus petite que l'objet.
On veut photographier une carte postale de format  .
.
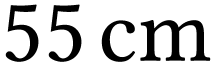 de
de  dans un plan perpendiculaire à l'axe optique de
la lentille
dans un plan perpendiculaire à l'axe optique de
la lentille  , le
grandissement vaut 0,1 en valeur absolue. Quelles seraient les
dimensions de son image sur la pellicule de format
, le
grandissement vaut 0,1 en valeur absolue. Quelles seraient les
dimensions de son image sur la pellicule de format  ?
?


Les dimensions de la carte postale seraient de  .
.
On veut que les dimensions de l'image de la carte postale soient  .
.
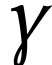 souhaité.
souhaité.


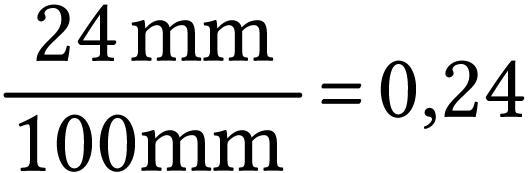 et
et  .
Il faut donc multiplier par 0,24 les dimensions de la carte postale
pour obtenir celles de l'image. Le grandissement attendu vaut donc
.
Il faut donc multiplier par 0,24 les dimensions de la carte postale
pour obtenir celles de l'image. Le grandissement attendu vaut donc
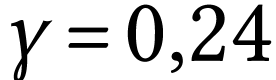 .
.
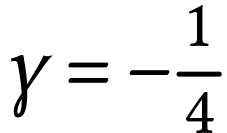 . Calculer alors la distance
. Calculer alors la distance 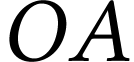 à laquelle on doit placer la carte postale, ainsi que la
distance
à laquelle on doit placer la carte postale, ainsi que la
distance  entre la lentille et l'écran.
entre la lentille et l'écran.


Le problème admet deux inconnues :  et
et
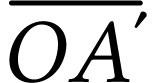 . Il faut donc
résoudre le système
. Il faut donc
résoudre le système

Par substitution, on obtient

et
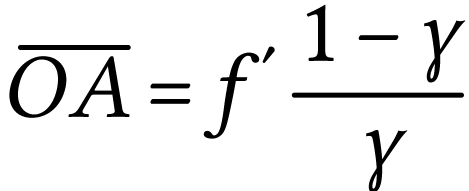
A.N.  et
et 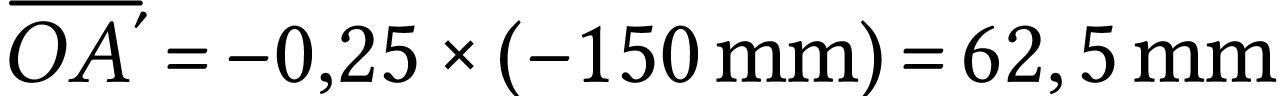 . Il n'est manifestement pas possible
d'obtenir ce grandissement pour la carte postale envisagée
puisque la distance lentille-écran nécessaire est
supérieure à celle que l'on peut régler.
. Il n'est manifestement pas possible
d'obtenir ce grandissement pour la carte postale envisagée
puisque la distance lentille-écran nécessaire est
supérieure à celle que l'on peut régler.
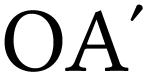 nécessaire trouvée à la question
précédente avec le seul objectif de l'appareil
photographique. Il est toutefois possible d'adapter, entre l'objectif
et le boîtier de l'appareil photographique, un ou plusieurs
tubes creux appelés « bagues allonges » de longueur
nécessaire trouvée à la question
précédente avec le seul objectif de l'appareil
photographique. Il est toutefois possible d'adapter, entre l'objectif
et le boîtier de l'appareil photographique, un ou plusieurs
tubes creux appelés « bagues allonges » de longueur
 . Disposant de bagues
allonges de longueurs
. Disposant de bagues
allonges de longueurs  , 10
mm et
, 10
mm et 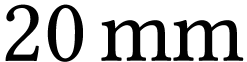 , indiquer :
, indiquer :
laquelle ou lesquelles choisir ;
comment procéder pour que l'image de la carte postale soit
nette sur la pellicule avec pour grandissement 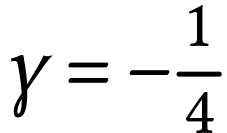 .
.



La bague de 5 mm permet de former des images à une
distance 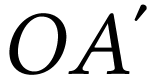 telle que
telle que  . Elle est donc trop courte.
. Elle est donc trop courte.
La bague de 10 mm permet de former des images à une
distance 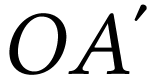 telle que
telle que 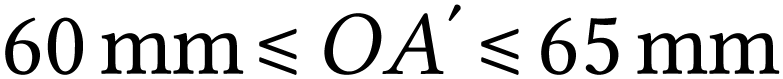 . Elle convient donc.
. Elle convient donc.
La bague de 20 mm permet de former des images à une
distance 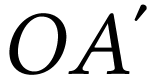 telle que
telle que 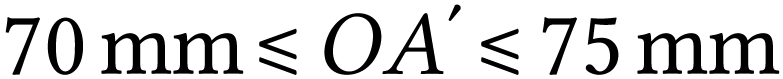 . Elle est donc trop longue.
. Elle est donc trop longue.
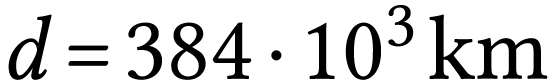 .
Le diamètre de la Lune est environ
.
Le diamètre de la Lune est environ  . Quel est le diamètre apparent de la Lune
pour un observateur terrestre ?
. Quel est le diamètre apparent de la Lune
pour un observateur terrestre ?


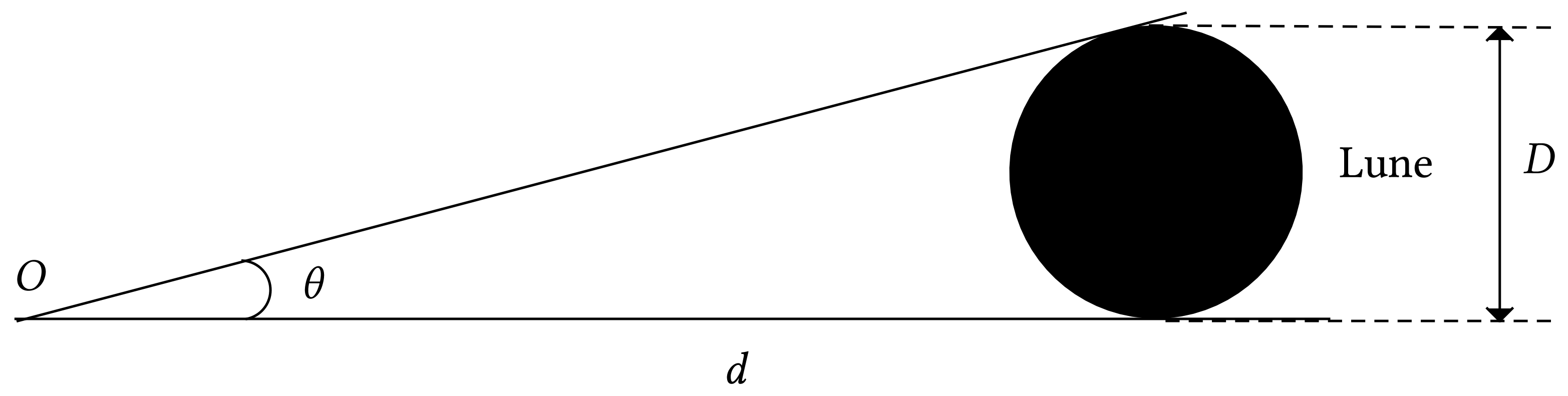
Vue les valeurs des distances, on peut écrire

donc
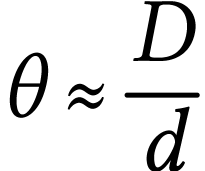
A.N.  .
.
 . L'image
intermédiaire donnée par l'objectif a pour
diamètre
. L'image
intermédiaire donnée par l'objectif a pour
diamètre 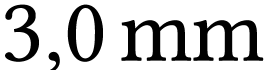 . Quelle
est la vergence de l'objectif ?
. Quelle
est la vergence de l'objectif ?



On constate sur le schéma que l'angle sous l'angle on voit la
Lune est aussi l'angle sous lequel on voit l'image 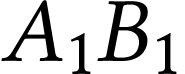 depuis
depuis 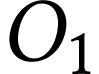 . On a donc
. On a donc
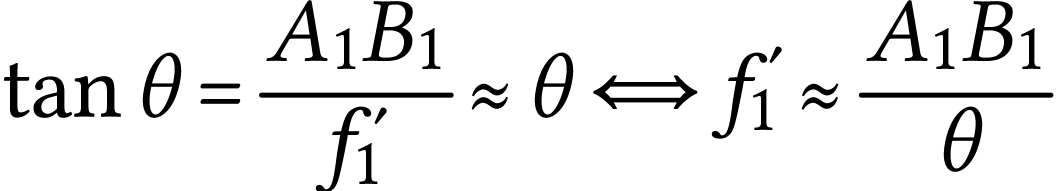
A.N. 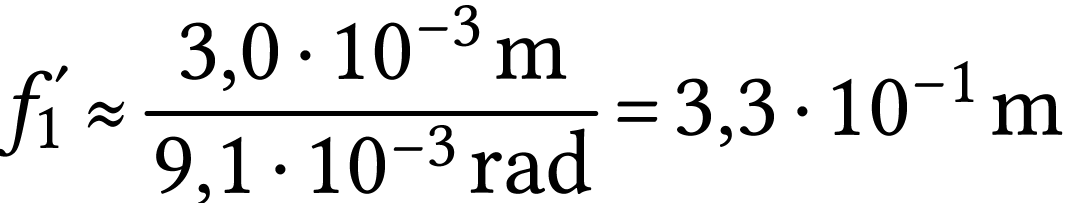 .
.
La vergence de l'objectif vaut donc  .
.


Puisque la lunette est afocale (elle forme une image à
l'infini d'un objet à l'infini), l'image intermédiaire
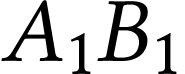 se trouve dans le plan focal image de
se trouve dans le plan focal image de  et dans le plan focal objet de
et dans le plan focal objet de  . Ceci impose que
. Ceci impose que 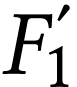 , le foyer image de
, le foyer image de  , soit confondu avec
, soit confondu avec  le
foyer objet de
le
foyer objet de  .
.
On
a donc
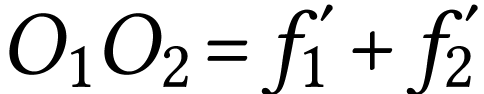
A.N.  .
La distance
.
La distance 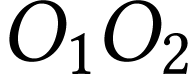 vaut
vaut 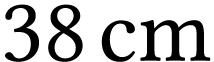 .
.



L'angle sous lequel on voit la Lune à travers la lunette est
 . On constante que c'est
aussi l'angle sous lequel on voit l'objet
. On constante que c'est
aussi l'angle sous lequel on voit l'objet 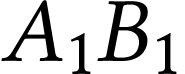 depuis
depuis 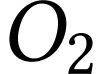 . On a donc
. On a donc
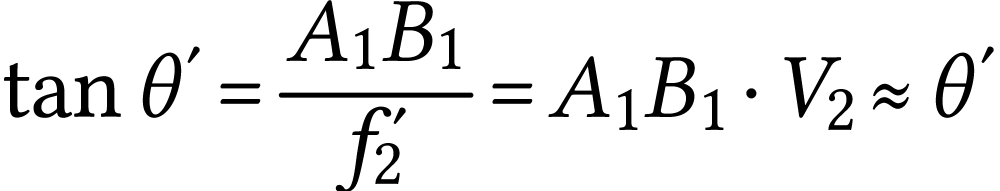
A.N. 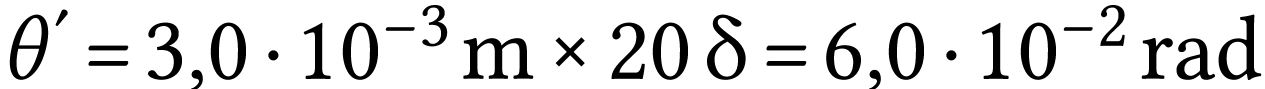
Remarque. 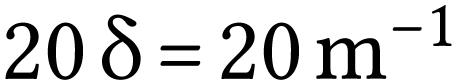 .
.


Par définition le grossissement a pour expression,
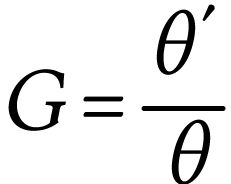
A.N. 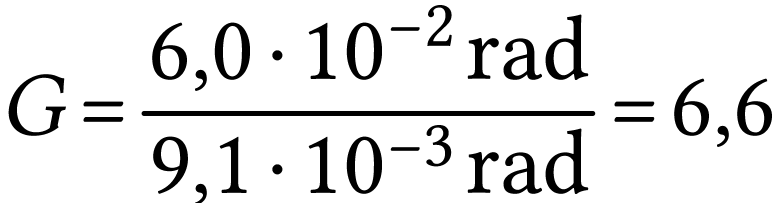 .
La lunette grossit pratiquement 7 fois.
.
La lunette grossit pratiquement 7 fois.
Remarque. Dans le cours on a montré que
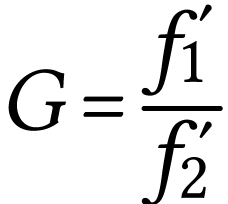
A.N.  .
On retrouve bien la même valeur.
.
On retrouve bien la même valeur.
En 1611, KEPLER propose le principe de la lunette astronomique, avec des lentilles convergentes pour l'oculaire et l'objectif. Il améliore la lunette de GALILÉE, mais l'image est renversée. KEPLER ne mettra cependant pas son idée en pratique ; il faudra attendre 1617 pour voir apparaître les premières lunettes astronomiques.
On se propose de modéliser une lunette astronomique à l'aide de deux lentilles convergentes :
une lentille  de distance focale
de distance focale  ;
;
une lentille  de distance focale
de distance focale  .
.

 .
.



A.N.  .
.
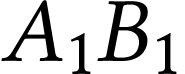 ,
,
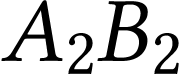 et
et 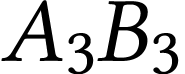 ,
tous de hauteur
,
tous de hauteur 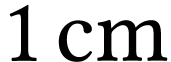 ,
situés en amont de la lentille
,
situés en amont de la lentille  à
à
 ,
, 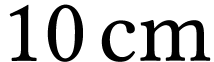 et
et  . Indiquer les positions
et caractéristiques des images
. Indiquer les positions
et caractéristiques des images 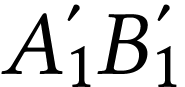 ,
,
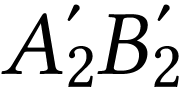 et
et  ,
soit par le calcul ou à partir de constructions
géométriques.
,
soit par le calcul ou à partir de constructions
géométriques.


La relation de conjugaison appliquée à la lentille
 donne
donne
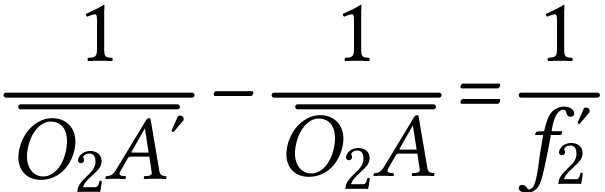
pour un objet  présent n'importe
où sur l'axe. On a donc
présent n'importe
où sur l'axe. On a donc
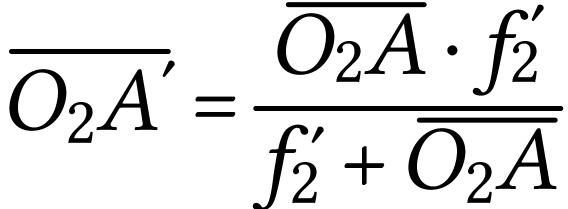 |
(1) |
De plus, par définition, le grandissement a pour expression

ou, dans le cas des lentilles minces convergentes,
 |
(2) |
En combinant (1) et (2), on peut écrire
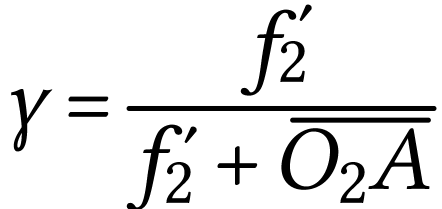 |
(3) |
Pour l'objet 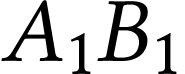 ,
, 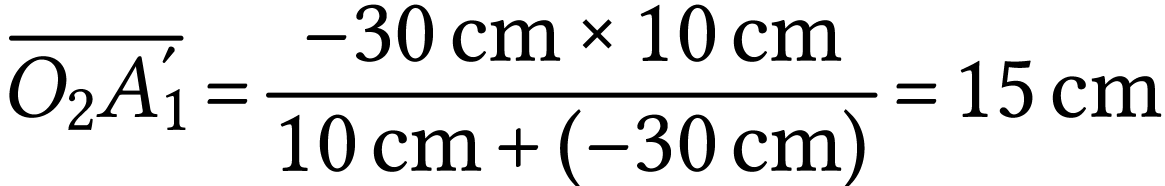 et
et 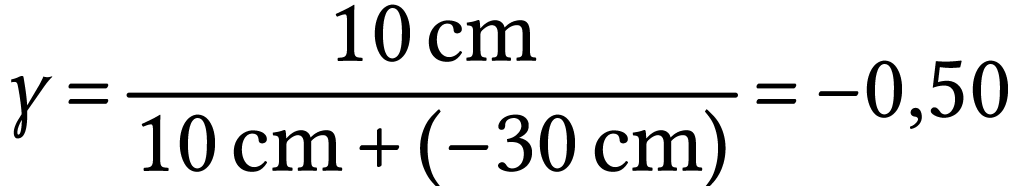 .
L'image se trouve à 15 cm après la lentille (elle
est réelle), est renversée et deux fois plus
petite que l'objet.
.
L'image se trouve à 15 cm après la lentille (elle
est réelle), est renversée et deux fois plus
petite que l'objet.
Pour l'objet 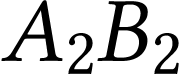 ,
l'image est rejetée à l'infini puisque l'objet est
dans le plan focal objet de la lentille.
,
l'image est rejetée à l'infini puisque l'objet est
dans le plan focal objet de la lentille.
Pour l'objet 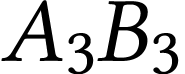 ,
,  et
et 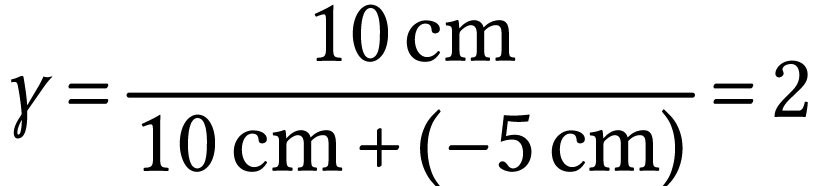 .
L'image se trouve à 10 cm en amont de la lentille (elle
est virtuelle), est droite et deux fois plus grande que l'objet.
.
L'image se trouve à 10 cm en amont de la lentille (elle
est virtuelle), est droite et deux fois plus grande que l'objet.
On reprend la lentille  à laquelle on
associe la lentille
à laquelle on
associe la lentille  ,
placée devant
,
placée devant  , pour
simuler sur le banc d'optique une lunette astronomique utilisée
pour observer un objet
, pour
simuler sur le banc d'optique une lunette astronomique utilisée
pour observer un objet 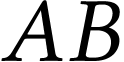 . On
se place dans le cas où l'image intermédiaire
. On
se place dans le cas où l'image intermédiaire 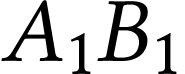 est située dans le plan focal objet de la lentille
est située dans le plan focal objet de la lentille
 .
.
La distance entre les centres optiques des deux lentilles est
fixée à  .
.
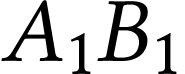 pour la lentille
pour la lentille  ?
?


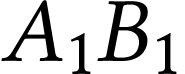 joue le rôle d'objet pour la lentille
joue le rôle d'objet pour la lentille
 .
.
 et
et  ?
?


-  est l'objectif ;
est l'objectif ;
-  est l'oculaire.
est l'oculaire.
la lentille  et son centre optique
et son centre optique 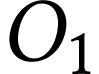 ;
;
les foyers des deux lentilles  et
et  ;
;
l'image intermédiaire 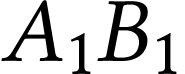 de hauteur
de hauteur  ;
;
le tracé de deux rayons lumineux traversant les deux
lentilles du système optique en passant par  .
.


 ? Où se trouve l'image
définitive
? Où se trouve l'image
définitive  ?
?


 se trouve dans le plan focal image de
l'objectif, l'objet
se trouve dans le plan focal image de
l'objectif, l'objet  se situe donc
à l'infini.
se situe donc
à l'infini.
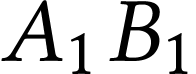 se trouve dans le plan focal objet de
l'oculaire, l'image
se trouve dans le plan focal objet de
l'oculaire, l'image  se situe donc
à l'infini.
se situe donc
à l'infini.
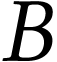 de
l'objet et le diamètre apparent
de
l'objet et le diamètre apparent  de
l'image.
de
l'image.


Le diamètre apparent 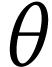 de
de 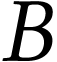 est l'angle sous lequel on voit
est l'angle sous lequel on voit 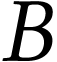 à l'œil nu ;
à l'œil nu ;
Le diamètre apparent  de
de 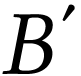 est l'angle sous lequel on voit
est l'angle sous lequel on voit 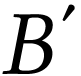 à l'œil nu. C'est aussi l'angle sous lequel on voit
à l'œil nu. C'est aussi l'angle sous lequel on voit
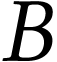 à travers la lunette.
à travers la lunette.


Cf. le graphique.
 en fonction des distances focales des
deux lentilles puis le calculer.
en fonction des distances focales des
deux lentilles puis le calculer.


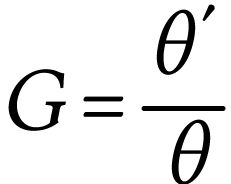
or 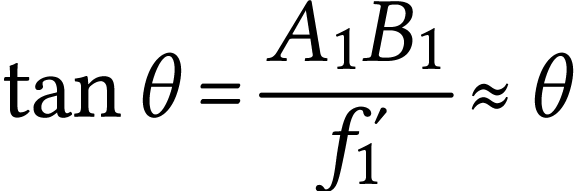 et
et 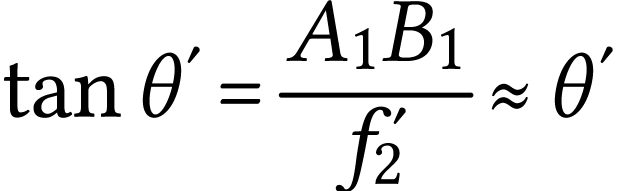 ,
donc
,
donc
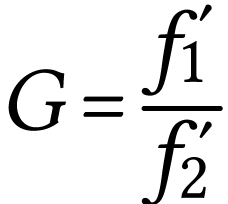
A.N.  .
.


Pour augmenter le grossissement, il faut diminuer la distance focale de l'oculaire ou/et augmenter la distance focale de l'objectif.
Une lunette est constituée de deux lentilles minces : l'objectif
 de distance focale
de distance focale 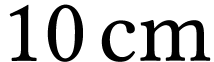 et
l'oculaire
et
l'oculaire  de distance focale
de distance focale 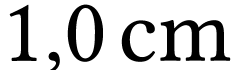 .
.
Avec cette lunette on observe un objet 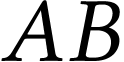 placé à
placé à  de l'objectif ;
de l'objectif ; 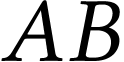 est perpendiculaire à l'axe de la lunette et
est perpendiculaire à l'axe de la lunette et  est situé sur l'axe optique. L'œil est
placé au foyer image
est situé sur l'axe optique. L'œil est
placé au foyer image 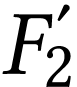 de l'oculaire.
de l'oculaire.
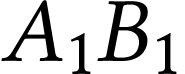 donnée par l'objectif pour que l'œil
n'accommode pas ?
donnée par l'objectif pour que l'œil
n'accommode pas ?


Si l'œil n'accomode pas, cela signifie que l'image de 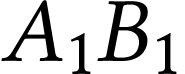 donnée par l'oculaire est à
l'infini. Cet objet est donc situé dans le plan focal objet
de l'oculaire.
donnée par l'oculaire est à
l'infini. Cet objet est donc situé dans le plan focal objet
de l'oculaire.
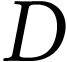 de la
lunette.
de la
lunette.



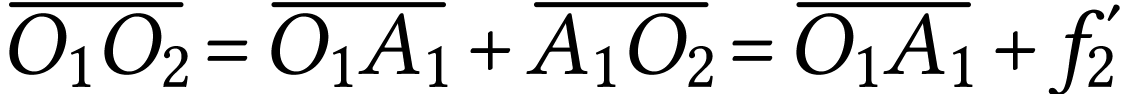
Or
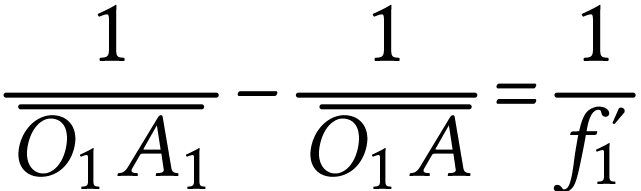
donc
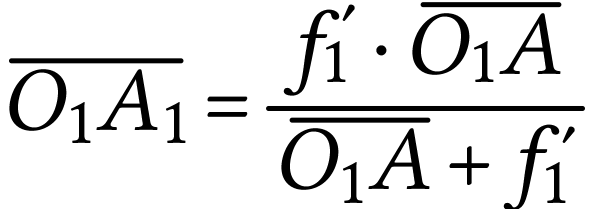
Finalement
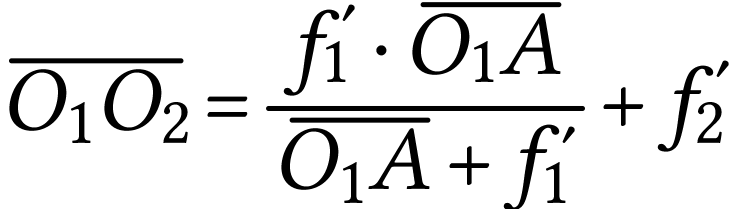
A.N.  .
.
La distance 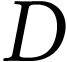 entre les lentilles, calculée
précédemment, est maintenue constante.
entre les lentilles, calculée
précédemment, est maintenue constante.
L'œil placé en 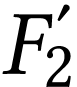 accommode maintenant
au maximum et l'image définitive
accommode maintenant
au maximum et l'image définitive  se forme
à
se forme
à 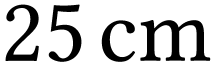 de l'œil :
de l'œil :
Dans ces conditions, on désire calculer la distance  dont il faut déplacer l'objet
dont il faut déplacer l'objet 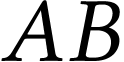 , sans bouger la lunette.
, sans bouger la lunette.
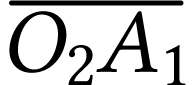 de l'image
intermédiaire
de l'image
intermédiaire 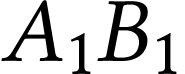 pour obtenir l'image
définitive
pour obtenir l'image
définitive  à
à 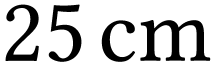 de l'œil.
de l'œil.


La relation de conjugaison appliquée à l'oculaire donne
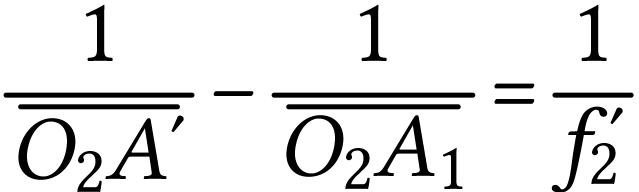
donc
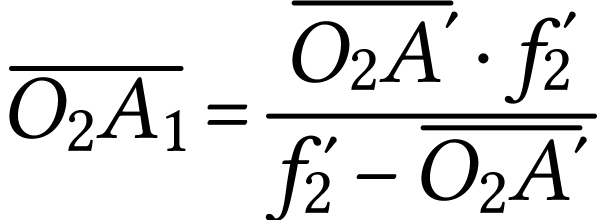
Comme

alors
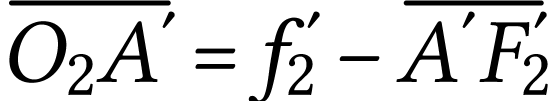
et

A.N.  .
L'objet
.
L'objet 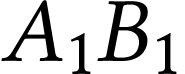 est pratiquement dans le plan focal
objet de l'oculaire, ce qui est normal car
est pratiquement dans le plan focal
objet de l'oculaire, ce qui est normal car  ;
l'image est très loin (pas à l'infini mais pas loin).
;
l'image est très loin (pas à l'infini mais pas loin).
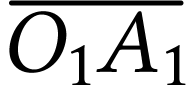 de l'image
intermédiaire
de l'image
intermédiaire 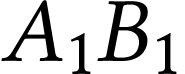 par rapport à la
lentille
par rapport à la
lentille  .
.


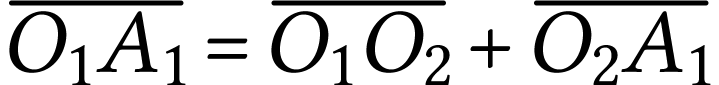
A.N. 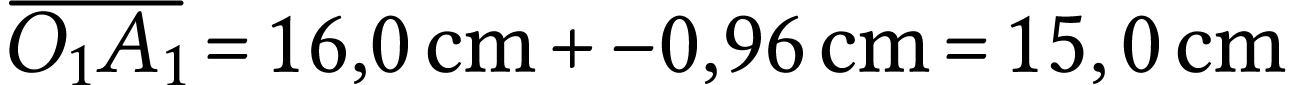 .
.
Remarque. Il est nécessaire ici de conserver tous les chiffres significatifs sur son brouillon car sinon le calcul final ne sera pas possible.
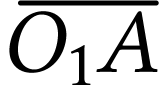 de
l'objet.
de
l'objet.


La relation de conjugaison appliquée à l'objectif donne
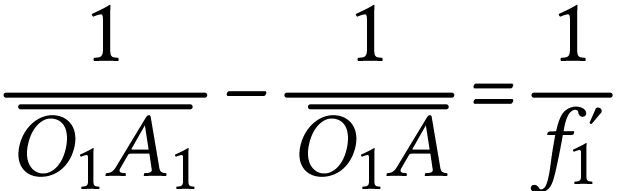
soit

A.N. 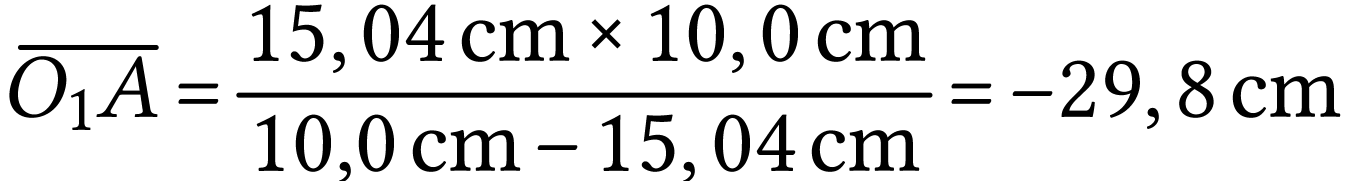 .
.
 dont il faut
déplacer l'objet
dont il faut
déplacer l'objet  pour que l'œil
accommode au maximum.
pour que l'œil
accommode au maximum.


Il a fallu rapprocher l'objet de la lentille d'une distance  égale à 0,2 cm.
égale à 0,2 cm.