Célérité des ondes
électromagnétiques dans le vide : 
; constante de Planck : 
;
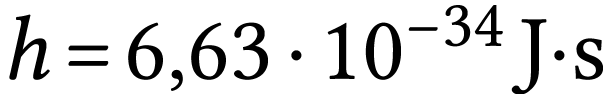électronvolt :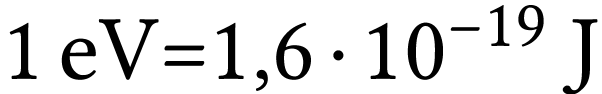 
.
|
Célérité des ondes
électromagnétiques dans le vide :
; constante de Planck : ;
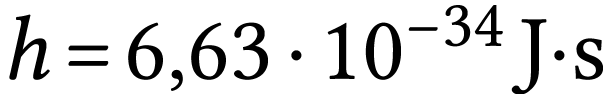électronvolt : .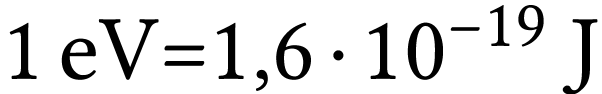
Calculer la période 
d'une onde
électromagnétique de longueur d'onde dans le vide
.
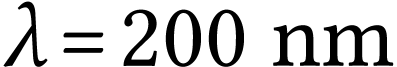Indiquer le
domaine spectral auquel appartient cette onde.
Le système Bluetooth utilise des ondes
électromagnétiques de fréquence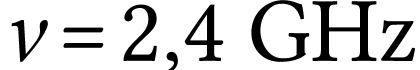 
. Calculer la longueur d'onde dans le vide
de ces ondes électromagnétiques.
Une télécommande classique pour
téléviseur utilise un rayonnement
électromagnétique de longueur d'onde dans le vide
.
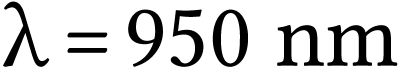À quel domaine spectral appartient cette onde ?
Calculer la fréquence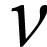 
de la
source émettrice.
Un rayonnement monochromatique rouge possède une longueur
d'onde dans le vide 
égale à
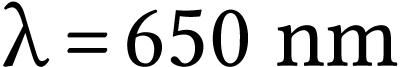. Calculer
l'énergie 
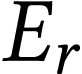, en
joule, puis en électronvolt, du photon associé
à ce rayonnement.
Un photon émis par une source lumineuse possède une
énergie égale à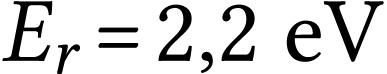 
.
Exprimer cette énergie en joule.
En déduire la fréquence 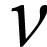et
la longueur d'onde du rayonnement
associé à ce photon.
Vérifier que ce rayonnement appartient bien au domaine des ondes lumineuses.
Une diode électroluminescente émet un faisceau
lumineux monochromatique de puissance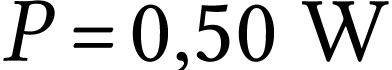 
.
Chaque photon est associé à une onde sinusoïdale
de longueur d'onde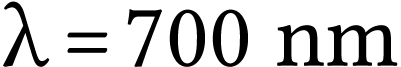 
.
Calculer le nombre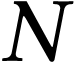 
de photons que la diode
émet chaque seconde.
Puisqu'il est question de longueur d'onde, on peut en
déduire que l'onde est sinusoïdale.
La
période est reliée à la longueur d'onde par
la relation
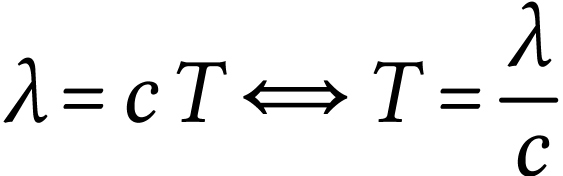
A.N. 
.
Puisqu'il est question de longueur d'onde, on peut en
déduire que l'onde est sinusoïdale.
La longueur
d'onde est reliée à la fréquence par la
relation
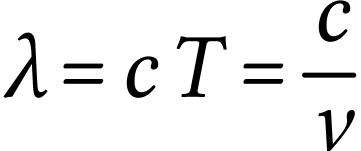
puisque 
.
A.N. 
.
Puisqu'il est question de longueur d'onde, on peut en déduire que l'onde est sinusoïdale.
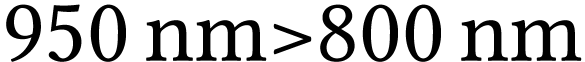, le rayonnement
se situe donc dans l'I.R.
On sait que
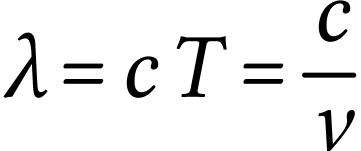
puisque . On a
donc
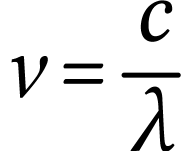
A.N. 
.
Puisqu'il est question de longueur d'onde, on peut en
déduire que l'onde est sinusoïdale. On peut donc
associer un photon d'énergie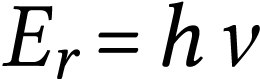 
à cette onde.
Comme
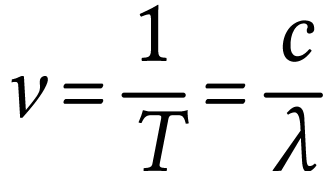
l'énergie 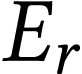s'écrit aussi
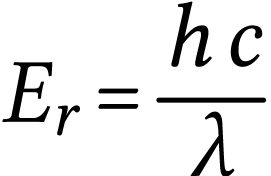
A.N.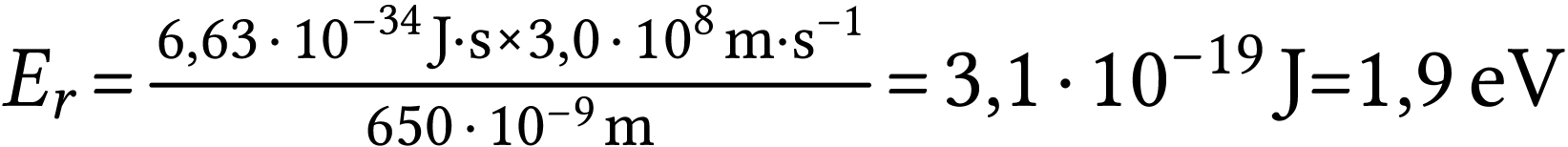 
.
.
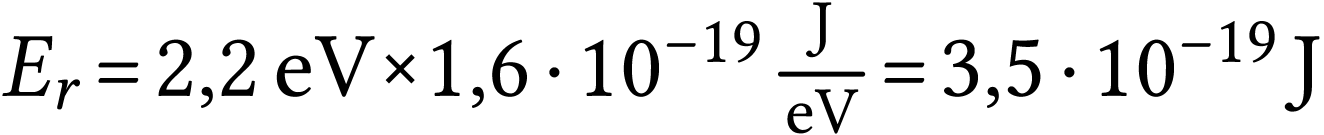Un photon transporte une énergie proportionnelle à la fréquence de l'onde sinusoïdale associée.
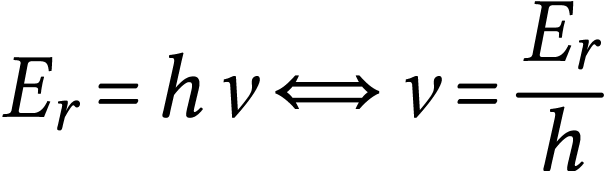
A.N. 
.
La longueur d'onde est reliée à la fréquence par la relation
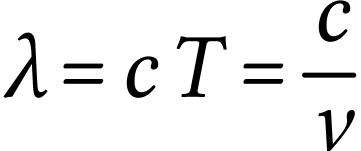
A.N.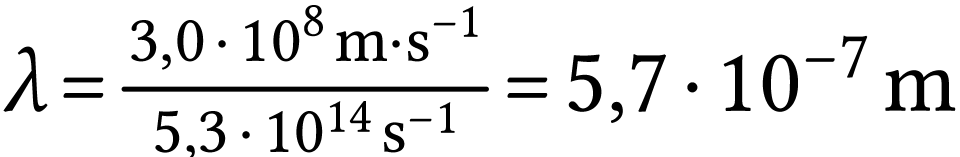 
.
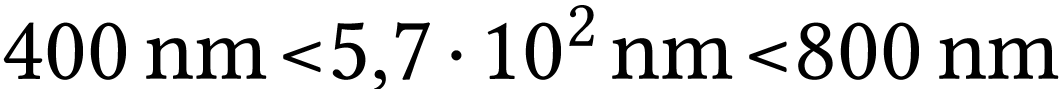, le rayonnement
se situe donc bien dans le visible.
Si on peut considérer la puissance constante au cours, du temps, sa définition est
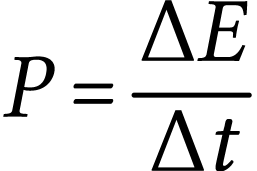
où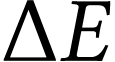 
est l'énergie
échangée pendant la durée 
.
Ici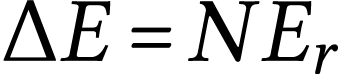 
puisque les 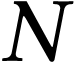photons transportent tous la
même énergie 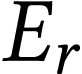(puisque la
source est monochromatique, donc
puisque 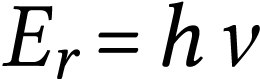et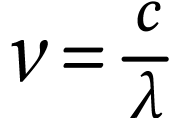 
.
A.N. 
Chaque
seconde la source émet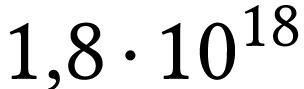 
photons.
Depuis son invention en 1960, le laser à gaz
hélium-néon (He-Ne) est utilisé dans de nombreux
domaines, du bricolage au disque optique. Dans une ampoule contenant un
mélange de gaz (He/Ne), on excite les atomes d'hélium
à l'aide d'une décharge électrique (1 kV). Ils
transmettent leur énergie aux atomes de néon par
collision. Ces derniers se désexcitent en émettant des
radiations de longueur d'onde notée 
.
 |
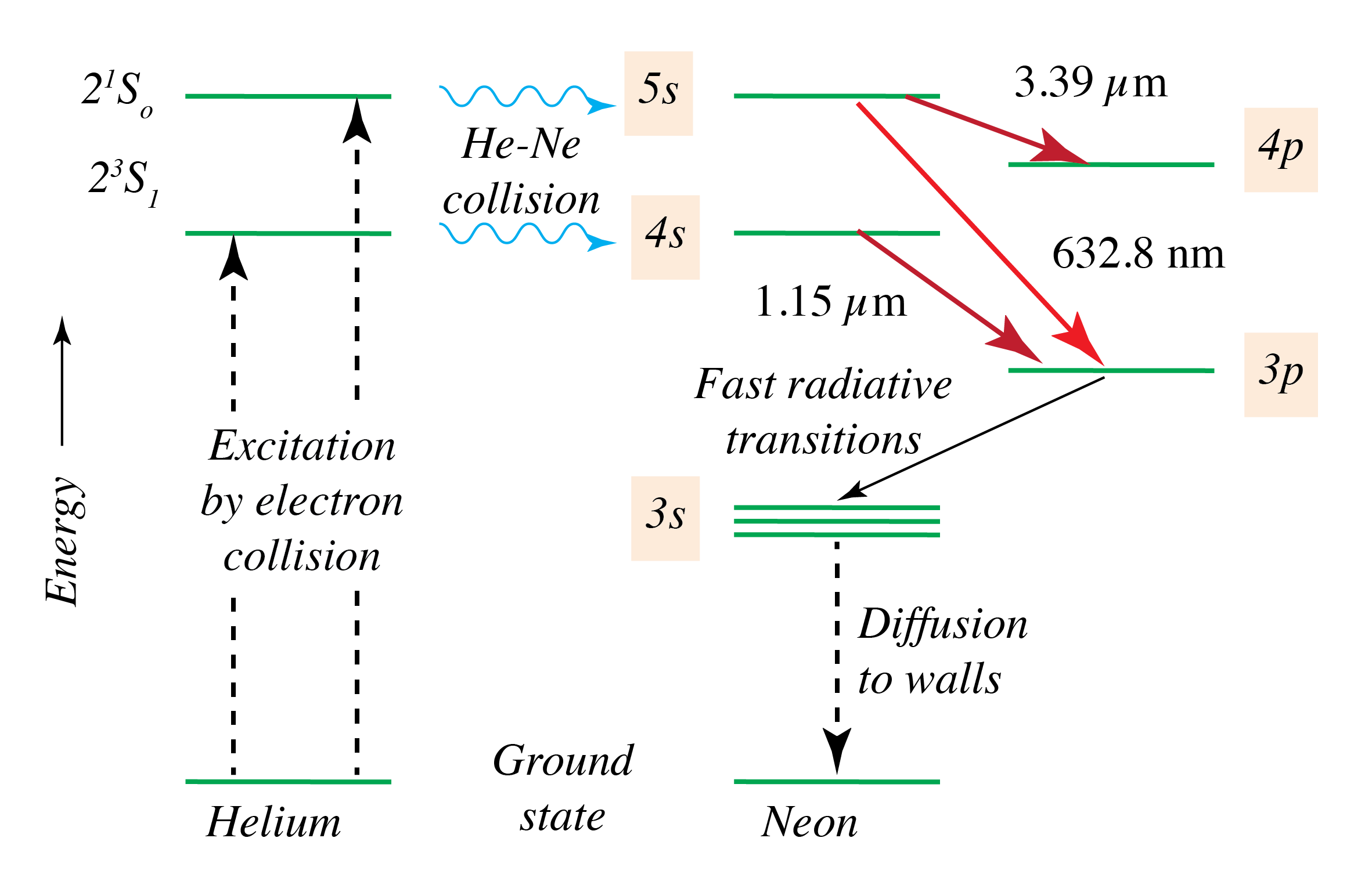Figure 1. (Wikipedia) Les émissions laser sont représentées en rouge. |
Quelle longueur d'onde est susceptible d'être émise ?
Justifier.
On la note par la suite.
Après avoir expliqué les symboles
alphanumériques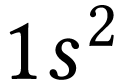 
,
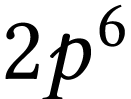, etc., 
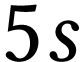, donner la configuration
électronique des atomes d'hélium et de néon
dans leur état fondamental.
Quelle relation relie la longueur d'onde et
sa période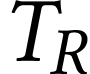 
? Calculer sa valeur
numérique.
Déterminer la valeur de l'énergie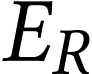 
en joule (J), puis en électron-volt (eV), associée
à la transition.
On peut considérer le niveau d'énergi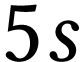e comme référence en posant son
énergie égale à 0 eV. Pourquoi n'est-ce pas
gênant dans les calculs de variations d'énergie ?
En déduire alors, de manière relative, les niveaux
d'énergie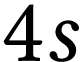 
, 
, 
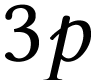de
l'atome de néon.
Représenter les niveaux d'énergie précédents sur un diagramme.
Indiquer la transition à l'origine de l'émission laser.
Selon le document, trois longueurs d'onde sont susceptibles
d'être émises par le laser :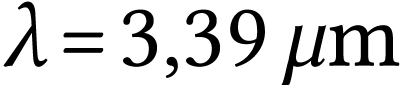 
, 
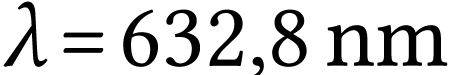et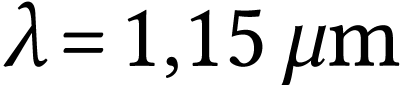 
. Une seule des ces longueurs d'onde se
situe dans le domaine visible, celle susceptible d'être
émise par le laser He-Ne est donc .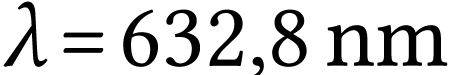
La notation alphanumériques ,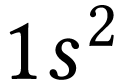
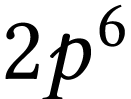, etc., 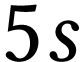permet de décrire la structure du
cortège électronique d'un atome.
L'entier correspond au nombre quantique principal ; il repère la couche électronique dans laquelle se trouve l'électron.
Chaque couche électronique est structurée en
sous-couches repérées par les lettres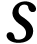 
, 
, 
,
...
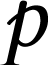Le nombre en exposant à droite du symbole de la sous-couche indique le nombre d'électrons présents dans cette sous-couche.
Pour l'hélium (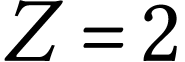
)
la structure du cortège électronique, dans
l'état fondamental, est : ,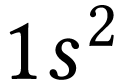
pour le néon (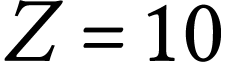
)
la structure du cortège électronique dans
l'état fondamental est :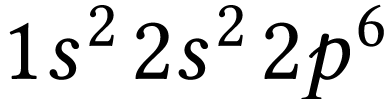 
.
La longueur d'onde de l'onde sinusoïdale associée au photon émis est liée à la période par la relation
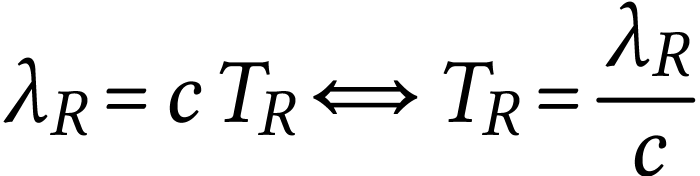
A.N.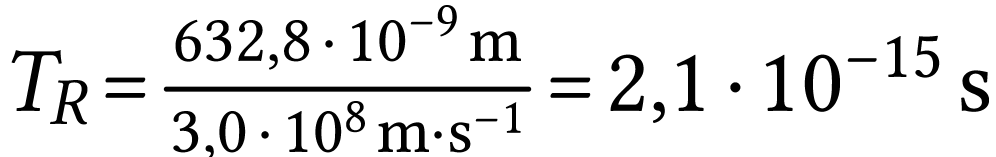 
.
L'énergie transportée par un photon dont l'onde
associée a pour période 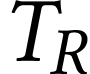a
pour expression
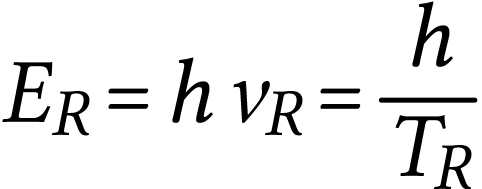
A.N.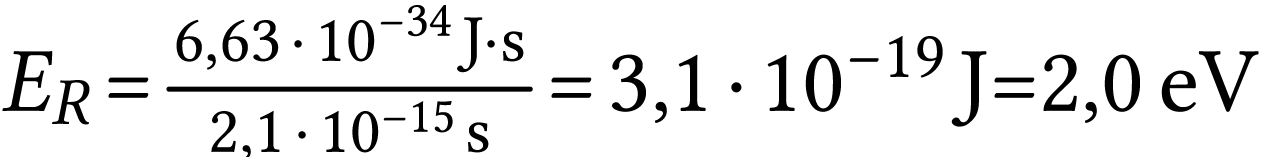 
.
Lorsqu'on considère les énergies potentielles d'interactions, seules les variations ont un sens physique ; ces énergies sont définies à une constante additive près. Peu importe donc le choix de l'origine, tant qu'on ne la modifie pas lors des différents calculs.
L'idée est ici d'exprimer les différences
d'énergies entre les énergies des niveaux
concernés et l'énergie du niveau 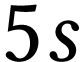. Comme on connait la longueur d'onde
du photon émis lors de cette transition, on peut en
déduire son énergie ; elle est égale
à la différence d'énergie entre les niveaux
concernés.
Remarque. La variation d'énergie du système est négative puisqu'il libère de l'énergie sous forme d'un photon.
On a donc
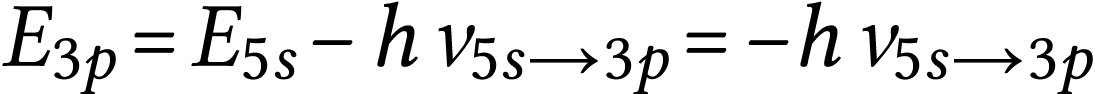
puisque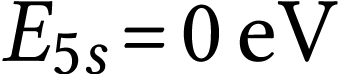 
. Finalement
.
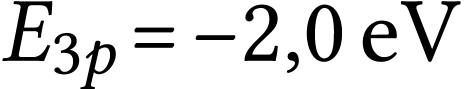De même,
A.N. 
Pour finir,
A.N. 
D'après la réponse à la question 1., la
transition responsable de l'effet laser est la transition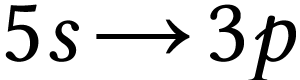 
.