| Décroissance
radioactive, exercices |
|
1Activité et nombre de noyaux
L'iode 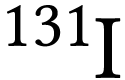 est utilisé en médecine
nucléaire. Sa demi-vie est de 8,1 jours.
est utilisé en médecine
nucléaire. Sa demi-vie est de 8,1 jours.
À l'instant
 , l'activité d'un
échantillon est égale à
, l'activité d'un
échantillon est égale à 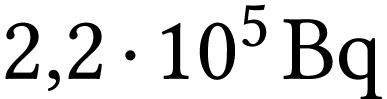 . Donner une estimation du nombre d'atomes
radioactifs présents à cet instant puis après une
année. Conclure.
. Donner une estimation du nombre d'atomes
radioactifs présents à cet instant puis après une
année. Conclure.

 Réponse
Réponse
-
À l'instant initial
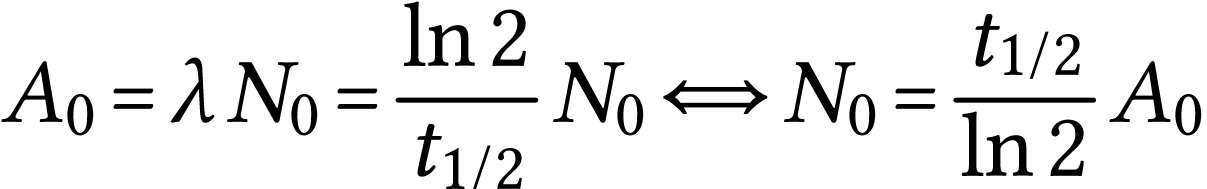
A.N.  .
.
-
Après une année, sachant que
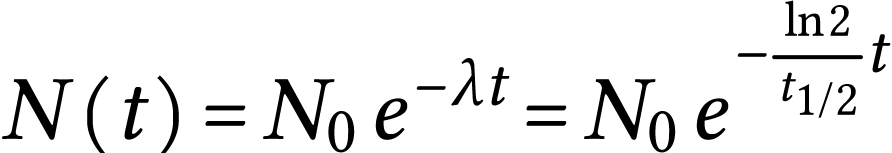
A.N. 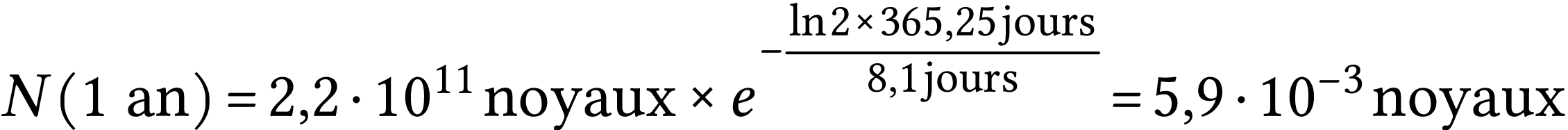 .
.
Cette valeur n'a pas de sens car elle est inférieure à
1 ! Elle indique simplement qu'au bout d'une année, il n'y a
plus de noyaux radioactifs dans cet échantillon.
2Datation au carbone 14
Des fragments d'os et de charbon de bois d'un foyer sont
prélevés dans un site préhistorique. On mesure
l'activité du carbone 14 ( )
des résidus d'os et de charbon, afin de déterminer
l'âge de ces fragments.
)
des résidus d'os et de charbon, afin de déterminer
l'âge de ces fragments.
Le carbone 14 est produit constamment dans l'atmosphère suite au
bombardement de l'azote 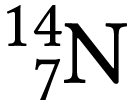 par les neutrons
créés dans la haute atmosphère par les rayons
cosmiques. Les plantes assimilent aussi bien l'isotope
par les neutrons
créés dans la haute atmosphère par les rayons
cosmiques. Les plantes assimilent aussi bien l'isotope  que
que 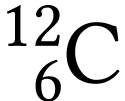 . Les abondances
respectives de ces deux isotopes sont donc les mêmes dans les
composés carbonés de l'atmosphère (
. Les abondances
respectives de ces deux isotopes sont donc les mêmes dans les
composés carbonés de l'atmosphère ( ) et les êtres vivants. À la mort
de ces derniers, il n'y a plus d'assimilation ; le carbone 14 radioactif
se désintègre.
) et les êtres vivants. À la mort
de ces derniers, il n'y a plus d'assimilation ; le carbone 14 radioactif
se désintègre.
Le carbone 14 a une demi-vie
radioactive égale à 5 568 ans.
La mesure de l'activité du carbone 14 contenu dans les fragments
d'os anciens donne 110 désintégrations par heure et par
gramme de carbone. L'échantillon de référence donne
une activité de 13,6 désintégrations par minute et
par gramme de carbone.
1)
Rappeler la définition de la demi-vie radioactive.

 Réponse
Réponse
La demi-vie radioactive 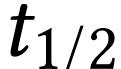 d'un noyau
radioactif est la durée au bout de laquelle l'activité
d'un échantillon constitué de cet isotope est
divisée par deux.
d'un noyau
radioactif est la durée au bout de laquelle l'activité
d'un échantillon constitué de cet isotope est
divisée par deux.
2)
Construire graphiquement la courbe donnant l'activité
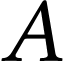
en fonction du temps (en nombre de
désintégrations par minute et par gramme de carbone).
3)
Déterminer, à partir du graphique, l'âge de
l'échantillon.
4)
Montrer que l'âge

de
l'échantillon, exprimé en année, peut être
calculé par la relation
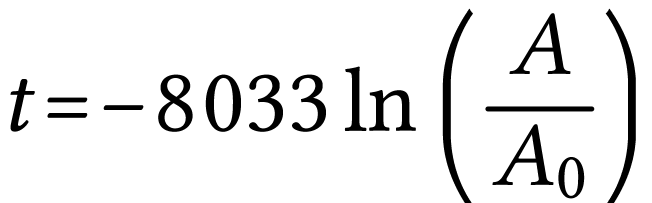 .
.Calculer cet âge.

 Réponse
Réponse
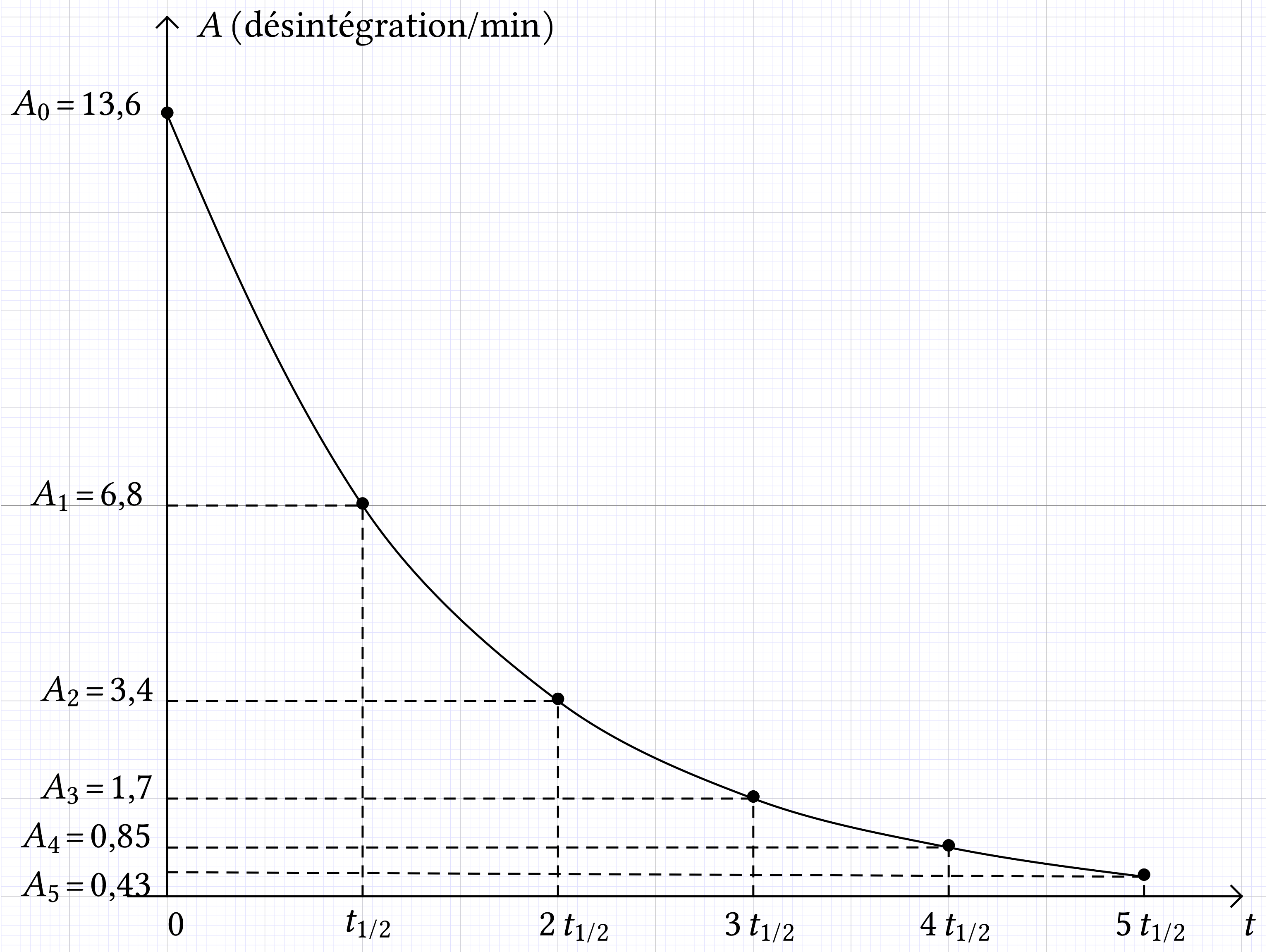
Puisque

et
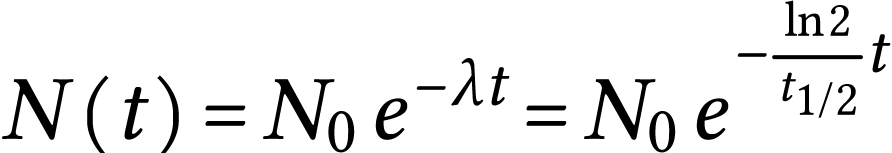
on peut en déduire que

ou

Si on applique la fonction logarithme népérien
à chaque terme de l'égalité, on obtient

ou

A.N.  .
On retrouve bien une valeur comparable à celle
déterminée graphiquement.
.
On retrouve bien une valeur comparable à celle
déterminée graphiquement.
3Émetteur 
Le bismuth 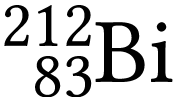 est radioactif ; c'est un
émetteur
est radioactif ; c'est un
émetteur  de demi-vie radioactive
de demi-vie radioactive 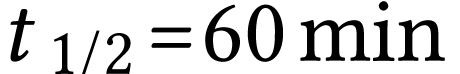 . Cette émission est
accompagnée de l'émission d'un rayonnement
. Cette émission est
accompagnée de l'émission d'un rayonnement  .
.
Données.
1)
Écrire les équations de la désintégration
en les justifiant. Le noyau produit correspond à
l'élément thallium (
 ).
).

 Réponse
Réponse
2)
Calculer la constante radioactive
 .
.
Une source produit  désintégrations
en
désintégrations
en 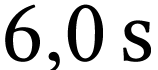 .
.
3)
Quelle est l'activité (supposée constante sur une courte
période) au moment de la mesure ?
4)
En déduire le nombre moyen

de noyaux
radioactifs au moment de la mesure.

 Réponse
Réponse
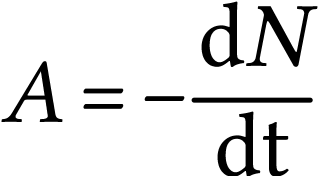
et
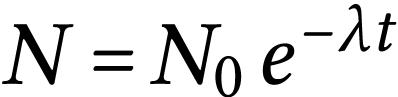
donc
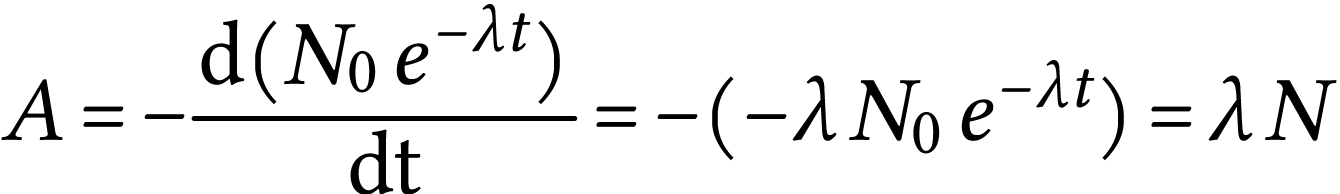
Finalement
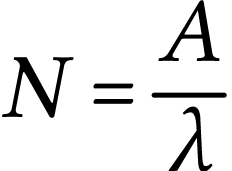
A.N. 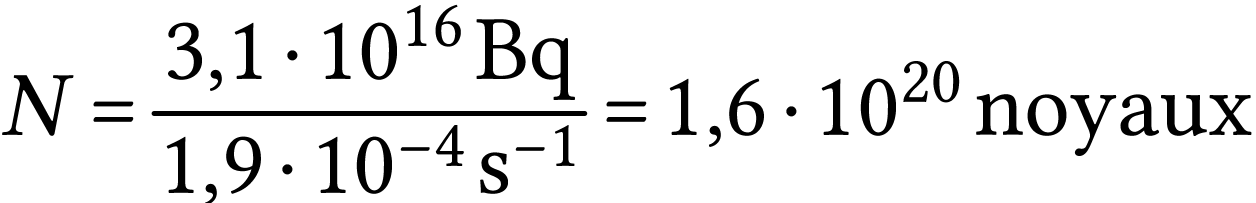 .
.
5)
Déterminer la masse moyenne de bismuth 212 présent dans
la source à cet instant.

 Réponse
Réponse
6)
Calculer le volume d'hélium produit dans les conditions
normales, en 1 minute, en admettant que l'activité reste
constante.

 Réponse
Réponse
Le nombre de noyaux d'hélium créé chaque
seconde est égal au nombre de noyaux de bismuth qui
disparaît. Comme l'hélium est un gaz monoatomique, dans
le modèle du gaz parfait,

A.N. 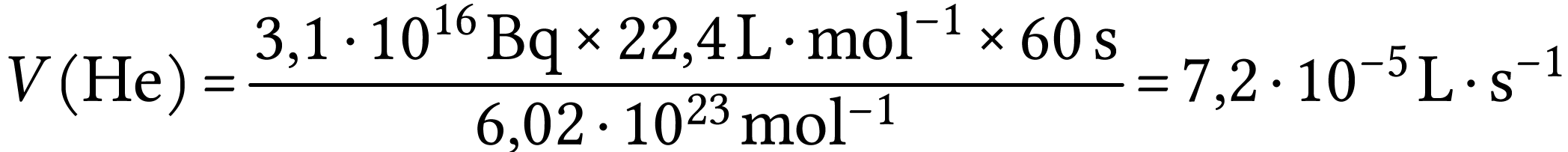 .
.
7)
Quelle sera l'activité de cet échantillon : 1 heure plus
tard ? 1 jour plus tard ?

 Réponse
Réponse
La définition de la demi-vie radioactive est telle que

8)
Quelle devrait être l'activité de cet échantillon
au bout de 60 heures ? Interpréter ce résultat.
Peut-on affirmer que l'échantillon n'est plus radioactif ?
4Émetteur 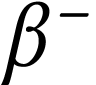
Le cobalt 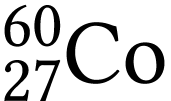 contenu dans les bombes au cobalt
utilisées en médecine est obtenu par le bombardement de
cobalt 59 (seul isotope stable du cobalt) par des neutrons. Le cobalt 60
n'exite pas dans la nature, car il est radioactif
contenu dans les bombes au cobalt
utilisées en médecine est obtenu par le bombardement de
cobalt 59 (seul isotope stable du cobalt) par des neutrons. Le cobalt 60
n'exite pas dans la nature, car il est radioactif 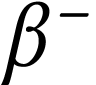 et sa constante radioactive vaut
et sa constante radioactive vaut 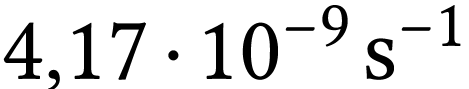 .
Le noyau fils, un des isotopes de l'élément
.
Le noyau fils, un des isotopes de l'élément  se désexcite en donnant deux rayonnements de
longueur d'onde
se désexcite en donnant deux rayonnements de
longueur d'onde 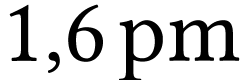 , puis
, puis 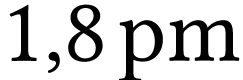 .
.
1)
Quelle est la particule émise lors d'une
désintégration
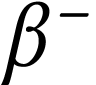
?

 Réponse
Réponse
Lors d'une désintégration 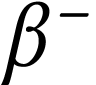 la
particule émise est un électron.
la
particule émise est un électron.
2)
Quel est le type de rayonnement électromagnétique
émis lors d'une désexcitation ?
3)
Pourquoi peut-on parler de radioactivité artificielle dans le
cas du cobalt 60 ?
Pourquoi faut-il se méfier de cette
appellation ?

 Réponse
Réponse
On parle de radioactivité artificielle car l'isotope
radioactif, le cobalt 60 est le produit d'une réaction
nucléaire provoquée, la réaction entre le
cobalt 59 stable et un neutron.
Il ne faut pas laisser penser
que la radioactivité d'un noyau radioactif puisse être
contrôlée ; le cobalt 60 est radioactif, il n'y a aucun
adjectif qualificatif à ajouter.
4)
Écrire l'équation de la réaction de formation du
cobalt 60.

 Réponse
Réponse
5)
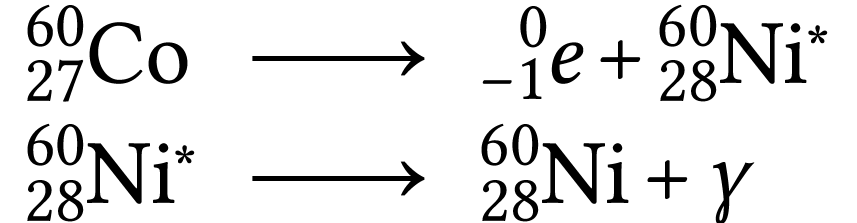
Écrire les équations traduisant la
désintégration du cobalt 60.

 Réponse
Réponse
6)
Calculer la demi-vie radioactive
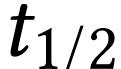
de ce noyau.
Pourquoi le cobalt 60 n'existe-t-il pas dans la nature ?

 Réponse
Réponse
On a montré dans le cours que
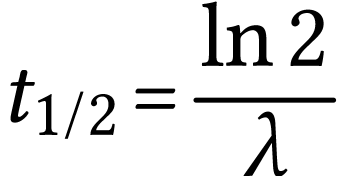
A.N.  .
.
Le cobalt 60 n'existe pas dans la nature car un échantillon
de cobalt 60 a disparu au bout de quelques dizaines d'années.
Les particules 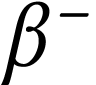 sont émises avec une
énergie cinétique de
sont émises avec une
énergie cinétique de 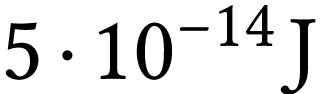 .
Ces particules sont absorbées dans les tissus humains.
.
Ces particules sont absorbées dans les tissus humains.
7)
Quelle est la puissance transférée aux tissus par une
source dont l'activité est de
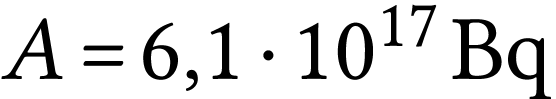
?

 Réponse
Réponse
La puissance transférée est l'énergie
transférée en une seconde. Puisqu'un électron
est libéré chaque fois qu'un noyau de cobalt
disparaît,

A.N.  .
Cette valeur est très importante !
.
Cette valeur est très importante !
5Radioactivité 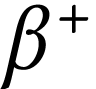
Ce type de radioactivité ne s'observe généralement
qu'avec des éléments artificiels. Les noyaux fils sont
obtenus à l'état excité. Il y a alors
émission de rayonnements  très
énergétiques.
très
énergétiques.
Le brome 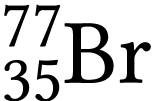 est un émetteur
est un émetteur 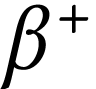 . Sa demi-vie radioactive est de 57 h. Il est
utilisé en imagerie médicale. Le noyau-fils est un isotope
de l'élément sélénium (Se); il peut
émettre un rayonnement
. Sa demi-vie radioactive est de 57 h. Il est
utilisé en imagerie médicale. Le noyau-fils est un isotope
de l'élément sélénium (Se); il peut
émettre un rayonnement  .
.
1)
Écrire les équations traduisant la
désintégration de ce noyau et la désexcitation du
noyau-fils.

 Réponse
Réponse
2)
Calculer la constante radioactive
 .
.

 Réponse
Réponse
On a montré que
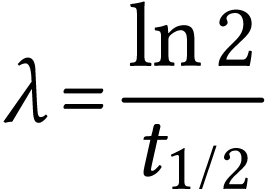
A.N. 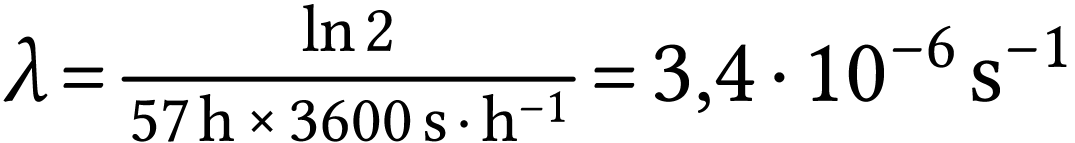 .
.
Un échantillon a une activité initiale de 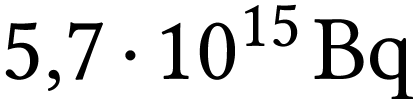 .
.
3)
Calculer le nombre moyen
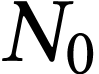
de noyaux au moment
de la mesure.

 Réponse
Réponse
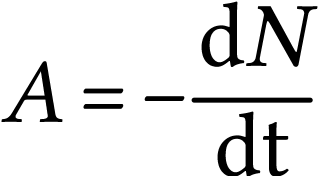
et
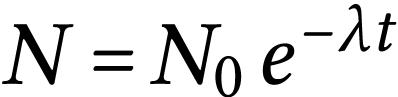
donc
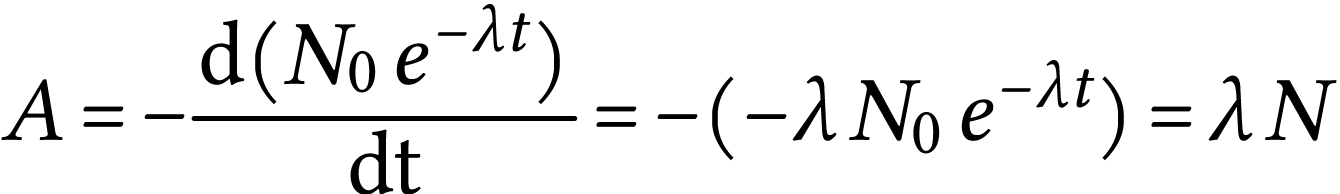
Finalement
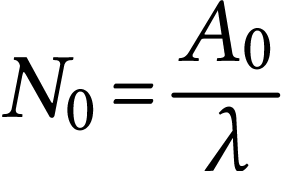
A.N. 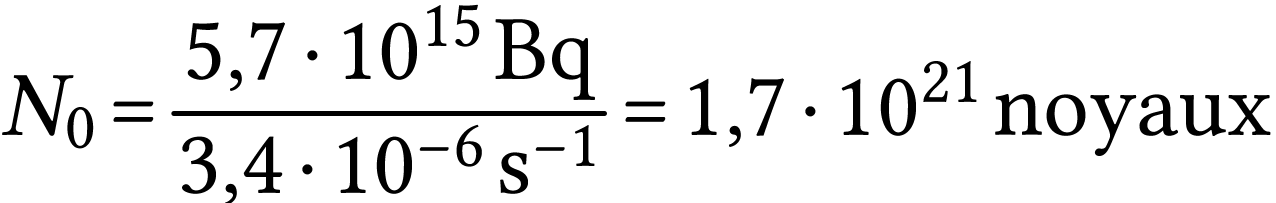 .
.
4)
Les particules
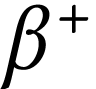
sont émises avec une
énergie cinétique de
 .
.
Toutes les particules émises sont captées par une
feuille d'aluminium. Calculer la puissance fournie à la feuille
d'aluminium.

 Réponse
Réponse
La puissance fournie est l'énergie fournie en une seconde.
Puisqu'un positron est libéré chaque fois qu'un noyau
de brome disparaît,
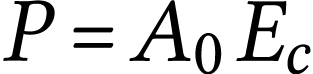
A.N. 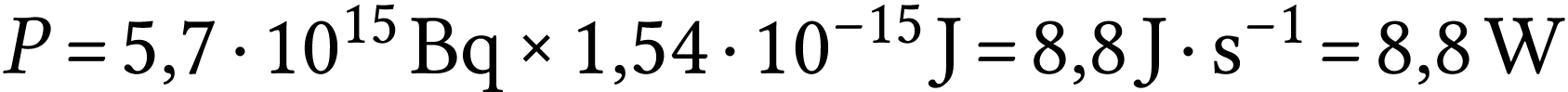 .
.
5)
Un positon se combine avec un électron pour donner deux
rayonnements
 .
.
Écrire la réaction d'annihilation
électron-positron.

 Réponse
Réponse
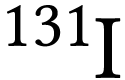 est utilisé en médecine
nucléaire. Sa demi-vie est de 8,1 jours.
est utilisé en médecine
nucléaire. Sa demi-vie est de 8,1 jours. , l'activité d'un
échantillon est égale à
, l'activité d'un
échantillon est égale à 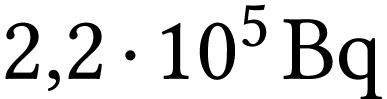 . Donner une estimation du nombre d'atomes
radioactifs présents à cet instant puis après une
année. Conclure.
. Donner une estimation du nombre d'atomes
radioactifs présents à cet instant puis après une
année. Conclure.


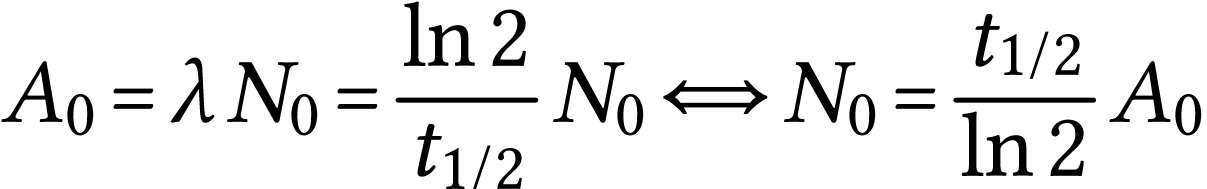
 .
.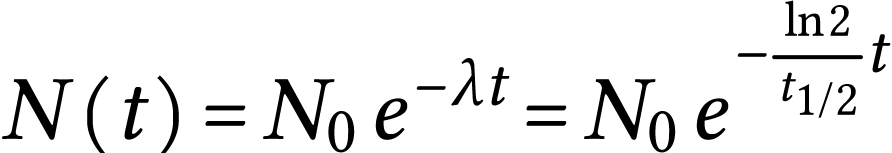
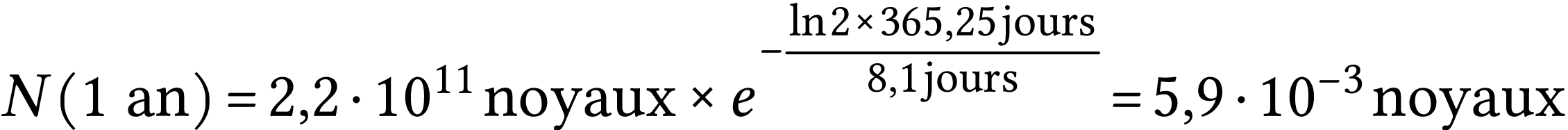 .
. )
)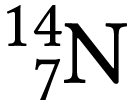 par les neutrons
créés dans la haute atmosphère par les rayons
cosmiques. Les plantes assimilent aussi bien l'isotope
par les neutrons
créés dans la haute atmosphère par les rayons
cosmiques. Les plantes assimilent aussi bien l'isotope 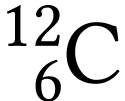 .
. )
)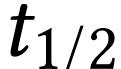 d'un noyau
radioactif est la durée au bout de laquelle l'activité
d'un échantillon constitué de cet isotope est
divisée par deux.
d'un noyau
radioactif est la durée au bout de laquelle l'activité
d'un échantillon constitué de cet isotope est
divisée par deux.
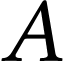 en fonction du temps (en nombre de
désintégrations par minute et par gramme de carbone).
en fonction du temps (en nombre de
désintégrations par minute et par gramme de carbone).
 ,
,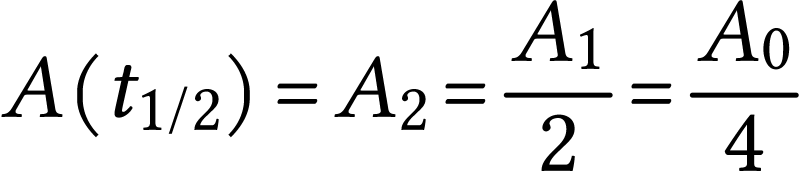 ,
,
 .
.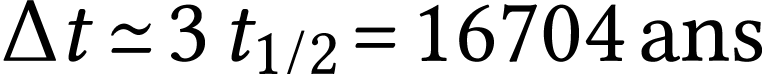 .
. de
l'échantillon, exprimé en année, peut être
calculé par la relation
de
l'échantillon, exprimé en année, peut être
calculé par la relation 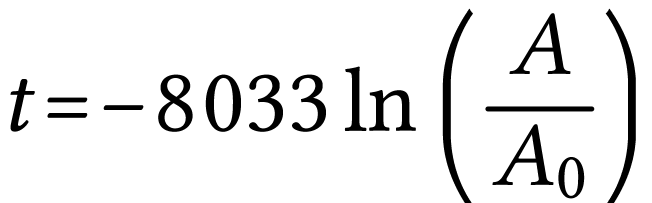 .
.




 .
.
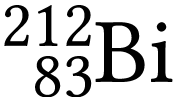 est radioactif ; c'est un
émetteur
est radioactif ; c'est un
émetteur 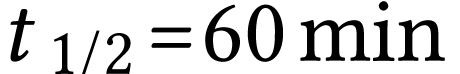 .
. .
. ,
,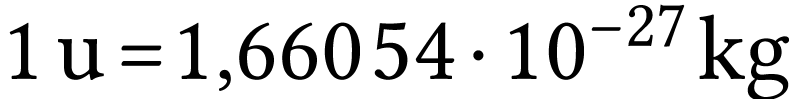 ;
; ;
;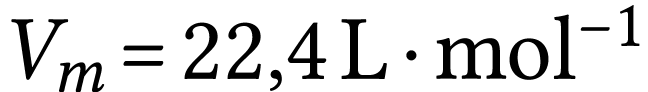 .
. ).
).
 .
.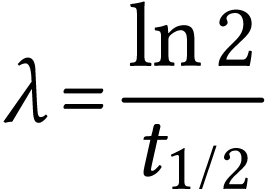
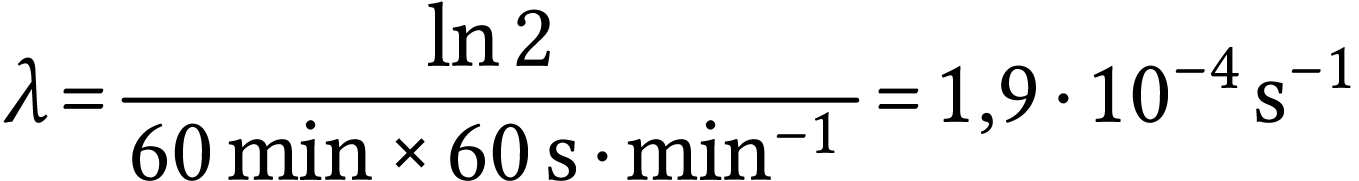 .
. désintégrations
en
désintégrations
en 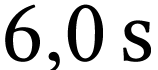 .
.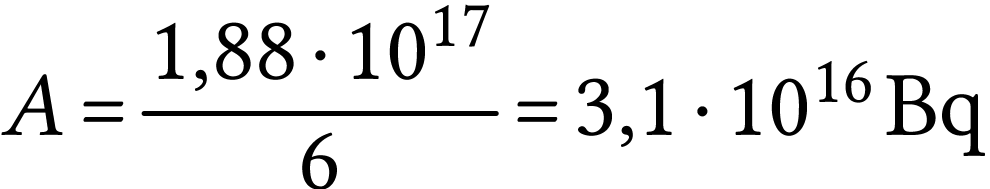 .
. de noyaux
radioactifs au moment de la mesure.
de noyaux
radioactifs au moment de la mesure.
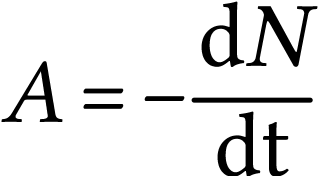
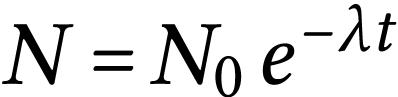
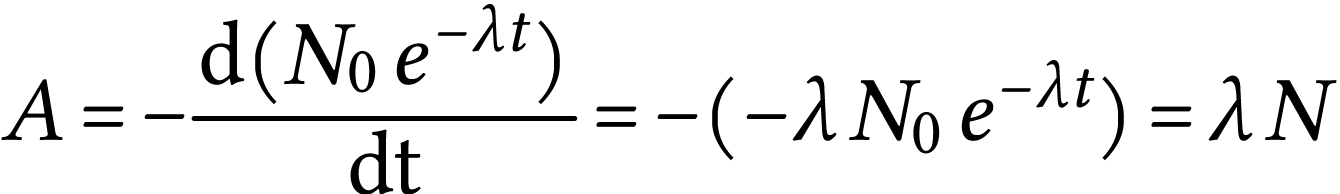
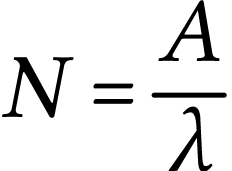
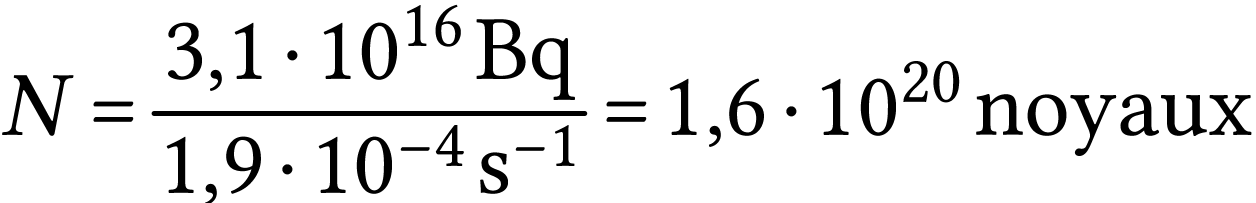 .
.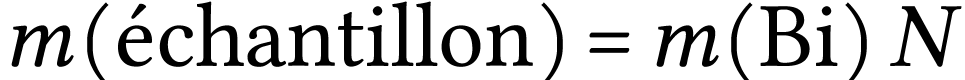
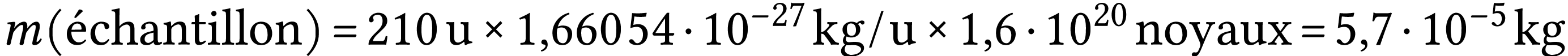 .
.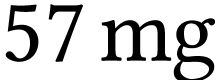 .
.
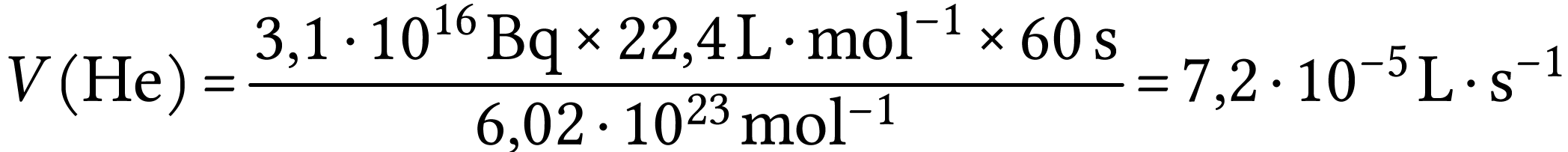 .
.
 ,
,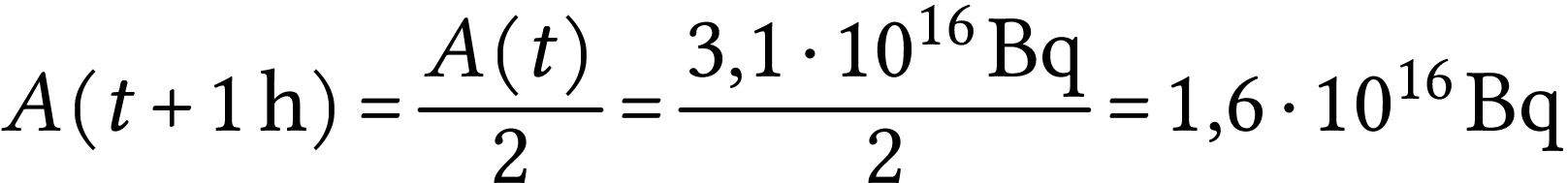 .
. ,
,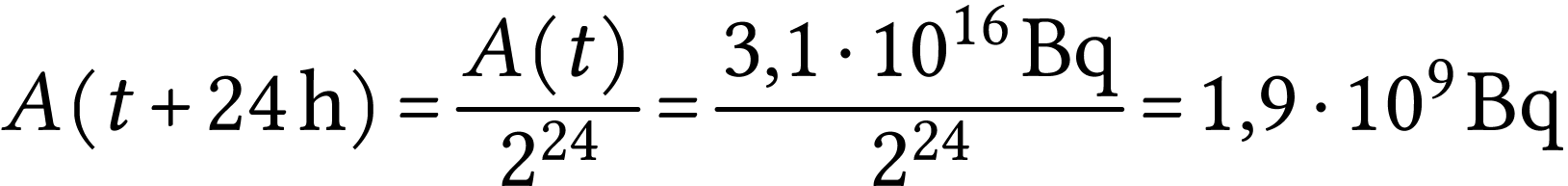 .
. ,
, .
.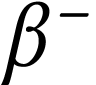
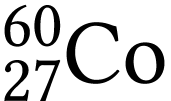 contenu dans les bombes au cobalt
utilisées en médecine est obtenu par le bombardement de
cobalt 59 (seul isotope stable du cobalt) par des neutrons. Le cobalt 60
n'exite pas dans la nature, car il est radioactif
contenu dans les bombes au cobalt
utilisées en médecine est obtenu par le bombardement de
cobalt 59 (seul isotope stable du cobalt) par des neutrons. Le cobalt 60
n'exite pas dans la nature, car il est radioactif 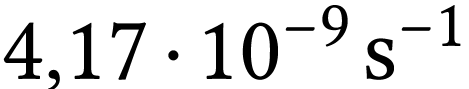 .
. se désexcite en donnant deux rayonnements de
longueur d'onde
se désexcite en donnant deux rayonnements de
longueur d'onde 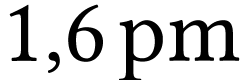 ,
,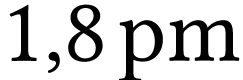 .
.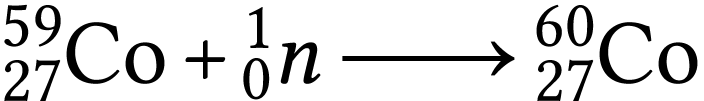
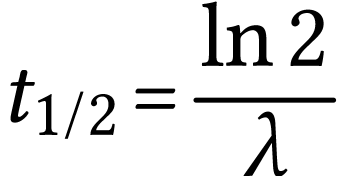
 .
.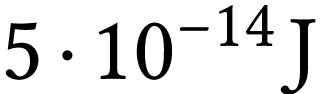 .
.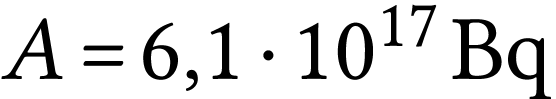 ?
?

 .
.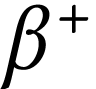
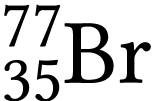 est un émetteur
est un émetteur 
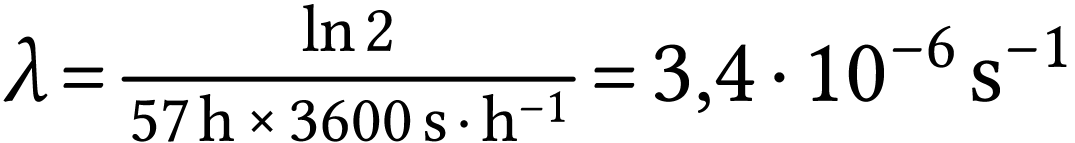 .
.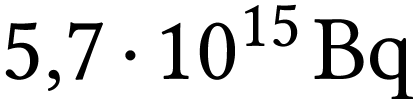 .
.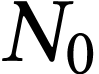 de noyaux au moment
de la mesure.
de noyaux au moment
de la mesure.
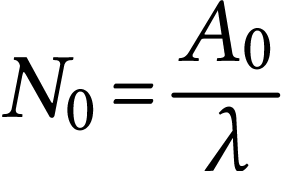
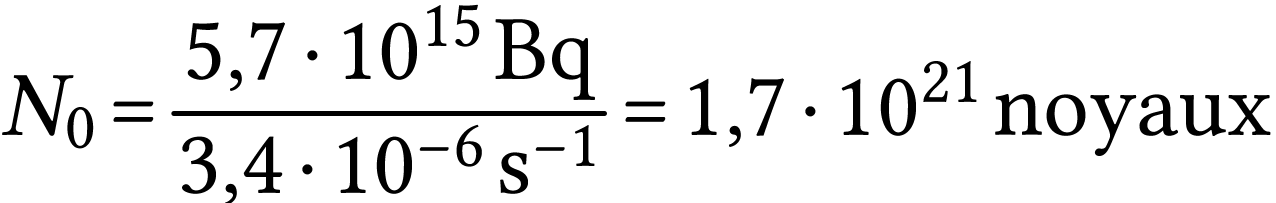 .
. .
.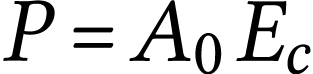
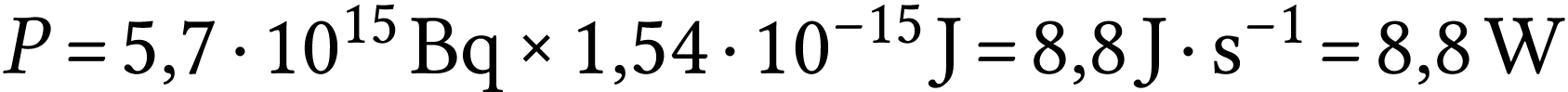 .
.