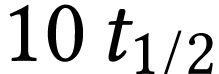 ),
date au-delà de laquelle la détection du carbone 14
devient difficile (en effet
),
date au-delà de laquelle la détection du carbone 14
devient difficile (en effet  ).
).
La décroissance radioactive de certains éléments enfermés dans des roches ou des organismes morts est à l'origine de plusieurs techniques de datation.
La méthode de datation au carbone 14, mise au point dans les années 1950 — Prix Nobel de chimie 1960 pour Willard Frank Libby —, a complètement bouleversé l'archéologie. Grâce à elle, on a pu dater plus précisément les sites et les dessins rupestres (Rupestre : qui est taillé, creusé dans un rocher ou qui est exécuté sur une paroi rocheuse) des peuples primitifs européens, à Stonehenge et Lascaux, par exemple.
Cette méthode est essentiellement utilisée pour dater les
objets de moins de 50 000 ans (environ 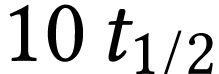 ),
date au-delà de laquelle la détection du carbone 14
devient difficile (en effet
),
date au-delà de laquelle la détection du carbone 14
devient difficile (en effet  ).
).
Le principe de cette méthode repose sur l'hypothèse selon
laquelle le rapport 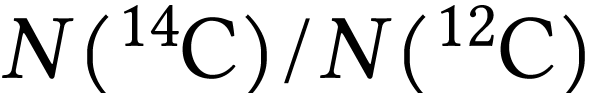 dans
l'atmosphère est, en première approximation,
indépendant du temps. Selon cette hypothèse les noyaux de
carbone 14 sont produits dans la haute atmosphère (à
partir de différentes familles radioactives) à un rythme
constant et il n'y a aucune accumulation car la quantité d'atomes
de carbone 14 qui se désintègrent compense la
quantité produite (en moyenne, on trouve 1 atome de carbone 14
pour 1 000 milliards de carbone 12 dans l'atmosphère).
dans
l'atmosphère est, en première approximation,
indépendant du temps. Selon cette hypothèse les noyaux de
carbone 14 sont produits dans la haute atmosphère (à
partir de différentes familles radioactives) à un rythme
constant et il n'y a aucune accumulation car la quantité d'atomes
de carbone 14 qui se désintègrent compense la
quantité produite (en moyenne, on trouve 1 atome de carbone 14
pour 1 000 milliards de carbone 12 dans l'atmosphère).

Les organismes fixant, finalement, le carbone de l'atmosphère
lors de leur métabolisme — Sans distinction de la
composition isotopique des noyaux présents dans les atomes de
carbone. — contiennent donc les deux isotopes dans les mêmes
proportions que l'atmosphère. Lorsque l'organisme meurt, son
métabolisme cesse et le rapport 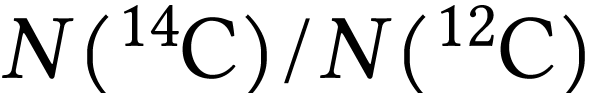 diminue
à cause de la décroissance radioactive du
diminue
à cause de la décroissance radioactive du  . Une mesure précise de
l'activité de l'échantillon ou l'utilisation d'un
spectomètre de masse (cette méthode est
préférée car elle permet d'utiliser des
échantillons plus petits et parce que le résultat de la
mesure est obtenu plus rapidement (environ 1 heure)) permettent de
remonter à l'âge de l'organisme.
. Une mesure précise de
l'activité de l'échantillon ou l'utilisation d'un
spectomètre de masse (cette méthode est
préférée car elle permet d'utiliser des
échantillons plus petits et parce que le résultat de la
mesure est obtenu plus rapidement (environ 1 heure)) permettent de
remonter à l'âge de l'organisme.
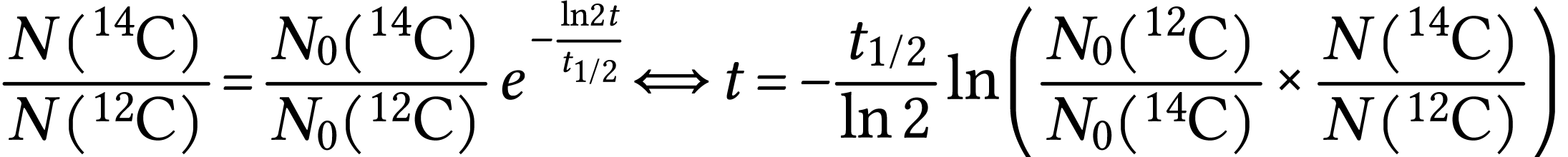
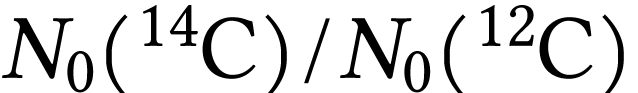 du carbone présent dans
l'atmosphère n'est en fait pas constant : depuis les
débuts de l'ère industrielle l'homme libère du
carbone 12 dans l'atmosphère et les variations du champ
magnétique terrestre, les essais nucléaires en plein
air, etc. modifient la quantité de carbone 14. Il est donc
nécessaire d'adapter le résultat des mesures
effectuées en 1950.
du carbone présent dans
l'atmosphère n'est en fait pas constant : depuis les
débuts de l'ère industrielle l'homme libère du
carbone 12 dans l'atmosphère et les variations du champ
magnétique terrestre, les essais nucléaires en plein
air, etc. modifient la quantité de carbone 14. Il est donc
nécessaire d'adapter le résultat des mesures
effectuées en 1950.
Pour dater des échantillons plus vieux (des roches par exemple), on utilise des noyaux de demi-vie plus longue comme l'uranium 238.
Le produit de désintégration ultime de l'uranium 238
(demi-vie égale à 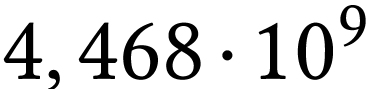 ans)
étant le plomb 206 stable, la mesure du rapport de la teneur
des roches en plomb 206 à celle en uranium 238 permet de
déterminer l'âge des roches anciennes (une roche
contient d'autant plus de plomb qu'elle est âgée).
ans)
étant le plomb 206 stable, la mesure du rapport de la teneur
des roches en plomb 206 à celle en uranium 238 permet de
déterminer l'âge des roches anciennes (une roche
contient d'autant plus de plomb qu'elle est âgée).
Une difficulté subsiste tout de même : la détermination de la quantité initiale de plomb 206 qui s'ajoute à la quantité d'origine radiogénique (Radiogénique : qui prend naissance au cours d'une transformation radioactive). On étudie des minéraux issus de météorites riches en plomb et très pauvres en uranium (sulfure de canyon diablo).
On estime l'âge de la Terre à 4,55 milliards d'années.
Lorsque la composition initiale de l'échantillon en élément radioactif ne peut être connue, on préfère des méthodes comparant l'évolution simultanée de deux types de noyaux différents, comme celle du couple rubidium–strontium.
Le rubidium 87 (27,83% du rubidium naturel) se
désintègre en strontium 87 en émettant des
particules 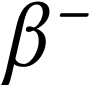 selon l'équation suivante :
selon l'équation suivante :
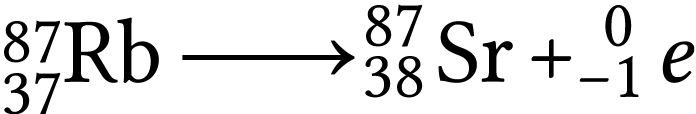
La demi-vie radioactive du rubidium  est de
est de  ans et sa constante radioactive de
ans et sa constante radioactive de 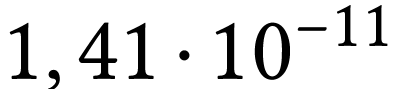 an
an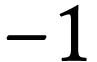 .
.
Un certain nombre de conditions doivent être réunies pour que la méthode Rb-Sr soit applicable, notamment :
l'ensemble des roches ou des minéraux analysés doit
avoir cristallisé à partir d'une source commune de
strontium, c'est-à-dire que les rapports initiaux 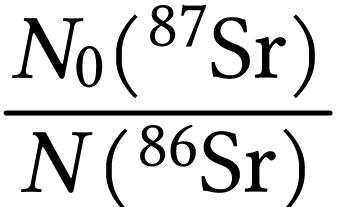 sont égaux.
sont égaux.
le système doit être resté clos depuis sa formation, c'est-à-dire qu'il n'a pas perdu ou gagné de rubidium ou de strontium. Ces échanges sont possibles par exemple si la roche est traversée par des fluides, lorsqu'elle est soumise à un épisode métamorphique, ou encore par altération en surface.
À la fin de la cristallisation d'une roche magmatique, chaque minéral la constituant a intégré des quantités initiales différentes des quatre isotopes du strontium et des deux du rubidium.
On appelle instant initial, noté 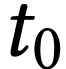 , l'instant de la solidification des minéraux
dans la roche. Les noyaux confinés dans le minéral suivent
évidemment la loi de décroissance :
, l'instant de la solidification des minéraux
dans la roche. Les noyaux confinés dans le minéral suivent
évidemment la loi de décroissance :
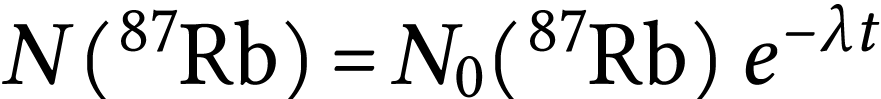 |
(1) |
Dans cette équation le nombre initial de noyaux  est inconnu.
est inconnu.
La méthode des isochrones permet de déterminer le nombre
initial de noyaux et l'âge 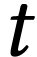 d'un
échantillon.
d'un
échantillon.
Le nombre de noyaux de strontium  formés entre l'instant initial
formés entre l'instant initial 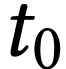 et
l'instant
et
l'instant 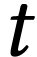 de l'analyse pour datation,
correspond au nombre de noyaux de rubidium
désintégrés, donc à la différence
entre la quantité initiale de
de l'analyse pour datation,
correspond au nombre de noyaux de rubidium
désintégrés, donc à la différence
entre la quantité initiale de  et
celle qu'il reste à la date
et
celle qu'il reste à la date 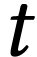 :
:
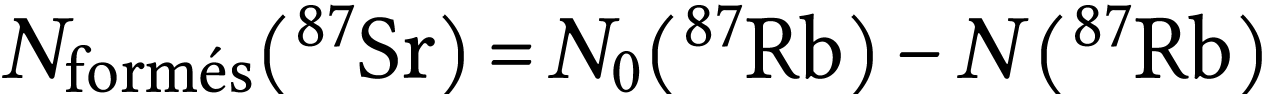 |
(2) |
en utilisant la relation (1) écrite sous la forme : 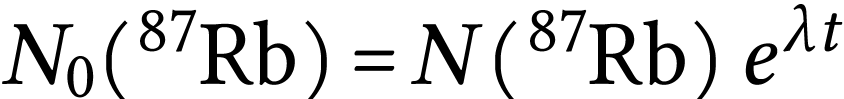 , (2) peut aussi s'écrire :
, (2) peut aussi s'écrire :
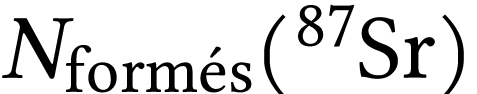 |
 |
 |
|
 |
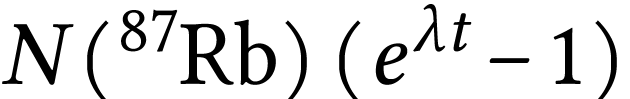 |
Par ailleurs, à l'instant 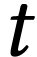 ,
le nombre d'isotopes
,
le nombre d'isotopes  présents dans un
minéral est égal à la somme des noyaux
radiogéniques et des noyaux non radiogéniques
incorporés dans le minéral lors de sa cristallisation
à l'instant initial
présents dans un
minéral est égal à la somme des noyaux
radiogéniques et des noyaux non radiogéniques
incorporés dans le minéral lors de sa cristallisation
à l'instant initial 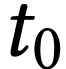 :
:
 |
(4) |
en combinant les relations (3) et (4), il vient :
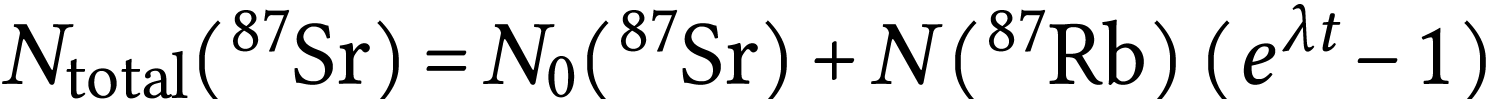 |
(5) |
Par spectrométrie de masse il est plus facile de
déterminer des quantités relatives plutôt que des
quantités absolues d'isotopes. On choisit de mesurer les
teneurs isotopiques par rapport à un isotope de
référence : le strontium 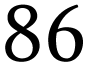 Sr
qui n'est ni radioactif, ni radiogénique. En divisant la
relation (5) par la quantité
Sr
qui n'est ni radioactif, ni radiogénique. En divisant la
relation (5) par la quantité 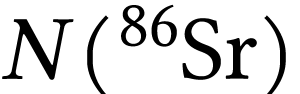 ,
on obtient :
,
on obtient :
 |
(6) |
Pour un minéral, les rapports isotopiques de l'expression (6) sont mesurables à l'instant 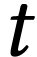 de l'analyse. Le rapport initial
de l'analyse. Le rapport initial 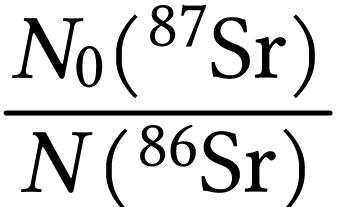 est inconnu
mais à l'avantage d'être commun à tous les
minéraux d'une même roche car il caractérise le
milieu à l'instant de la cristallisation
est inconnu
mais à l'avantage d'être commun à tous les
minéraux d'une même roche car il caractérise le
milieu à l'instant de la cristallisation 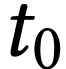 . En revanche, les teneurs en rubidium varient d'un
minéral à l'autre.
. En revanche, les teneurs en rubidium varient d'un
minéral à l'autre.
Remarque. 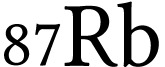 et
et  sont deux isobares, c'est-à-dire deux moyaux
ayant le même nombre de masse mais différant par leurs
nombres de protons. Cela pose un problème en spectrométrie
de masse car les spectromètres de masse utilisés pour la
mesure des rapports isotopiques du Sr ont généralement une
faible résolution, ce qui ne permet pas de séparer
sont deux isobares, c'est-à-dire deux moyaux
ayant le même nombre de masse mais différant par leurs
nombres de protons. Cela pose un problème en spectrométrie
de masse car les spectromètres de masse utilisés pour la
mesure des rapports isotopiques du Sr ont généralement une
faible résolution, ce qui ne permet pas de séparer 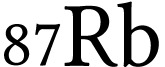 et
et  . Il
est donc indispensable de séparer les deux éléments
avant la mesure au spectromètre de masse, ce qui n'est pas
simple.
. Il
est donc indispensable de séparer les deux éléments
avant la mesure au spectromètre de masse, ce qui n'est pas
simple.
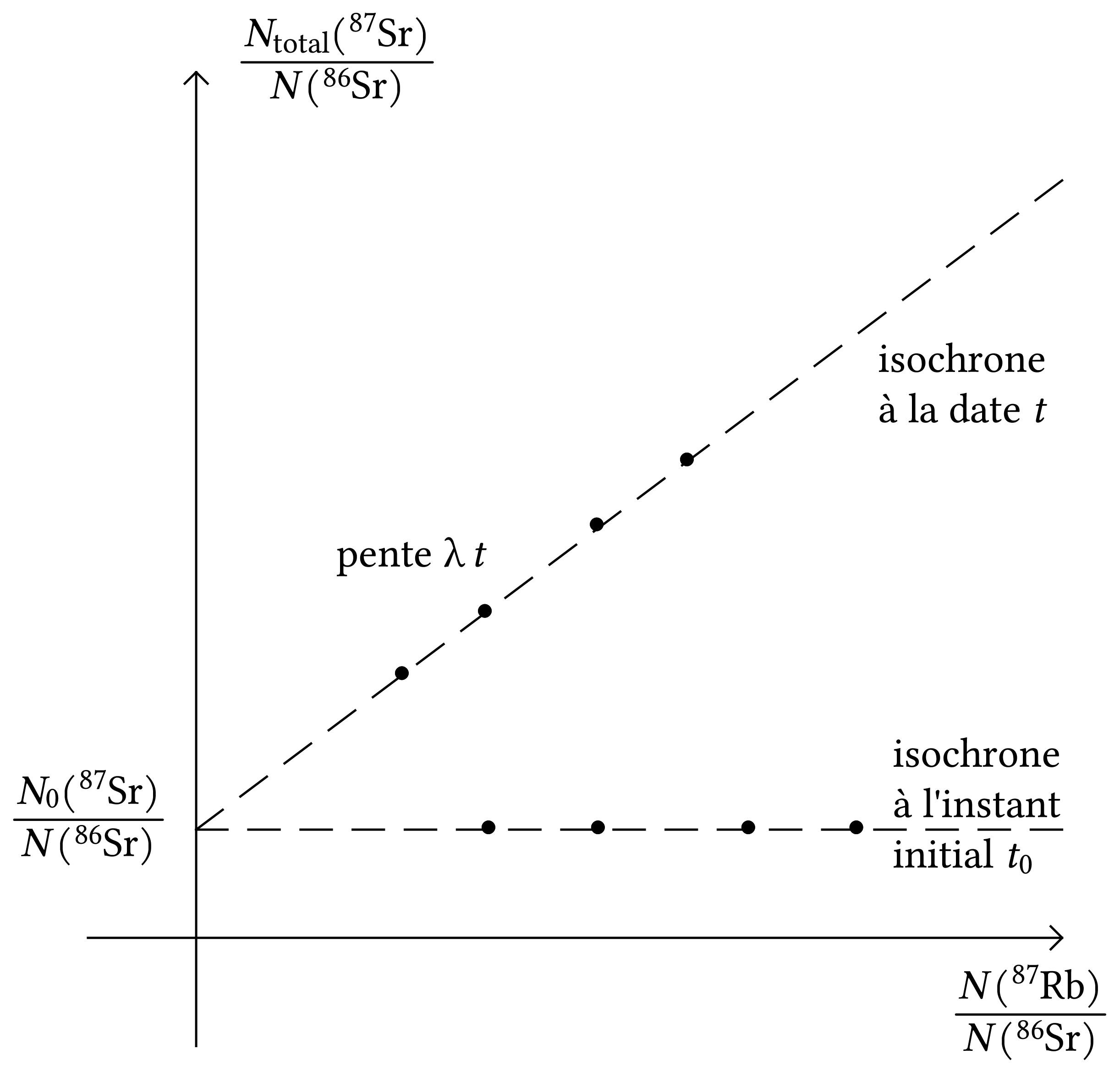
Sur la figure 1, on a représenté les points
correspondant aux mesures effectuées à l'instant 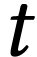 sur quatre minéraux d'une même roche.
Conformément à l'équation (6), les
points sont alignés sur une droite de coefficient directeur
sur quatre minéraux d'une même roche.
Conformément à l'équation (6), les
points sont alignés sur une droite de coefficient directeur 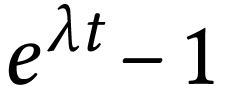 . De plus, l'ordonnée
à l'origine de cette droite est égale au rapport :
. De plus, l'ordonnée
à l'origine de cette droite est égale au rapport : 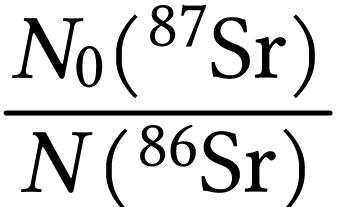 .
.
Il ne reste donc plus qu'à mesurer le coefficient directeur de
cette droite et d'en déduire la date 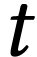 .
.
 |
Comment se fait-il que dans mon cours de SVT, l'exponentielle
n'apparaît pas ?
Comme dit
précédemment, l'âge de la Terre est d'environ
4,55 milliards d'années ; 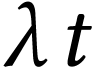 ne
dépasse donc pas 0,065. En mathématique, on peut
démontrer que, si
ne
dépasse donc pas 0,065. En mathématique, on peut
démontrer que, si 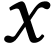 est très
petit,
est très
petit, 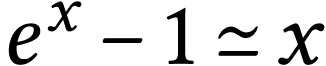 , l'expression
(6) peut donc être simplifiée en :
, l'expression
(6) peut donc être simplifiée en :
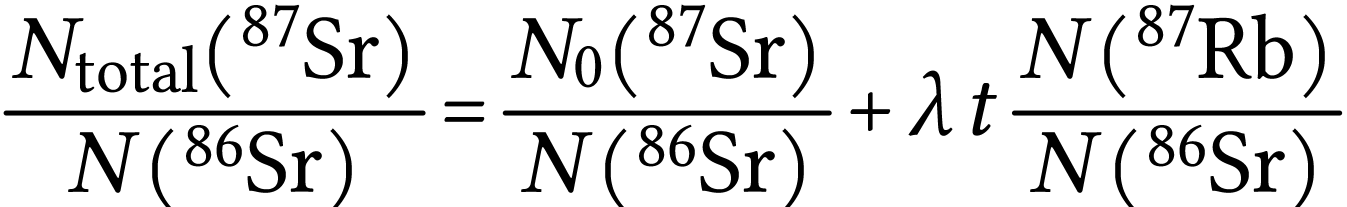 |
(7) |
C'est toujours une relation affine de type 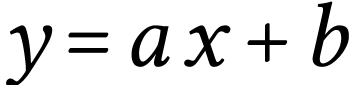 mais le coefficient directeur, d'un point de vue simplement
pratique, est plus simple.
mais le coefficient directeur, d'un point de vue simplement
pratique, est plus simple.