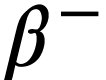.
Soit un échantillon contenant des atomes radioactifs susceptibles de se désintégrer selon l'un des modes définis dans le document d'introduction.
.
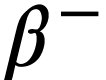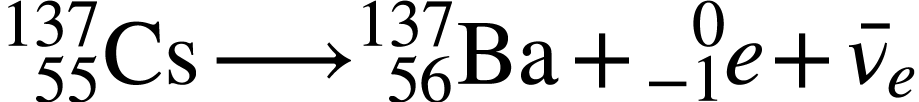
Cette désintégration est de nature probabiliste : c'est
un phénomène aléatoire ;
à chaque instant, il y existe une certaine probabilité
pour qu'un noyau se désintègre entre deux dates
infiniment voisines 
et 
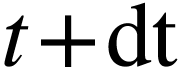. On note cette probabilité 
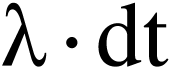où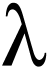 
est une
constante radioactive caractéristique du noyau
considéré et indépendante du temps.
Note. Pour traduire le fait que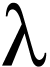 
ne varie pas en fonction de l'âge des noyaux, on dit souvent, de
manière imagée, que les noyaux meurent sans
vieillir : pour les « jeunes », ou pour les «
vieux », la probabilité de se désintégrer est
identique.
Si on considère l'ensemble des noyaux radioactifs
(radionucléides) d'un échantillon, un
détecteur peut compter le nombre de particules émises (par
exemple les électrons) pendant une durée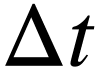 
. On peut alors déterminer
expérimentalement le nombre 
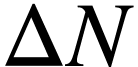de noyaux qui
se désintègrent pendant .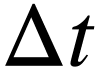
Ce nombre est, en fait, aléatoire, fluctuant autour d'une
valeur moyenne. Aussi, on ne peut pas définir avec
certitude le nombre 
de noyaux existant à
une date . Par contre, on
peut évaluer une valeur moyenne de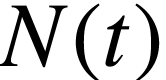 
que nous noterons 
.
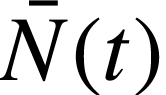Intuitivement, on peut alors admettre qu'entre les dates et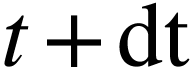 
la variation 
du nombre moyen de noyaux est proportionnelle :
au nombre moyen 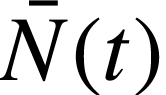de noyaux présents
à la date ;
à la probabilité de désintégration entre
les dates et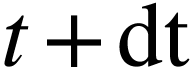
c'est-à-dire : .
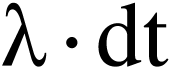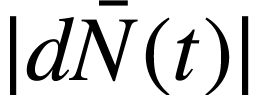de noyaux
qui se désintègrent entre les dates
et .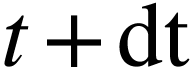
du nombre
moyen de noyaux dans l'échantillon entre les dates et .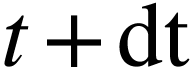
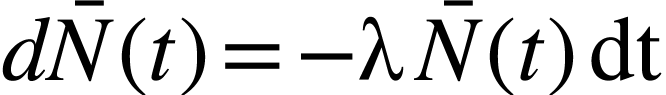
Le signe 
traduit la diminution du nombre de
noyaux.
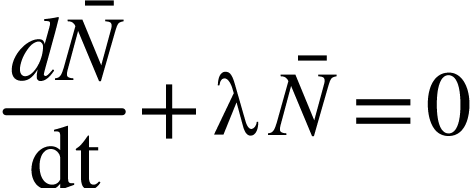
où 
, 
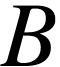et 
sont des constantes.
Déterminer les expressions de ces constantes pour que 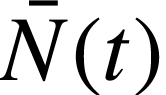soit la solution au problème étudié,
en considérant qu'il existait, dans l'échantillon, 
noyaux à la date 
.
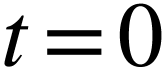Puisque l'expression de 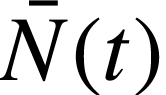donnée
constitue une famille de solutions possibles, elle vérifie
l'équation différentielle pour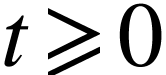 
:
 |
 |
 |
|
 |
|
|
|
 |
|
|
|
 |
|
 |
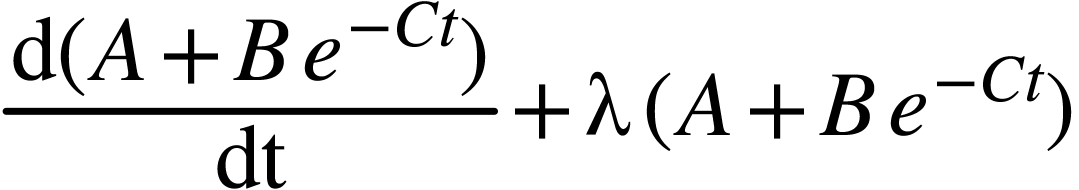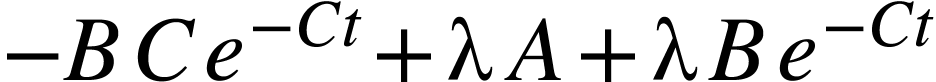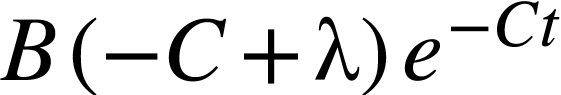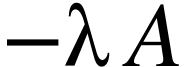Le terme à gauche du signe égal dépend du temps
alors que celui à droite est constant au cours du temps. La
seule possibilité est donc que le terme de gauche soit nul,
pour :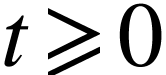
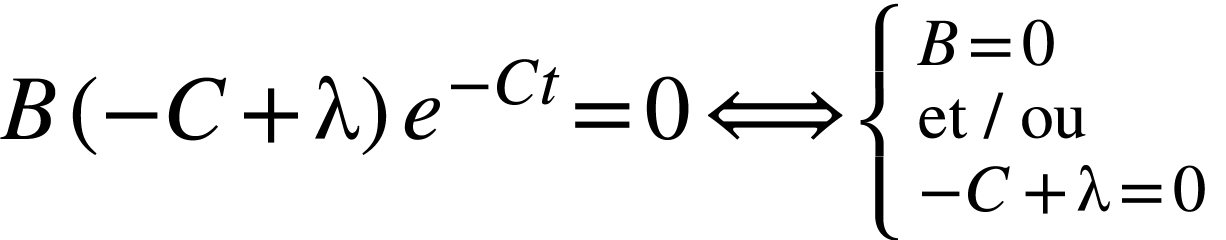
La première solution est impossible, car si 
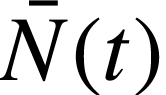, est une constante
au cours du temps ; le nombre de noyaux radioactifs reste constant
au cours du temps !
La solution est donc
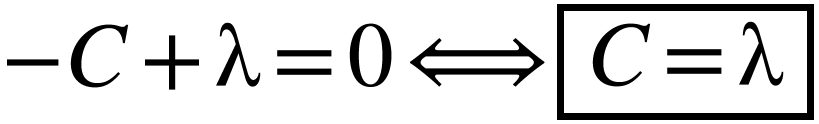
Si on injecte cette solution dans l'équation (1), on obtient
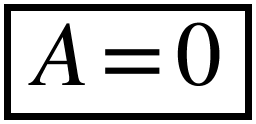
La famille de solutions peut donc s'écrire :
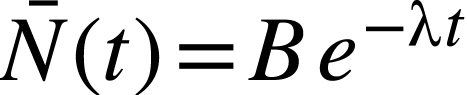
Pour déterminer la solution au problème, il faut prendre en compte la condition initiale :
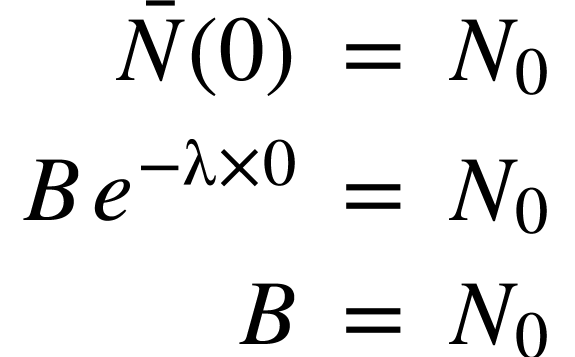
La solution au problème est donc :
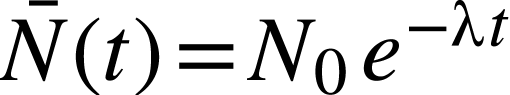
L'évolution du nombre moyen de noyaux est exponentielle, une durée infinie est nécessaire pour complètement éliminer tous les noyaux radioactifs d'un échantillon.
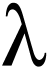? Que
représente-t-elle ?
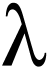est l'inverse d'un temps. C'est la
probabilité de désintégration par seconde pour
une famille de noyaux donnés.
Définition. On appelle demi-vie radioactive
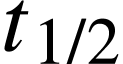la durée au bout de laquelle le nombre
moyen de noyaux radioactifs d'un échantillon a
été divisé par 2 :
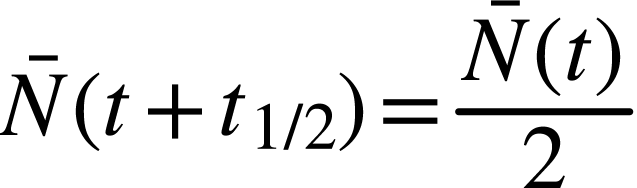
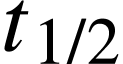en fonction de 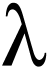. La demi-vie radioactive dépend-elle du
temps ?
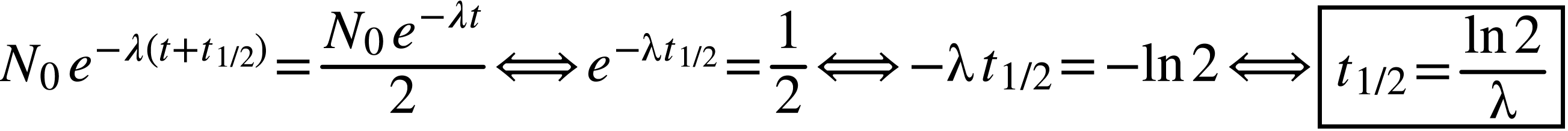
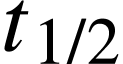et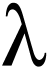
soient inverses l'une de l'autre.
Plus la probabilité de désintégration à chaque seconde est grande, plus la demi-vie est petite.
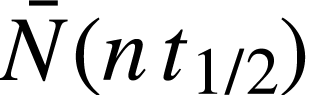de noyaux toujours dans l'échantillon à la date 
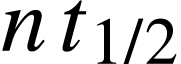et , le
nombre initial de noyaux..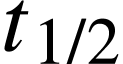
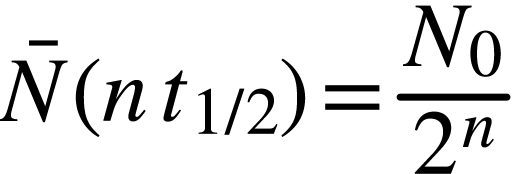
ou, plus généralement,
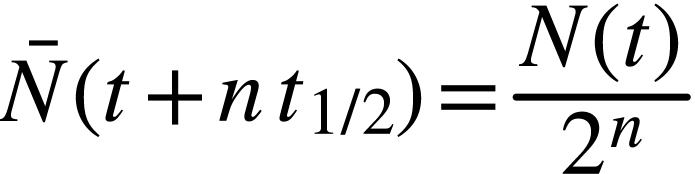
On place le point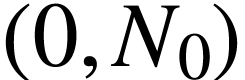 
sur le graphique 
. On place ensuite le point
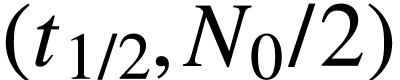, puis le point 
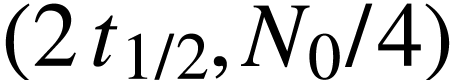, puis le point 
, etc.
Note. La demi-vie radioactive 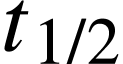, comme la constante radioactive 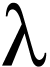, est une caractéristique de la
famille de noyaux radioactifs. Celle du polonium 210 est 138
jours, tandis que celle du bismuth 210 ne dépasse pas 5 jours.
La période du thorium 232 est de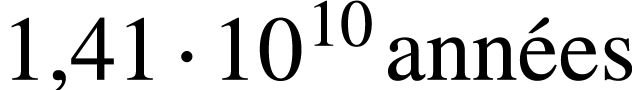 
,
alors que celle du thorium 224 ne vaut que 1,05 s. On classe
habituellement les noyaux en trois catégories :
les noyaux stables ;
les noyaux dont la demi-vie radioactive est de l'ordre de grandeur
de l'âge de la Terre (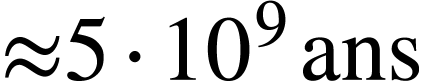
)
et qui, depuis leur formation, n'ont pas eu le temps de tous
disparaître ;
les noyaux de demi-vie radioactive plus courte pour lesquels 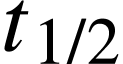varie de quelques années à
quelques microsecondes.
d'un échantillon de noyaux radioactifs.
L'activité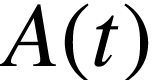 
d'une substance
radioactive, à la date ,
représente le nombre moyen de désintégrations
par seconde.
Note. L'unité de l'activité est le becquerel (symbole Bq) ; elle correspond à une désintégration par seconde.
À chaque instant, un détecteur adapté permet de mesurer le nombre moyen de particules émises par unité de temps, nombre égal au nombre de désintégrations par unité de temps. Un détecteur mesure donc l'activité de l'échantillon, c'est une grandeur expérimentale.
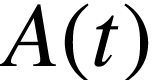en
fonction de 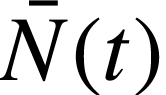. En
déduire que l'activité décroit exponentiellement.
Par définition,
donc
ou
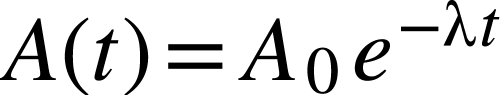
si on pose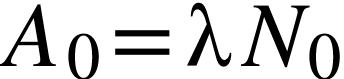 
(activité de
l'échantillon à la date ).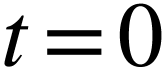
Note.
L'activité est proportionnelle au nombre moyen de noyaux
susceptibles de se désintégrer à la date
.
Elle est d'autant plus grande que la constante radioactive 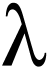est grande, c'est à dire que la demi-vie
radioactive est petite.
Elle décroit très rapidement en début d'émission et voit sa variation diminuer au cours du temps.
La mesure de l'activité à deux dates
différentes permet de déterminer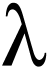
puis d'en déduire .
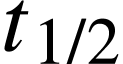On trace généralement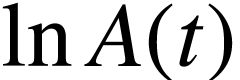 
.
L'évolution de la variation de l'activité au cours du temps s'obtient en étudiant la dérivée de la grandeur par rapport au temps :
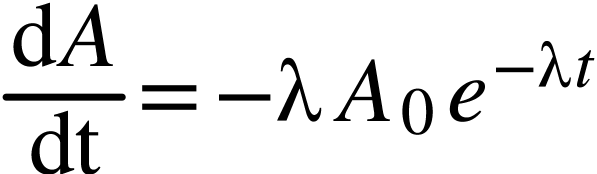
En valeur absolue, on obtient :
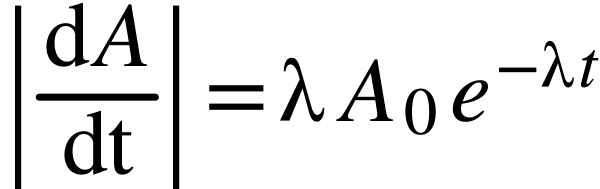
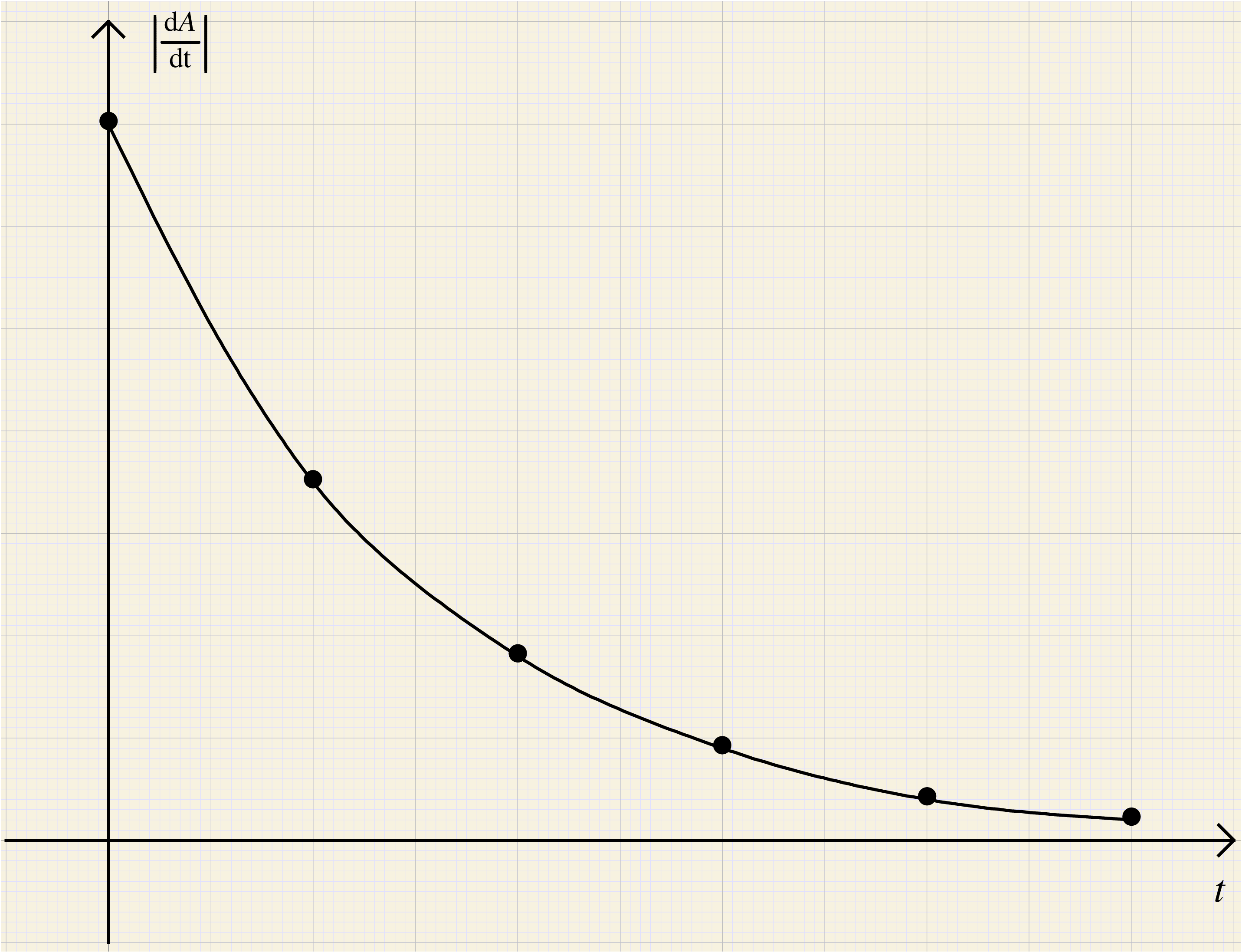
La vitesse de décroissance de l'activité est donc bien
maximale pour 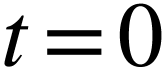et diminue ensuite au cours du
temps.
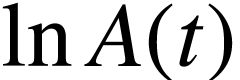pour
déterminer la valeur de ?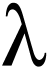
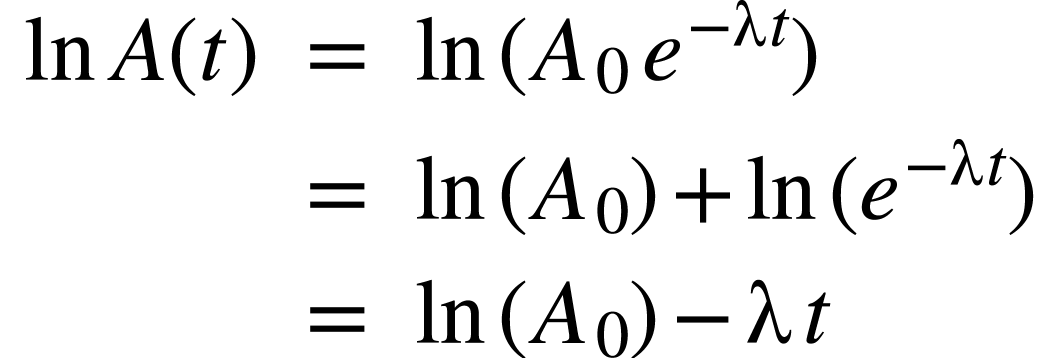
L'évolution de 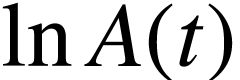est affin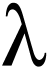e. est la valeur absolue de la pente de la droite, ce qui
n'est pas difficile à déterminer
expérimentalement, une fois la droite tracée.