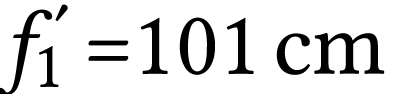 , l'oculaire est
modélisé par une lentille convergente de distance focale
, l'oculaire est
modélisé par une lentille convergente de distance focale
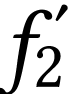 .
.
|
En 1939, les physiciens Pettit et Nicholson ont étudié la température de surface de la Lune à partir de la mesure de la puissance émise par la Lune lors de l'éclipse lunaire du 28 octobre 1939.
Cet exercice décrit une expérience menée au laboratoire pour déterminer la puissance lumineuse surfacique au niveau de la surface de la Terre lors d'une pleine Lune.
On s'intéresse d'abord à un dispositif de détection qui permet de capter la lumière issue de la Lune, puis on étudie un capteur thermique afin de déterminer la puissance lumineuse surfacique rayonnée lors d'une pleine Lune sur le sol terrestre.
Pour déterminer la puissance émise par la Lune, Edison Pettit a placé un capteur de température au foyer du télescope du Mont Wilson.
On reproduit l'expérience de Pettit au laboratoire en utilisant
une lunette afocale. La lumière diffusée par la Lune est
ainsi concentrée sur un capteur de température fixé
au foyer image de l'objectif de la lunette. L'objectif de la lunette est
modélisé par une lentille convergente de distance focale
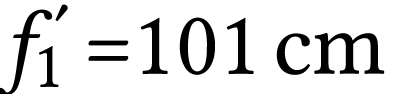 , l'oculaire est
modélisé par une lentille convergente de distance focale
, l'oculaire est
modélisé par une lentille convergente de distance focale
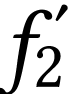 .
.
Le capteur de température se présente sous la forme d'un petit carré noir de 0,8 mm de côté.


Une lunette afocale donne d'un objet à l'infini une image
à l'infini. Le plan focal image de l'objectif doit
coïncider avec le plan focal objet de l'oculaire (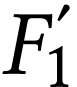 , foyer image de l'objectif, doit donc
coïncider avec
, foyer image de l'objectif, doit donc
coïncider avec 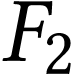 ,
foyer objet de l'oculaire).
,
foyer objet de l'oculaire).
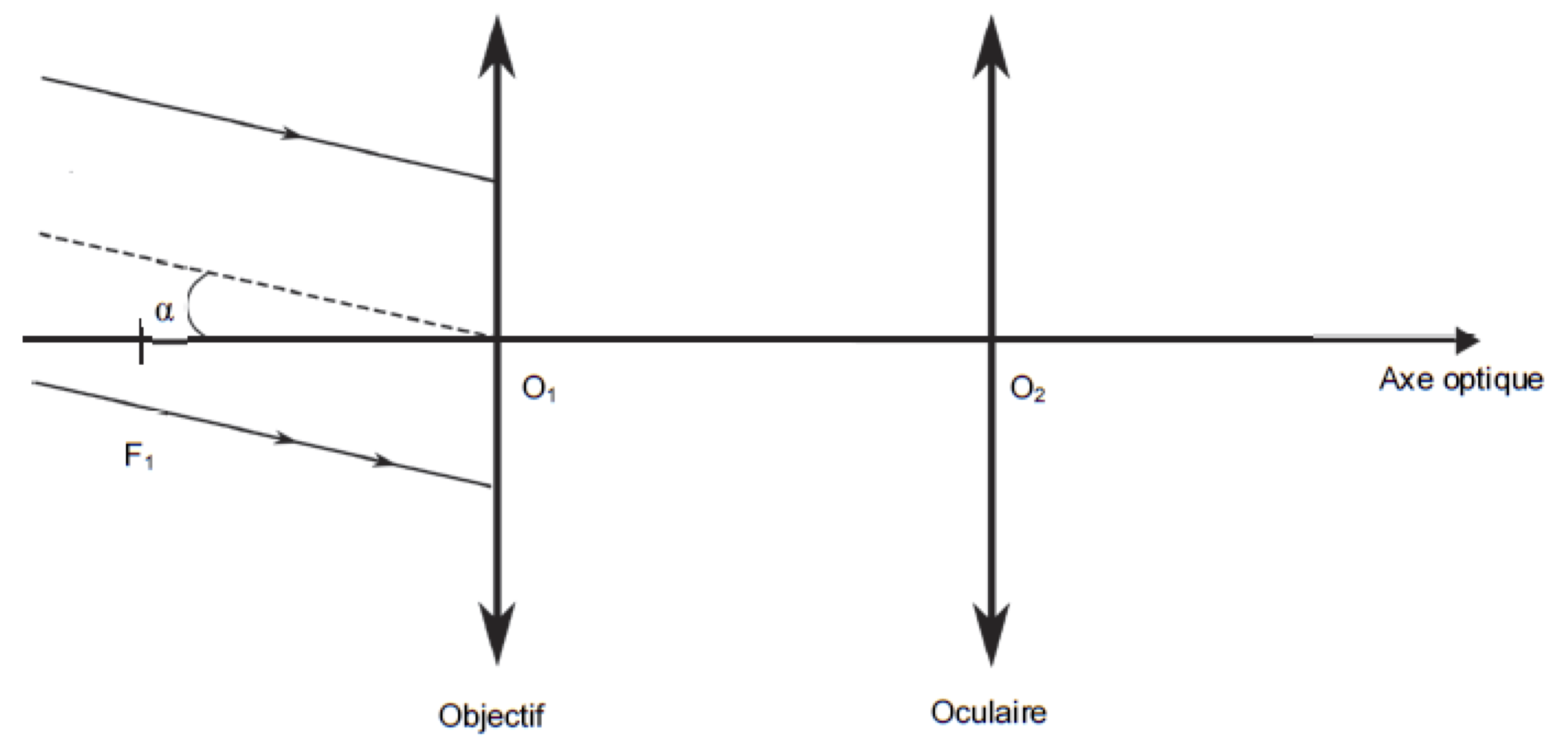


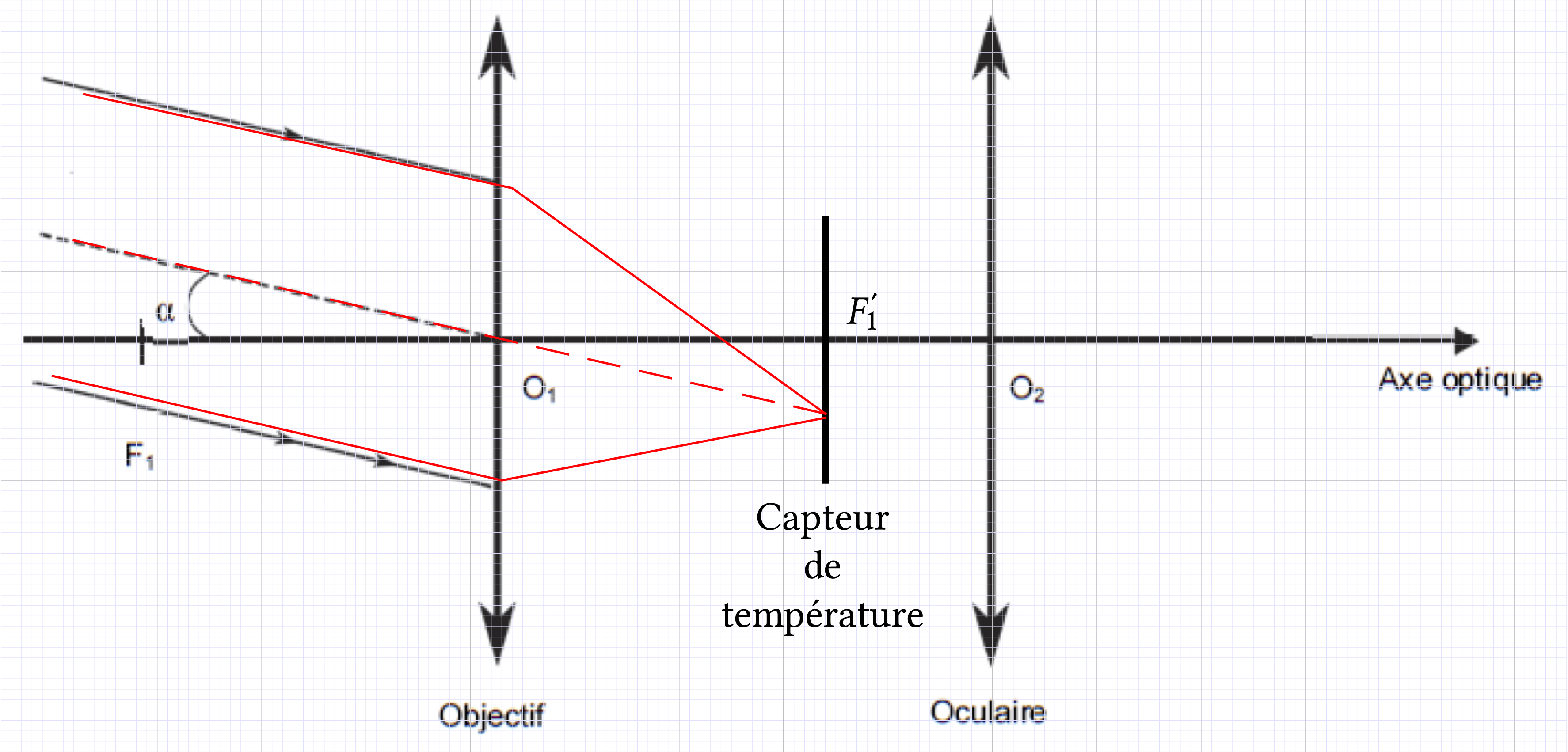
Le capteur de température doit être placé au foyer image de l'objectif.
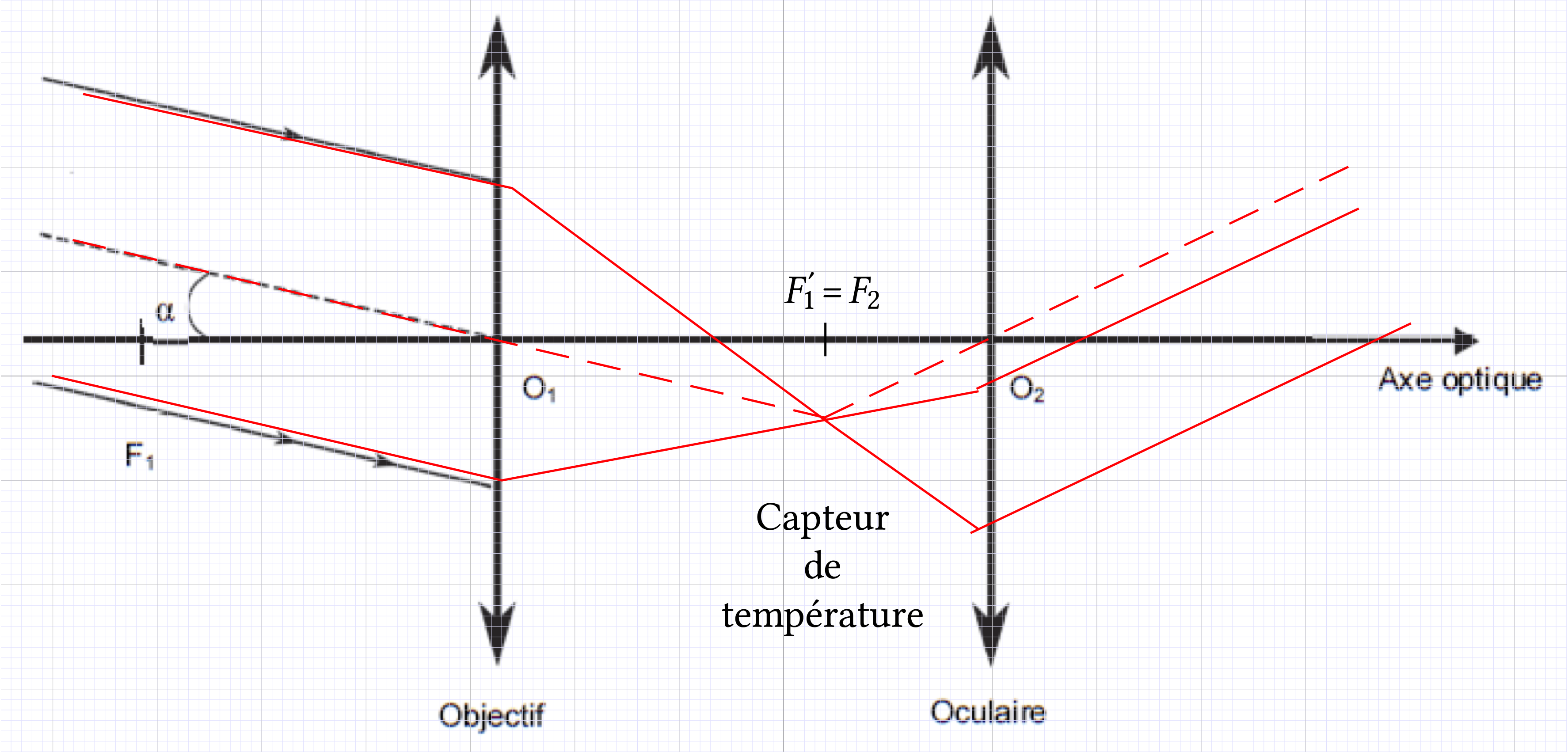
 par rapport à
l'axe optique et traversant la lunette afocale.
par rapport à
l'axe optique et traversant la lunette afocale.


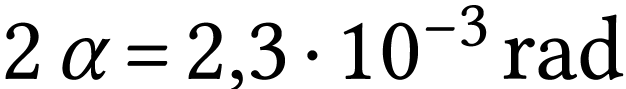 .
.


On étudie maintenant un capteur de température de type
« thermocouple » de capacité thermique  . La température indiquée par ce
capteur peut être reliée à la puissance
rayonnée qu'il reçoit.
. La température indiquée par ce
capteur peut être reliée à la puissance
rayonnée qu'il reçoit.
Pour déterminer la résistance thermique  liée au transfert thermique entre le milieu extérieur et
le capteur, on étudie le comportement au cours du temps du
capteur exposé directement au rayonnement solaire (sans utiliser
la lunette étudiée précédemment).
liée au transfert thermique entre le milieu extérieur et
le capteur, on étudie le comportement au cours du temps du
capteur exposé directement au rayonnement solaire (sans utiliser
la lunette étudiée précédemment).
La température du milieu extérieur dans lequel se trouve
le capteur est supposée constante et notée 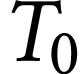 pendant toute la durée de l'expérience.
pendant toute la durée de l'expérience.
L'étude est conduite entre 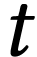 et
et 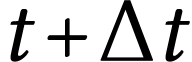 ,
, 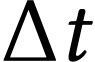 est
supposé petit devant la durée typique de
l'évolution de la température du thermocouple.
est
supposé petit devant la durée typique de
l'évolution de la température du thermocouple.
À l'état initial 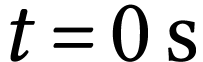 ,
le capteur est dans l'obscurité et à
l'équilibre thermique : sa température est
égale à
,
le capteur est dans l'obscurité et à
l'équilibre thermique : sa température est
égale à 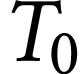 .
.
À 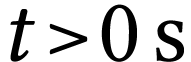 , on expose le
capteur à la lumière du Soleil ce qui fait augmenter
sa température
, on expose le
capteur à la lumière du Soleil ce qui fait augmenter
sa température 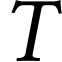 .
On note
.
On note  la puissance lumineuse reçue
par le capteur, elle est supposée constante.
la puissance lumineuse reçue
par le capteur, elle est supposée constante.
Il se produit alors un transfert thermique du capteur de
température 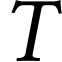 vers le milieu
extérieur de température
vers le milieu
extérieur de température 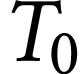 .
.
Dans la suite de l'exercice, le capteur est choisi comme système.
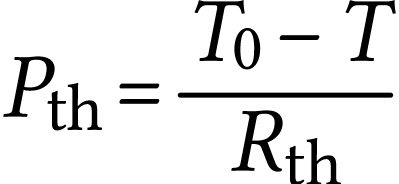
Commenter le signe de cette puissance.


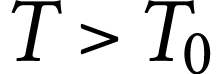 puisque le capteur reçoit de
l'énergie sous forme de rayonnement. On a donc
puisque le capteur reçoit de
l'énergie sous forme de rayonnement. On a donc 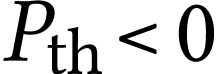 : le système cède de l'énergie
à son environnement.
: le système cède de l'énergie
à son environnement.
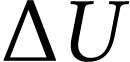 en fonction de sa capacité thermique et de la
variation
en fonction de sa capacité thermique et de la
variation 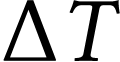 de sa température au cours du
temps
de sa température au cours du
temps 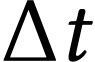 .
.


Pendant la durée 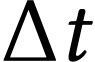 ,
la variation d'énergie interne du capteur a pour expression
,
la variation d'énergie interne du capteur a pour expression
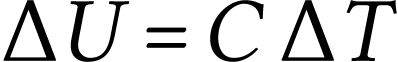 , avec
, avec  la capacité thermique du capteur.
la capacité thermique du capteur.
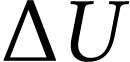 du capteur à la puissance thermique
du capteur à la puissance thermique 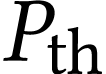 et
à la puissance lumineuse reçue
et
à la puissance lumineuse reçue  pendant une durée
pendant une durée 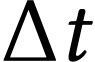 .
.


D'après le premier principe de la thermodynamique, pendant la
durée 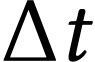 ,
l'énergie interne
,
l'énergie interne 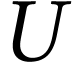 du capteur varie
car il reçoit des transferts d'énergie :
du capteur varie
car il reçoit des transferts d'énergie :
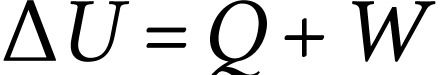
Comme aucune force agissant sur le capteur ne voit son point
d'application bouger, 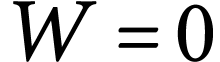 et
et
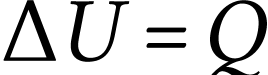
Une puissance 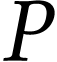 est une énergie
échangée pendant une seconde. Si cette puissance est
constante, l'énergie thermique échangé pendant
est une énergie
échangée pendant une seconde. Si cette puissance est
constante, l'énergie thermique échangé pendant
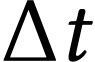 secondes est égale à
secondes est égale à 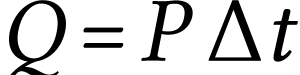 . On en déduit donc que
l'énergie thermique reçue par rayonnement à
pour expression
. On en déduit donc que
l'énergie thermique reçue par rayonnement à
pour expression
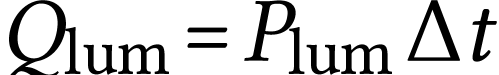
et que celle perdue par conduction a pour expression
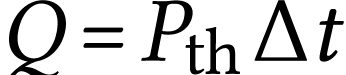
Finalement
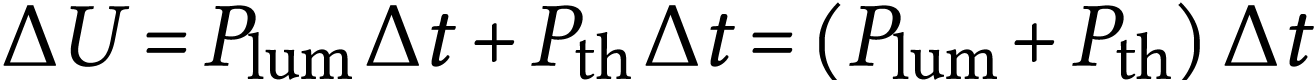
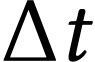 tendant vers 0 que la température
tendant vers 0 que la température 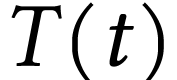 du
capteur de température vérifie l'équation
différentielle suivante :
du
capteur de température vérifie l'équation
différentielle suivante :
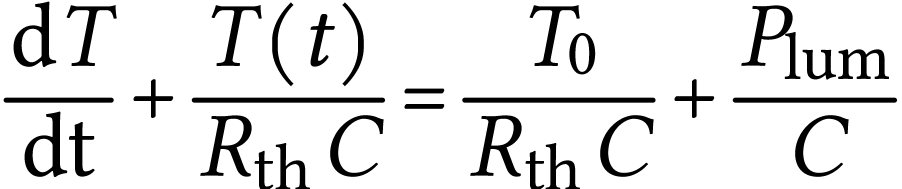


Si on prend en compte les expression des questions 2.3) et 2.4), on
peut écrire, pendant la durée 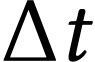 ,
,
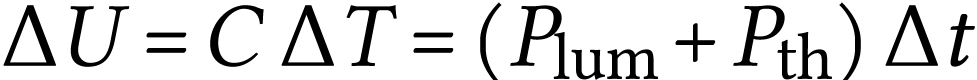
soit

Pour introduire la dérivée, 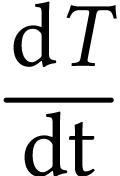 , il suffit de passer à la limite
, il suffit de passer à la limite 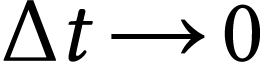 , ce qui n'affecte pas les
termes constants ou celui avec la température
, ce qui n'affecte pas les
termes constants ou celui avec la température
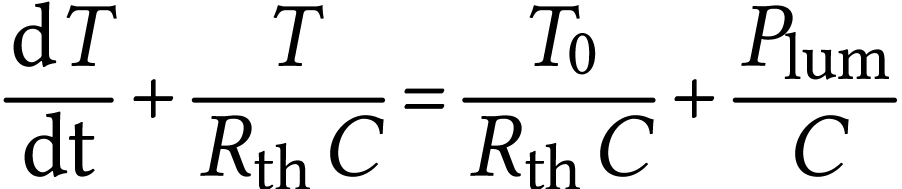
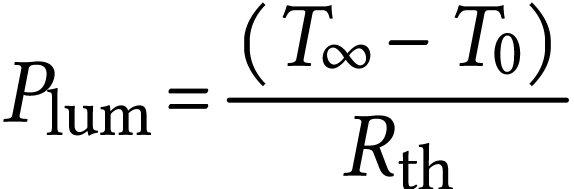
avec 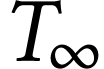 la température finale atteinte par
le capteur.
la température finale atteinte par
le capteur.
Retrouver cette expression à partir de
l'équation différentielle de la question 2.4).


Une grandeur, dont le comportement est régi par une équation différentielle linéraire du premier ordre à coefficient et second membre constants, présente deux comportements : un régime initial variable et un régime final permanent constant.
Si 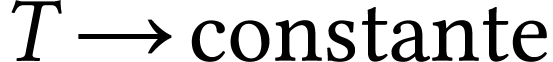 lorsque
lorsque  ,
alors
,
alors 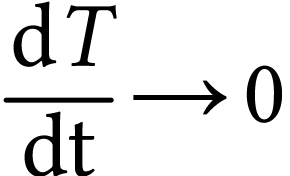 lorsque
lorsque  .
L'équation différentielle s'écrit alors
.
L'équation différentielle s'écrit alors
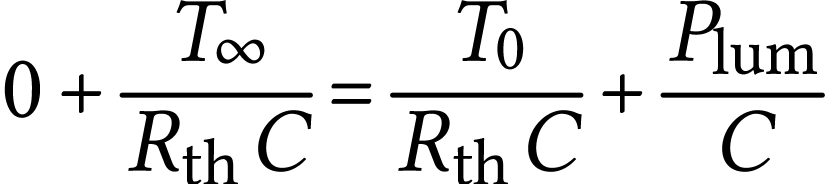
soit
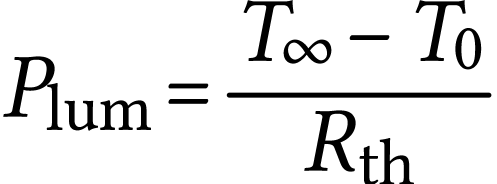
On admet que l'étude expérimentale permet de
déterminer la valeur de la résistance thermique : 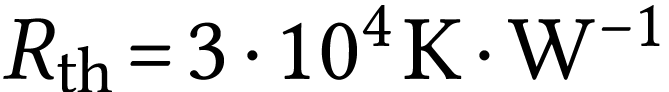 .
.
Pour déterminer la puissance surfacique 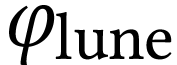 au niveau du sol terrestre lors d'une pleine Lune, on place ce capteur
au foyer image de l'objectif d'une lunette.
au niveau du sol terrestre lors d'une pleine Lune, on place ce capteur
au foyer image de l'objectif d'une lunette.
La puissance  reçue par le capteur est amplifiée d'un
facteur 500 par la lunette utilisée.
reçue par le capteur est amplifiée d'un
facteur 500 par la lunette utilisée.
On relève la
température du capteur au cours du temps. La température
se stabilise au bout de 250 s et on mesure alors 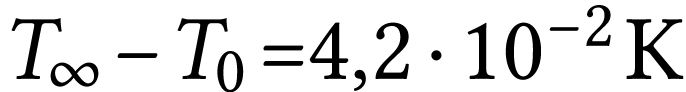 .
.
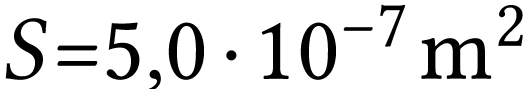 ,
évaluer la puissance surfacique
,
évaluer la puissance surfacique 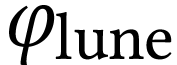 au
niveau du sol terrestre.
au
niveau du sol terrestre.
Comparer ensuite la valeur expérimentale à la puissance
surfacique moyenne obtenue au niveau du sol terrestre lors d'une pleine
Lune : 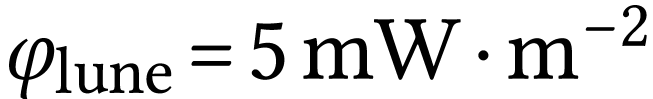 .
.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n'a pas abouti. La démarche est évaluée et nécessite d'être correctement présentée.


À partir des données, on peut calculer  grâce à l'expression
démontrée à la question
précédente.
grâce à l'expression
démontrée à la question
précédente.
En utilisant le facteur d'amplification du à la lunette, on peut calculer la puissance lumineuse qui arrive sur Terre.
Cette puissance est reçue par le capteur de surface 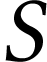 . On peut donc en
déduire la puissance surfacique.
. On peut donc en
déduire la puissance surfacique.
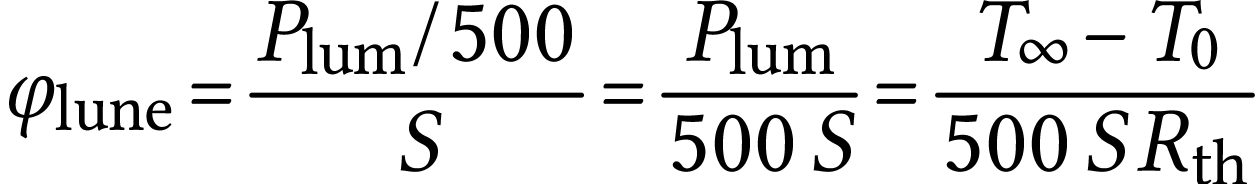
A.N. 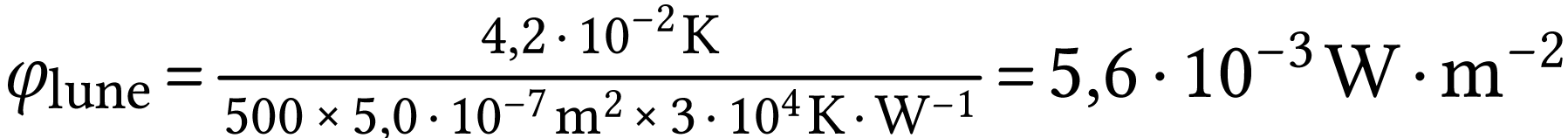 .
.
Cette valeur est proche de celle annoncée.