Un magasin achète des cordes d'escalade de longueur 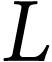 et les découpe (soigneusement) en cordes plus
petites pour les vendre à ses clients. On souhaite
déterminer un découpage optimal pour maximiser le revenu,
sachant que les prix de ventes
et les découpe (soigneusement) en cordes plus
petites pour les vendre à ses clients. On souhaite
déterminer un découpage optimal pour maximiser le revenu,
sachant que les prix de ventes 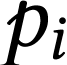 d'une corde de
d'une corde de
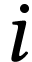 mètres sont donnés.
mètres sont donnés.
Par
exemple, supposons qu'on dispose d'une corde de 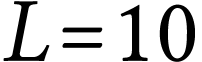 mètres, avec les prix de ventes indiqués dans le tableau
suivant :
mètres, avec les prix de ventes indiqués dans le tableau
suivant :
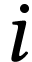 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
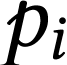 |
0 |
1 |
5 |
8 |
9 |
10 |
17 |
18 |
20 |
24 |
26 |
1Utilisation d'une stratégie
gloutonne
1.
Rappeler en quoi consiste une stratégie gloutonne.

 Réponse
Réponse
Lorsqu'on met en œuvre une stratégie gloutonne, on
cherche, à chaque étape, le meilleur choix « du
moment », c'est à dire un choix optimum local.
2.
On définit la
densité d'une corde de longueur
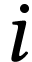
comme étant le rapport
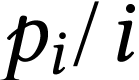 ,
, c'est-à-dire son prix au
mètre. Expliquer en quoi cette grandeur pourrait être
pertinente dans la mise en œuvre d'un algorithme glouton.
Remarque : une grandeur comparable a
été utilisée dans le problème du sac
à dos.

 Réponse
Réponse
Puisqu'on cherche à maximiser le profit, l'idée est de
commencer à découper la corde par les longueurs qui
rapportent le plus à l'instant où l'on effectue la
découpe, c'est à dire les segments dont la
densité est la plus grande.
3.
Quelle instruction mathématique permettrait de
déterminer par combien de segments de longueur
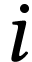
une corde de longueur
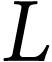
peut être
découpée ?

 Réponse
Réponse
La division entière : 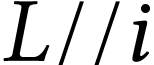
4.
Quelle instruction mathématique permettrait de
déterminer la longueur de corde restante après la
découpe de segments de longueur
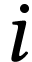
?

 Réponse
Réponse
5.
Écrire le code de la fonction sol_gloutonne
dont la spécification est :
def decoupe_gloutonne(L, s, p):
"""
Détermine grâce à une stratégie gloutonne la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
Paramètres
----------
L : int
Longueur de la corde
s : list[int]
Liste des segments possibles
p : list[int]
Prix associés aux segments
Valeur retournée
----------------
(somme, {segment : nombre})
Tuple formé de la somme gagnée "optimale"
et du dictionnaire des segments de découpe accompagnés de leur nombre.
"""
Utiliser les deux instructions suivantes dans le corps de la fonction
(se renseigner sur l'influence du paramètre key
dans la définition de la fonction sorted) :
donnees = [(s[i], p[i], p[i] / s[i]) for i in range(1, len(s))]
donnees = sorted(donnees, key=lambda donnee: donnee[2])

 Réponse
Réponse
def decoupe_gloutonne(L, s, p):
"""
Détermine grâce à une stratégie gloutonne la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
Paramètres
----------
L : int
Longueur de la corde
s : list[int]
Liste des segments possibles
p : list[int]
Prix associés aux segments
Valeur retournée
----------------
(somme, {segment : nombre})
Tuple formé de la somme gagnée "optimale"
et du dictionnaire des segments de découpe
accompagnés de leur nombre.
"""
# Préparation des données en vue du tri sur la densité
donnees = [(s[i], p[i], p[i] / s[i]) for i in range(1, len(s))]
# Tri des données par densité croissante
donnees = sorted(donnees, key=lambda donnee: donnee[2])
# Valeurs retournées
decoupe = {} # Couples (segment : nbre)
somme = 0
i = 0
while i < len(donnees) and L != 0:
segment = donnees[-1 - i][0]
# Pas la peine de considérer les segments trop grands
if segment <= L:
# Nbre de segments
nbre = L // segment
# Longueur de corde restante
L = L % segment
# Ajout au dictionnaire résultat
decoupe[segment] = nbre
# Ajout à la somme totale
somme += nbre * donnees[-1 - i][1]
i += 1
return (somme, decoupe)
6.
Quel gain peut-on espérer pour une corde de longueur
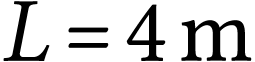
?

 Réponse
Réponse
La stratégie gloutonne nous apprend que l'on peut gagner 9.
2Utilisation de la force brute
Remarque. À partir de cette section on ne
cherche plus à connaître la découpe qui conduit
à la somme maximale. On se contente de chercher cette somme.
7.
On note
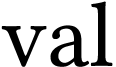
la fonction qui donne la valeur
maximale que l'on peut obtenir en découpant une corde de
longueur
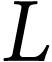 .
. Indiquer la
relation de récurrence que vérifie la fonction
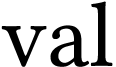 .
.
8.
Écrire le code de la fonction decoupe_force_brute
dont la spécification est :
def decoupe_force_brute(longueur: int,
longueurs: List[int],
prix: List[int]) -> int:
"""
Détermine grâce à une stratégie par force brute la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
"""

 Réponse
Réponse
def decoupe_force_brute(longueur: int,
longueurs: List[int],
prix: List[int]) -> int:
"""
Détermine grâce à une stratégie par force brute la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
"""
if longueur == 0:
return 0
valeur_max = 0
for (i, segment) in enumerate(longueurs):
if longueur - segment >= 0:
valeur_new = prix[i] + decoupe_force_brute(longueur - segment,
longueurs, prix)
if valeur_new > valeur_max:
valeur_max = valeur_new
return valeur_max
9.
Quel gain peut-on espérer pour une corde de longueur
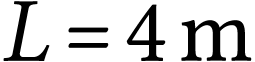
?

 Réponse
Réponse
La stratégie par force brute nous apprend que l'on peut
gagner 10.
3Utilisation de la programmation
dynamique
10.
Rappeler quel est l'objectif de la programmation dynamique.

 Réponse
Réponse
La programmation dynamique est une technique dont le principe
consiste à découper un problème en
sous-problèmes (non indépendants les uns des autres),
à les résoudre et à stocker les
résultats de ces sous-problèmes dans un tableau afin
de les réutiliser.
3.1Utilisation de la
mémoïsation
11.
Que faut-il ajouter au code de la section 2 afin de mettre en
œuvre la mémoïsation ?

 Réponse
Réponse
Il faut utiliser un dictionnaire afin de stocker les
résultats des sous-problèmes rencontrés lors
des apples récursifs.
12.
Écrire le code de la fonction decoupe_memoisation
dont la spécification est :
def decoupe_memoisation(longueur: int, longueurs: List[int],
prix: List[int]) -> int:
"""
Détermine en utilisant la mémoïsation la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
Cette fonction est une fonction enveloppe.
"""

 Réponse
Réponse
def decoupe_memoisation(longueur: int, longueurs: List[int],
prix: List[int]) -> int:
"""
Détermine en utilisant la mémoïsation la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
Cette fonction est une fonction enveloppe.
"""
memo = {0: 0}
def _memoisation(longueur: int, longueurs: List[int], prix: List[int],
memo: Dict[int, int]) -> int:
"""
Fonction qui effectue le traitement.
"""
if longueur not in memo:
valeur_max = 0
for (i, segment) in enumerate(longueurs):
if longueur - segment >= 0:
valeur_new = prix[i] + _memoisation(
longueur - segment, longueurs, prix, memo)
valeur_max = max(valeur_max, valeur_new)
memo[longueur] = valeur_max
return memo[longueur]
_memoisation(longueur, longueurs, prix, memo)
return memo[longueur]
13.
La valeur retournée par la méthode decoupe_memoisation
doit-elle différer de celle retournée par la fonction
decoupe_force_brute ? Pourquoi ?

 Réponse
Réponse
La réponse doit être identique puisque la
mémoïsation ne modifie pas fondamentalement l'algorithme
mais enregistre simplement les calculs intermédiaires de
façon à ne pas avoir à les calculer plusieurs
fois.
3.2Utilisation d'une méthode
tabulaire
14.
Indiquer le principe de la méthode tabulaire.

 Réponse
Réponse
La méthode tabulaire consiste à calculer tous les
sous-problèmes en partant du plus petit jusqu'au
problème recherché.
15.
Quelle structure doit-on ajoute au programme de la section 2 pour
mettre en œuvre la méthode tabulaire ?

 Réponse
Réponse
Il faut utiliser un tableau afin de stocker tous les calculs
intermédiaires, en partant du plus petit
sous-problème.
16.
Écrire le code de la fonction decoupe_tabulaire
dont la spécification est :
def decoupe_tabulaire(longueur: int, longueurs: List[int],
prix: List[int]) -> int:
"""
Détermine en utilisant la méthode tabulaire la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
"""

 Réponse
Réponse
def decoupe_tabulaire(longueur: int, longueurs: List[int],
prix: List[int]) -> int:
"""
Détermine en utilisant la méthode tabulaire la découpe optimale
d une corde, connaissant les longueurs des segments possibles
et les valeurs associées.
"""
valeurs = [0 for i in range(longueur + 1)]
for long in range(longueur + 1):
if long == 0:
valeurs[long] = 0
else:
for i, segment in enumerate(longueurs):
if long - segment >= 0:
valeur = prix[i] + valeurs[long - (i + 1)]
if valeur > valeurs[long]:
valeurs[long] = valeur
return valeurs[longueur]
17.
La valeur retournée par la méthode decoupe_tabulaire
doit-elle différer de celle retournée par la fonction
decoupe_force_brute ? Pourquoi ?

 Réponse
Réponse
La réponse doit être identique puisque la
méthode tabulaire ne modifie pas fondamentalement
l'algorithme mais enregistre simplement les calculs
intermédiaires de façon à ne pas avoir à
les calculer plusieurs fois.
4Correction
La correction se trouve à cette adresse.
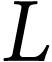 et les découpe (soigneusement) en cordes plus
petites pour les vendre à ses clients. On souhaite
déterminer un découpage optimal pour maximiser le revenu,
sachant que les prix de ventes
et les découpe (soigneusement) en cordes plus
petites pour les vendre à ses clients. On souhaite
déterminer un découpage optimal pour maximiser le revenu,
sachant que les prix de ventes 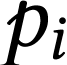 d'une corde de
d'une corde de
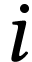 mètres sont donnés.
mètres sont donnés.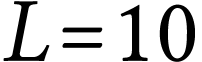 mètres, avec les prix de ventes indiqués dans le tableau
suivant :
mètres, avec les prix de ventes indiqués dans le tableau
suivant :


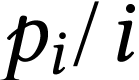 ,
,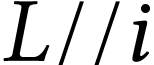
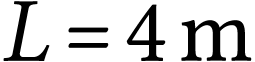 ?
?
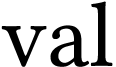 la fonction qui donne la valeur
maximale que l'on peut obtenir en découpant une corde de
longueur
la fonction qui donne la valeur
maximale que l'on peut obtenir en découpant une corde de
longueur 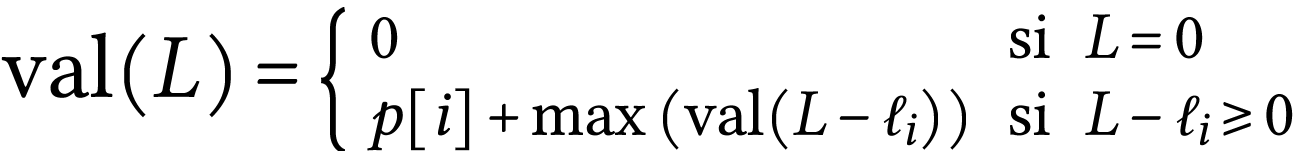
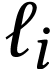 est l'un des segments possibles et
est l'un des segments possibles et
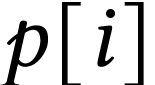 le prix associé.
le prix associé.