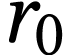Satellite et frottements

Un satellite est placé sur une orbite circulaire de rayon 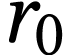contenue dans le plan équatorial.

Remarque. L'énergie potentielle gravitationnelle d'un système {satellite + Terre} a pour expression :

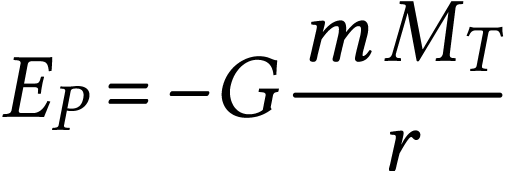
où est la constante d'attraction universelle, 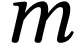la masse du satellite, 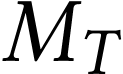la masse de la Terre et 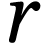la distance du satellite au centre de la Terre.

1)
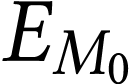Déterminer l'expression de l'énergie mécanique en fonction de , , 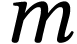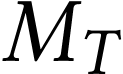et .
On travaille dans le référentiel géocentrique supposé galiléen, la Terre est immobile.

Réponse

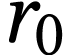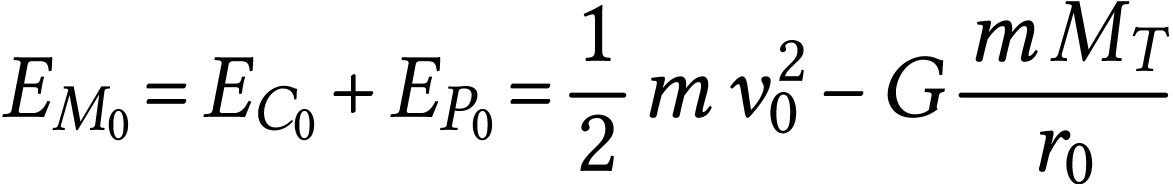
Le mouvement étant circulaire, on montre dans le cours qu'il est uniforme et que

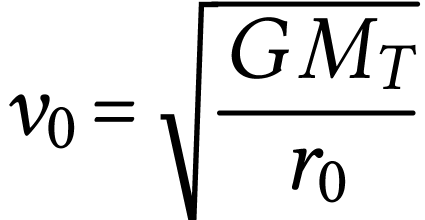
donc

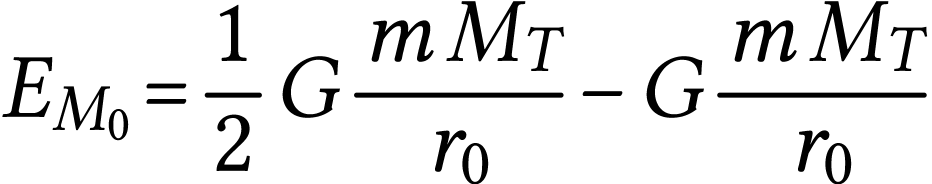
Finalement

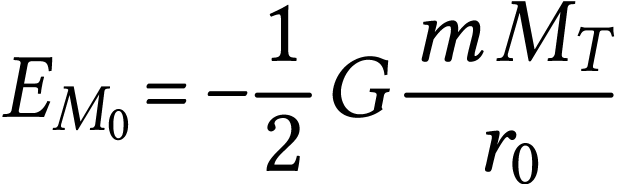
L'altitude du satellite étant peu élevée, il subit les frottements des hautes couches de l'atmosphère. Son énergie mécanique totale diminue alors avec le temps suivant la loi :

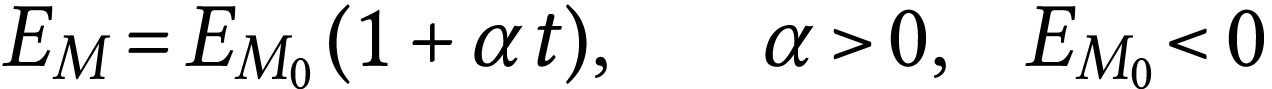
On suppose que la trajectoire reste circulaire.

2)
Déterminer, en fonction du temps, le rayon de la trajectoire du satellite.

Réponse

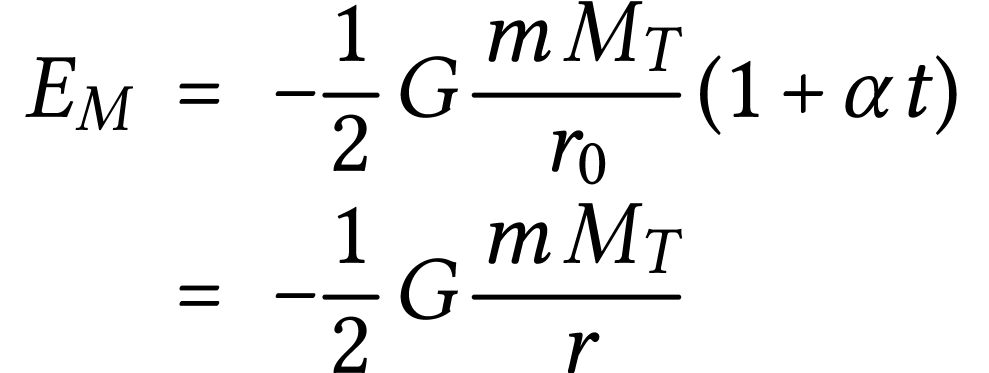
puisqu'on suppose que la trajectoire reste un cercle, même lorsque 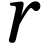varie.
Finalement,

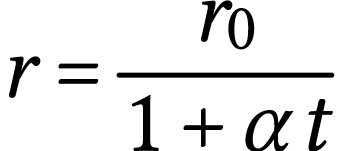
Le rayon diminue bien avec le temps.

3)
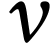Déterminer, en fonction du temps, la vitesse du satellite.

Réponse

À partir de la question 1), on constate que

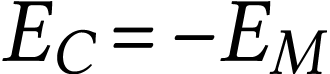
donc

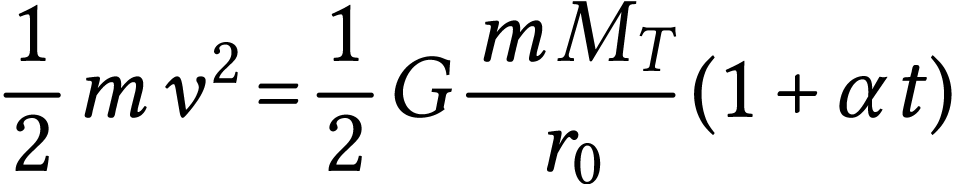
ou

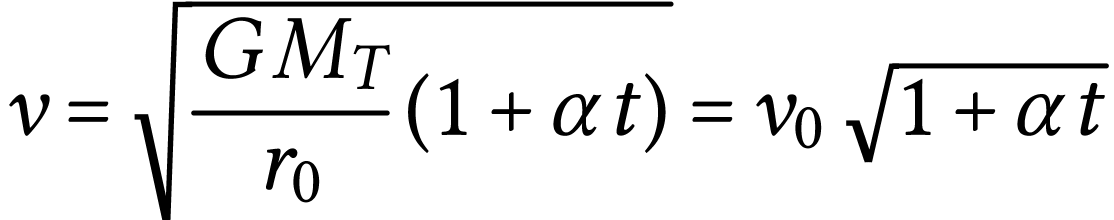
On constate donc que , la vitesse du satellite augmente.

4)
En comparant les énergies, expliquer pourquoi la vitesse du satellite augmente alors qu'il est freiné par l'atmosphère.

Réponse

L'énergie cinétique augmente mais l'énergie potentielle gravitationnelle diminue plus rapidement.